
- •Диф рівняння
- •1: Теорема про існування та єдиність розв’язку задачі Коші диференціального рівняння першого порядку.
- •1. Диференціальні рівняння першого порядку.
- •Теорема про існування та єдиність розв’язку задачі Коші диференціального рівняння першого порядку, що розв’язане відносно похідної.
- •2. Лінійні однорідні диференціальні рівняння з сталими коефіцієнтами. Побудова загального розв’язку.
- •Лінійні однорідні рівняння з сталими коефіцієнтами
- •3. Знаходження частинного розв’язку лінійного неоднорідного рівняння n-го порядку за допомогою методу варіації довільної сталої. Лінійні неоднорідні диференціальні рівняння
- •3.2.1. Властивості розв’язків лінійних неоднорідних рівнянь. Загальний розв’язок лінійного неоднорідного рівняння
- •Теорема про загальний розв’язок лінійного неоднорідного диференціального рівняння.
- •Метод варіації довільної сталої побудови частинного розв’язку лінійного неоднорідного диференціального рівняння
- •4. Системи лінійних диференціальних рівнянь з сталими коефіціентами . Знаходження загального розв’язку однорідних систем. Загальна теорія
- •4.2.1. Властивості розв’язків лінійних однорідних систем
- •Теорема про загальний розв’язок систем лінійних однорідних диференціальних рівнянь.
- •Системи лінійних однорідних диференціальних рівнянь з сталими коефіцієнтами. Метод Ейлера. Системи лінійних однорідних диференціальних рівнянь з сталими коефіцієнтами.
- •4.3.1. Розв’язування систем однорідних рівнянь з сталими коефіцієнтами методом Ейлера.
- •Матричний метод розв’язку лінійних однорідних систем з сталими коефіцієнтами. Розв’язок систем однорідних рівнянь зі сталими коефіцієнтами матричним методом
- •5.Представлення розв’язку лінійних неоднорідних систем за допомогою формули Коши. Лінійні неоднорідні системи
- •Властивості розв’язків лінійних неоднорідних систем
- •Теорема про загальний розв’язок систем лінійних неоднорідних диференціальних рівнянь.
- •Метод варіації довільної сталої знаходження частинного розв’язку лінійних неоднорідних систем. Формула Коші. Побудова частинного розв’язку неоднорідної системи методом варіації довільних сталих
- •Формула Коші
- •6.Теорія стійкості. Стійкість лінійних стаціонарних систем. Критерій Гурвіца. Теорія стійкості руху
- •Фазовий портрет лінійної системи на площині
- •7.Метод функцій Ляпунова. Основні визначення та теореми Другий метод Ляпунова
- •Основні визначення
- •Методи побудови функції Ляпунова
4.3.1. Розв’язування систем однорідних рівнянь з сталими коефіцієнтами методом Ейлера.
Розглянемо
один з методів побудови розв’язку
систем з сталими коефіцієнтами. Розв’язок
системи шукаємо у вигляді вектора
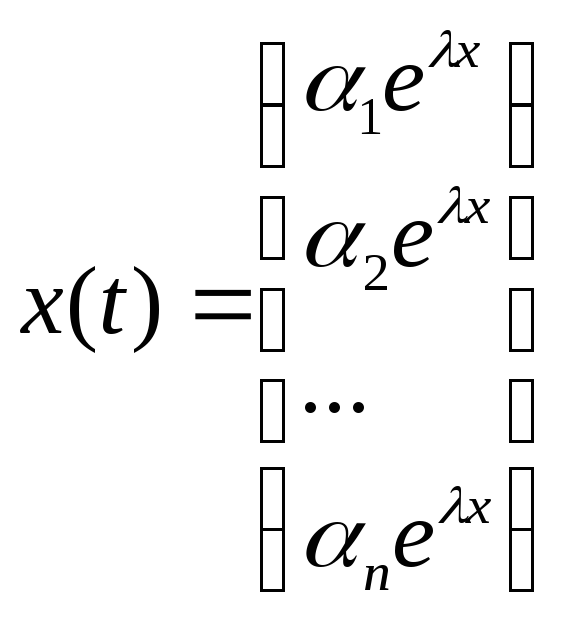 .
Підставивши в систему диференціальних
рівнянь, одержимо
.
Підставивши в систему диференціальних
рівнянь, одержимо
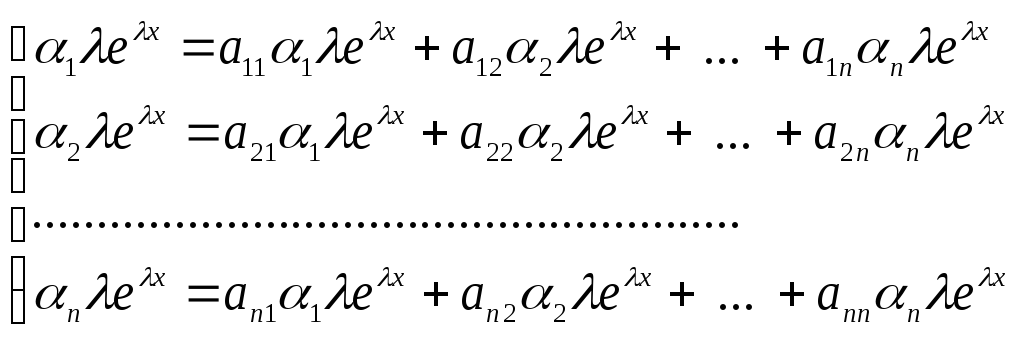 Скоротивши
на
Скоротивши
на
![]() ,
і перенісши всі члени вправо, запишемо
,
і перенісши всі члени вправо, запишемо
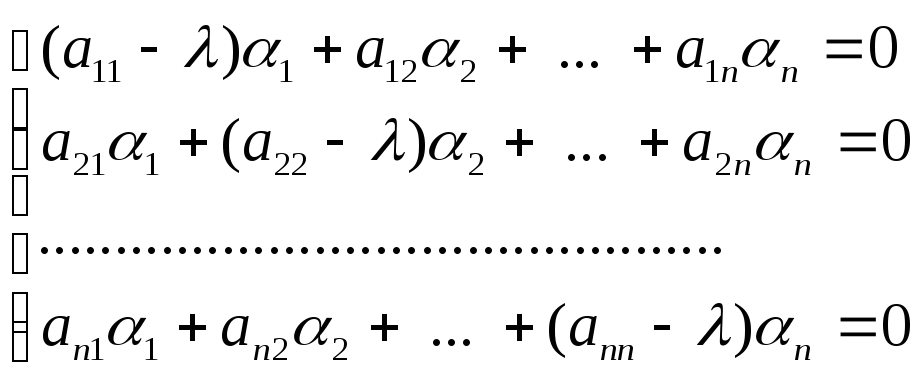 Отримана
однорідна система лінійних алгебраїчних
рівнянь має розв’язок тоді і тільки
тоді, коли її визначник дорівнює нулю,
тобто
Отримана
однорідна система лінійних алгебраїчних
рівнянь має розв’язок тоді і тільки
тоді, коли її визначник дорівнює нулю,
тобто
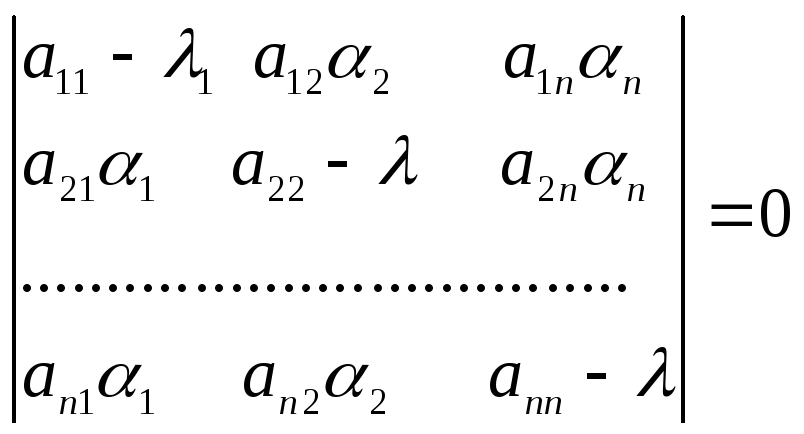 .Це рівняння, може бути записаним у
векторно-матричній формі
.Це рівняння, може бути записаним у
векторно-матричній формі
![]() і воно називається
характеристичним (чи віковим) рівнянням.
Розкриємо його
і воно називається
характеристичним (чи віковим) рівнянням.
Розкриємо його
![]() .
Алгебраїчне рівняння
.
Алгебраїчне рівняння
![]() -го
ступеня має
-го
ступеня має
![]() -коренів.
Розглянемо різні випадки.
-коренів.
Розглянемо різні випадки.
1.
Всі корені характеристичного рівняння
![]() (власні числа матриці
(власні числа матриці
![]() )
дійсні і різні. Підставляючи їх по черзі
в систему алгебраїчних рівнянь
)
дійсні і різні. Підставляючи їх по черзі
в систему алгебраїчних рівнянь
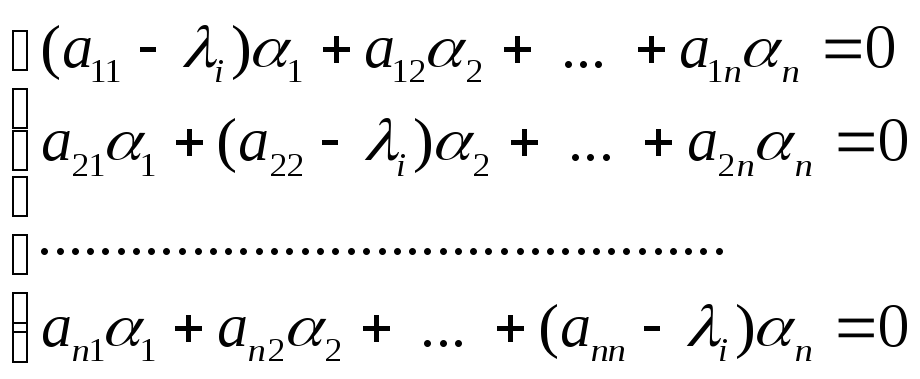 , ненульові розв’язки системи
, ненульові розв’язки системи
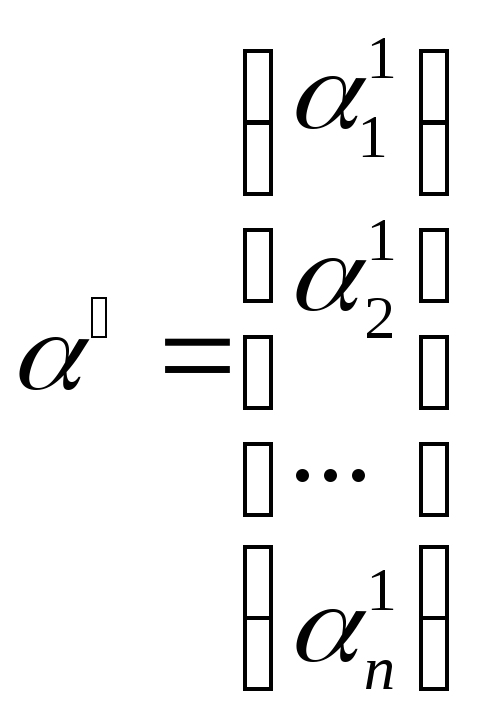 ,
,
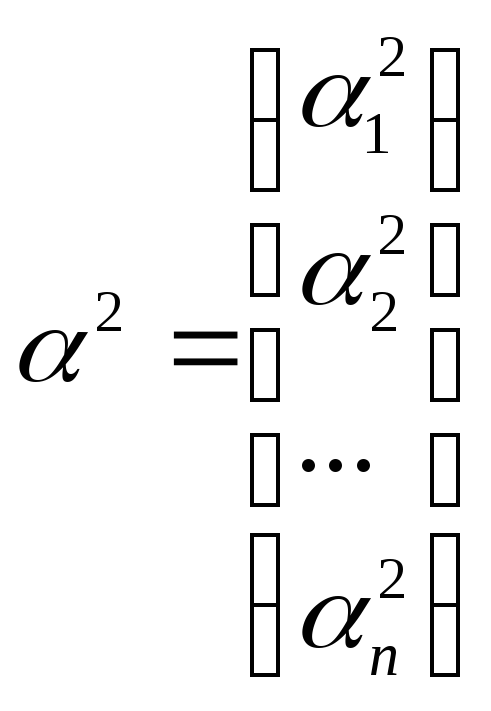 ,
… ,
,
… ,
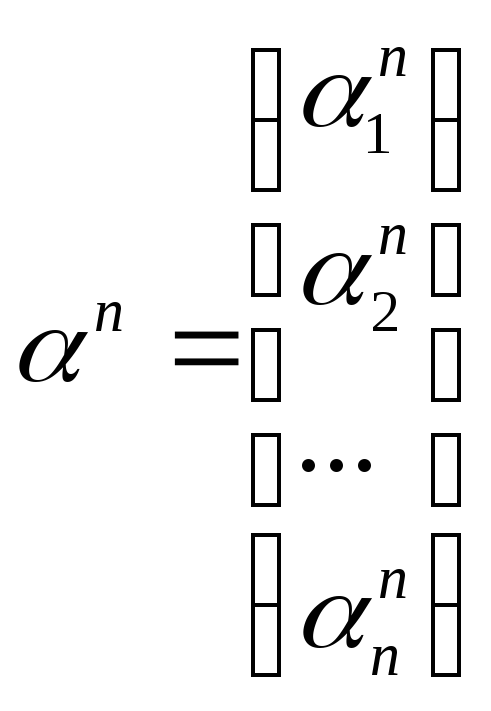 що являють собою власні вектори, які
відповідають власним числам
що являють собою власні вектори, які
відповідають власним числам
![]() ,
,
![]() .
.
У
такий спосіб одержимо
![]() -
розв’язків
-
розв’язків
 ,
,
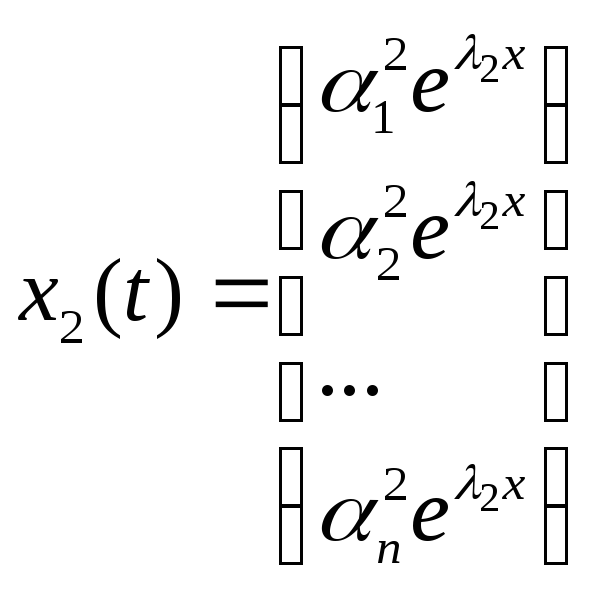 ,
… ,
,
… ,
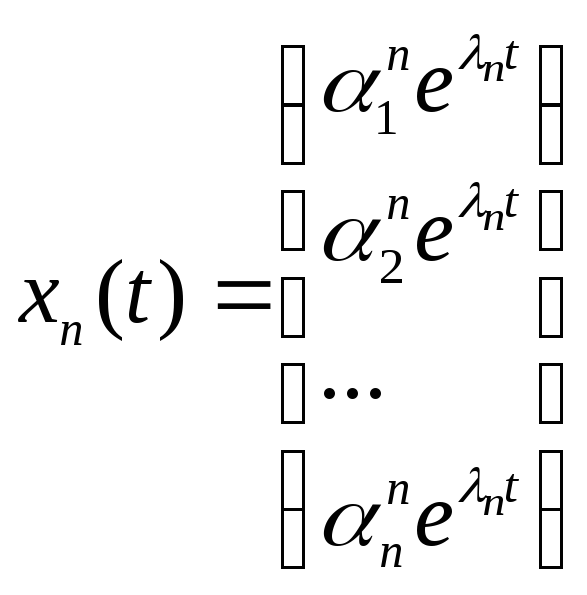 ...
...
Причому
оскільки
![]() -різні
а
-різні
а
![]() -
відповідні їм власні вектори, то розв’язки
-
відповідні їм власні вектори, то розв’язки
![]() -
лінійно незалежні, і загальний розв’язок
системи має вигляд
-
лінійно незалежні, і загальний розв’язок
системи має вигляд
![]() .
Або у векторно - матричної формі запису
.
Або у векторно - матричної формі запису
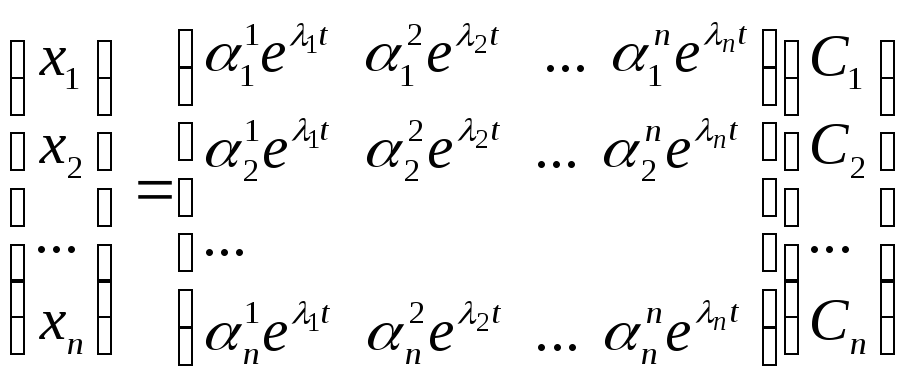 , де
, де
![]() -
довільні сталі.
-
довільні сталі.
2.
Нехай
![]() пара комплексно спряжених коренів.
Візьмемо один з них, наприклад
пара комплексно спряжених коренів.
Візьмемо один з них, наприклад
![]() .
Комплексному власному
числу відповідає комплексний власний
вектор
.
Комплексному власному
числу відповідає комплексний власний
вектор
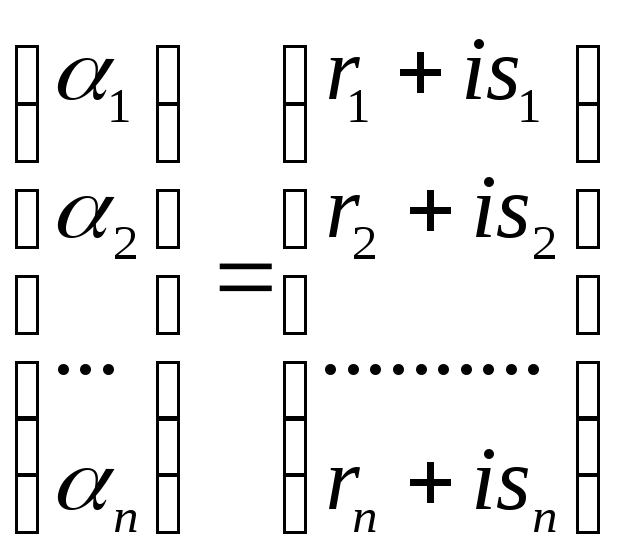 і,
відповідно, розв’язок
і,
відповідно, розв’язок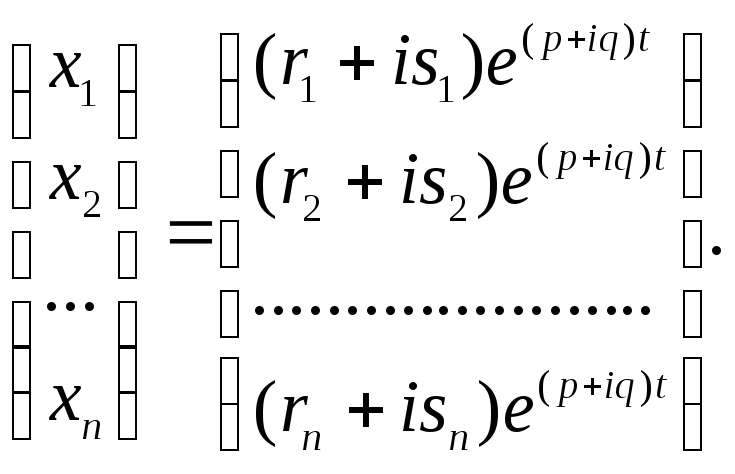
Використовуючи
залежність
![]() ,
перетворимо розв’язок до вигляду:
,
перетворимо розв’язок до вигляду:

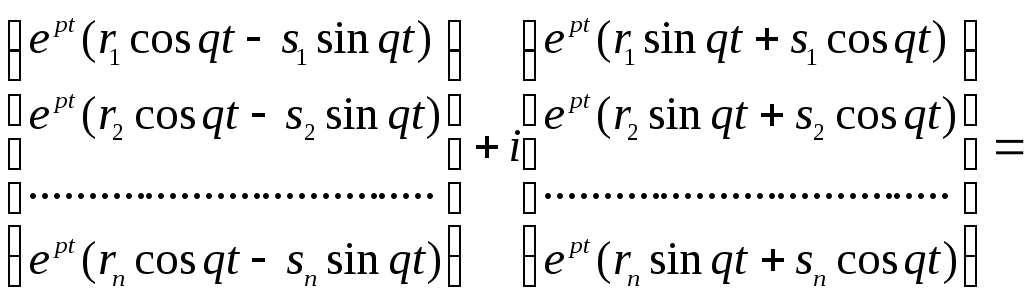
![]()
.
І,
як випливає з властивості 4 розв’язків
однорідних систем, якщо комплексна
функція
![]() дійсного
аргументу є розв’язком однорідної
системи, то окремо дійсна і уявна частини
також будуть розв’язками, тобто
комплексним власним числам
дійсного
аргументу є розв’язком однорідної
системи, то окремо дійсна і уявна частини
також будуть розв’язками, тобто
комплексним власним числам
![]() відповідають лінійно незалежні розв’язки
відповідають лінійно незалежні розв’язки
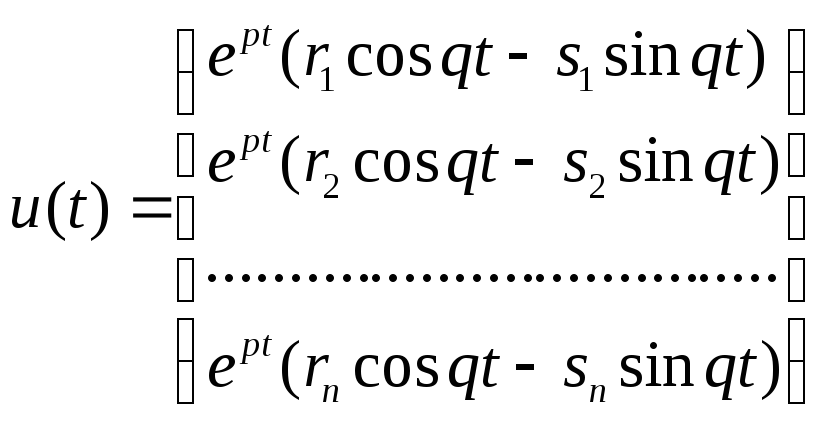 ,
,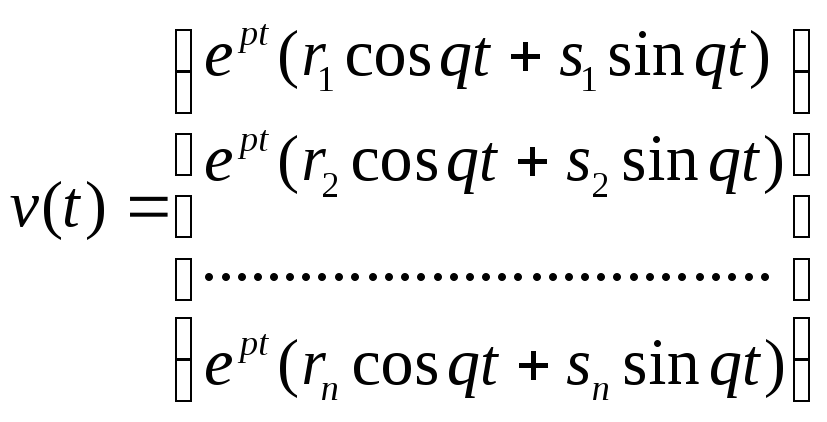 .
.
-
Якщо характеристичне рівняння має кратний корінь
 кратності
кратності
 ,
тобто
,
тобто
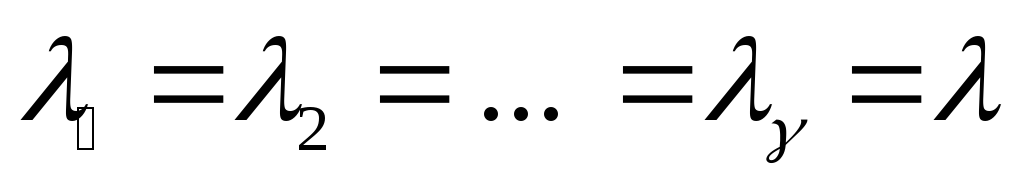 ,
то розв’язок системи рівнянь має вигляд
,
то розв’язок системи рівнянь має вигляд
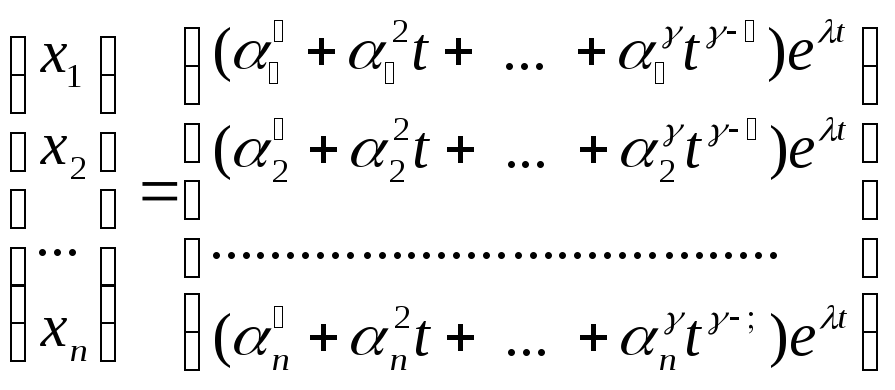 .
Підставивши його у вихідне диференціальне
рівняння і прирівнявши коефіцієнти
при однакових степенях, одержимо
.
Підставивши його у вихідне диференціальне
рівняння і прирівнявши коефіцієнти
при однакових степенях, одержимо
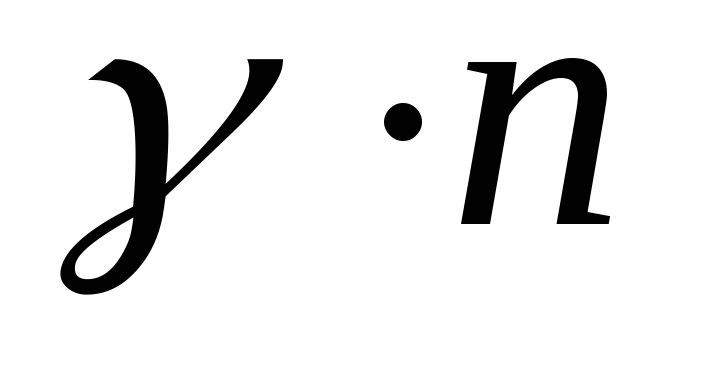 - рівнянь, що містять
- рівнянь, що містять
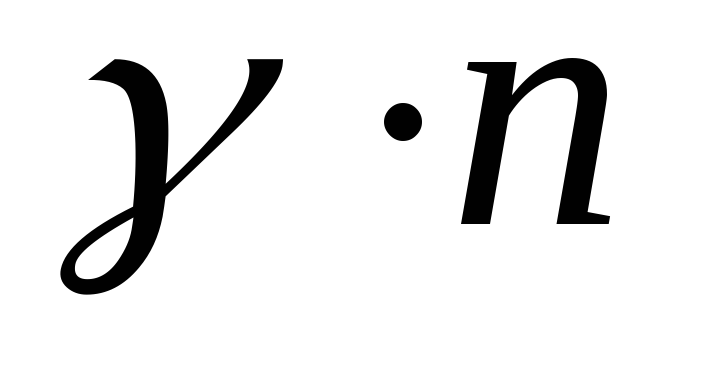 -невідомих.
Тому що корінь характеристичного
рівняння
-невідомих.
Тому що корінь характеристичного
рівняння
 має кратність
має кратність
 ,
то ранг отриманої системи
,
то ранг отриманої системи
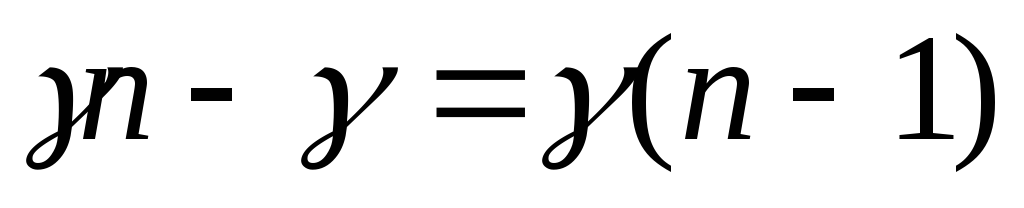 .
Уводячи
.
Уводячи
 довільних сталих
довільних сталих
 і розв’язуючи систему, одержимо
і розв’язуючи систему, одержимо
 ,
,
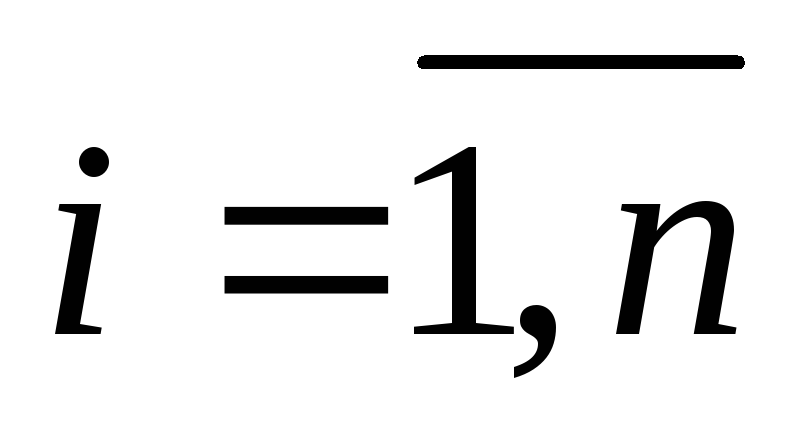 ,
,
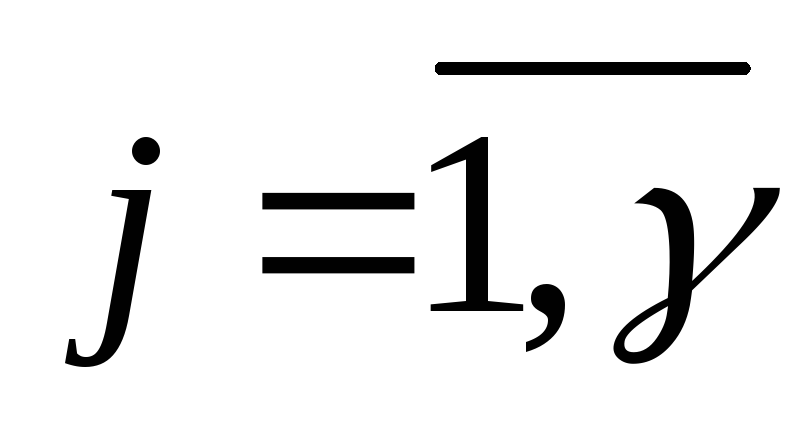 .
.
Матричний метод розв’язку лінійних однорідних систем з сталими коефіцієнтами. Розв’язок систем однорідних рівнянь зі сталими коефіцієнтами матричним методом
Досить
універсальним методом розв’язку
лінійних однорідних систем з сталими
коефіцієнтами є матричний метод. Він
полягає в наступному. Розглядається
лінійна система з сталими коефіцієнтами,
що записана у векторно-матричному
вигляді
![]() .
Робиться невироджене перетворення
.
Робиться невироджене перетворення
![]() ,
де вектор
,
де вектор
![]() - нова невідома векторна функція. Тоді
рівняння прийме вигляд
- нова невідома векторна функція. Тоді
рівняння прийме вигляд
![]() або
або
![]() .
Для довільної матриці
.
Для довільної матриці
![]() завжди існує неособлива матриця
завжди існує неособлива матриця
![]() ,
що приводить її до жорданової форми,
тобто
,
що приводить її до жорданової форми,
тобто
![]() ,
де
,
де
![]() -
жорданова форма матриці
-
жорданова форма матриці
![]() .
І система диференціальних рівнянь
прийме вигляд
.
І система диференціальних рівнянь
прийме вигляд
![]() .
Складемо характеристичне рівняння
матриці
.
Складемо характеристичне рівняння
матриці
![]() :
:
![]() , або
, або
![]() .
Алгебраїчне рівняння
.
Алгебраїчне рівняння
![]() -го
ступеня має
-го
ступеня має
![]() коренів. Розглянемо різні випадки.
коренів. Розглянемо різні випадки.
1.
Нехай
![]() -
дійсні різні числа. Тоді матриця
-
дійсні різні числа. Тоді матриця
![]() має вигляд
має вигляд
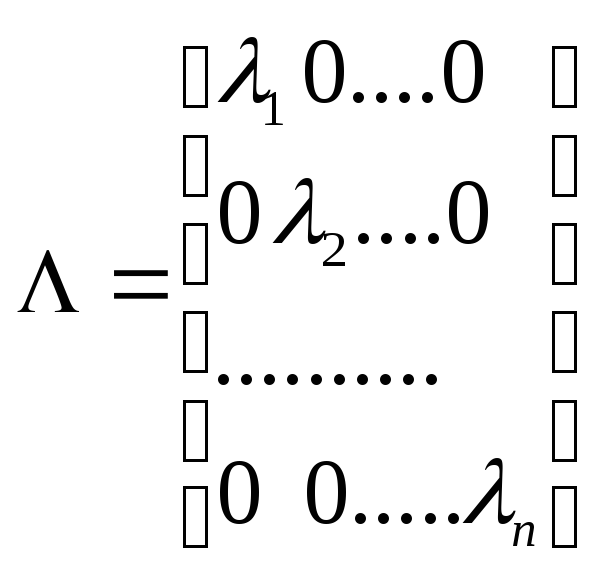 .
І перетворена система диференціальних
рівнянь розпадається на
.
І перетворена система диференціальних
рівнянь розпадається на
![]() - незалежних рівнянь
- незалежних рівнянь
![]() .
.
Розв’язуючи
кожне окремо, отримаємо
![]() .
Або в матричному вигляді
.
Або в матричному вигляді
![]() де
де
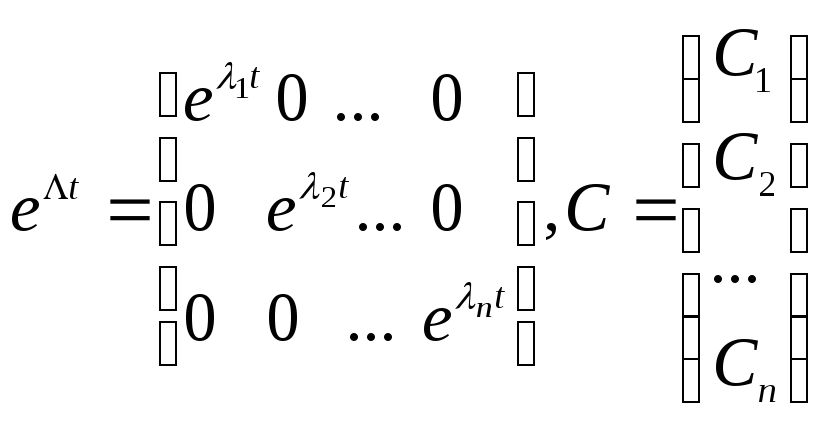 .
Звідси розв’язок вихідного рівняння
має вигляд
.
Звідси розв’язок вихідного рівняння
має вигляд
![]() .
Для знаходження матриці
.
Для знаходження матриці
![]() треба розв’язати матричне рівняння
треба розв’язати матричне рівняння
![]() або
або
![]() ,
де
,
де
![]() - жорданова форма матриці
- жорданова форма матриці
![]() .
Якщо матрицю
.
Якщо матрицю
![]() записати у вигляді
записати у вигляді
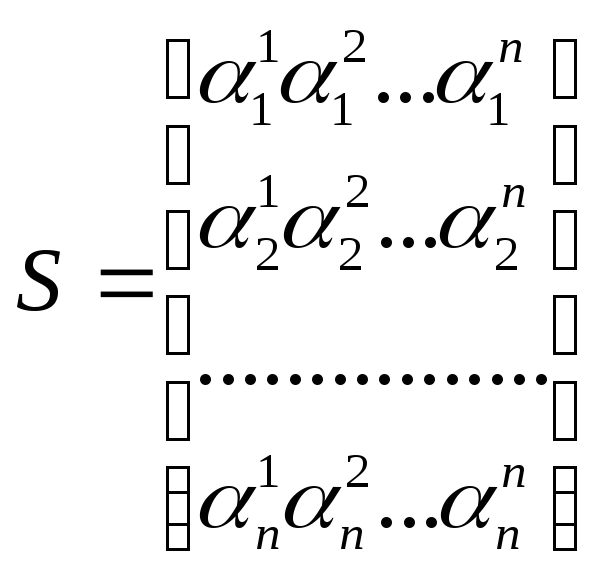 ,
то для кожного з стовпчиків
,
то для кожного з стовпчиків
![]() ,
матричне рівняння перетвориться до
,
матричне рівняння перетвориться до
![]() ,
,
![]() .
Таким чином, у випадку різних дійсних
власних чисел матриця
.
Таким чином, у випадку різних дійсних
власних чисел матриця
![]() являє собою набір
являє собою набір
![]() - власних векторів, що відповідають
різним власним числам.
- власних векторів, що відповідають
різним власним числам.
2.
Нехай
![]() -
комплексний корінь. Тоді відповідна
клітка Жордана має вигляд
-
комплексний корінь. Тоді відповідна
клітка Жордана має вигляд
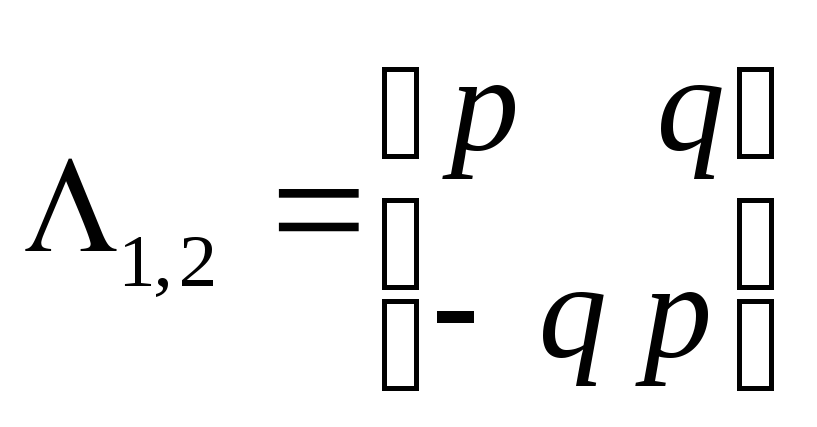 ,
,
а
перетворена система диференціальних
рівнянь
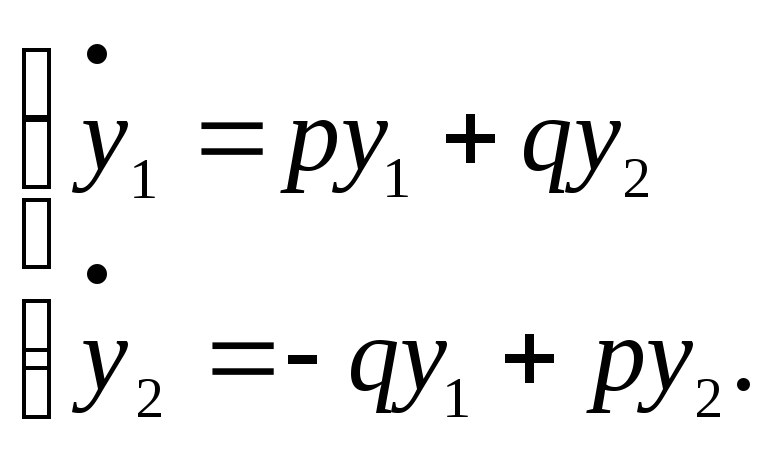 Неважко перевірити,
що розв’язок отриманої системи
диференціальних рівнянь має вигляд
Неважко перевірити,
що розв’язок отриманої системи
диференціальних рівнянь має вигляд
![]()
Або
в матричному вигляді
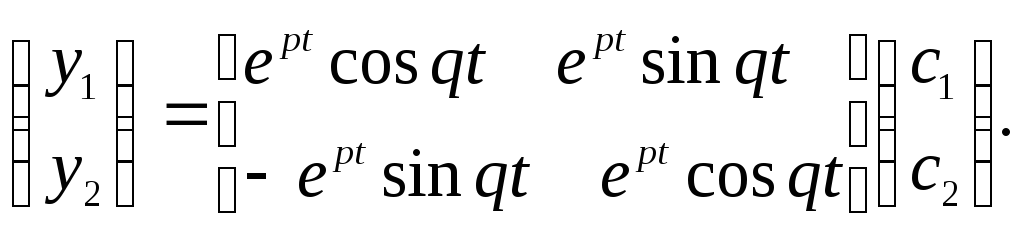 Таким чином,
комплексно-спряженим власним числам
Таким чином,
комплексно-спряженим власним числам
![]() відповідає
розв’язок
відповідає
розв’язок
![]() де
де

3.
Нехай
![]() -
кратний корінь, кратності
-
кратний корінь, кратності
![]() ,
тобто
,
тобто
![]() і йому відповідають
і йому відповідають
![]() лінійно незалежних векторів. Тоді клітка
Жордана, що відповідає цьому власному
числу, має вид
лінійно незалежних векторів. Тоді клітка
Жордана, що відповідає цьому власному
числу, має вид

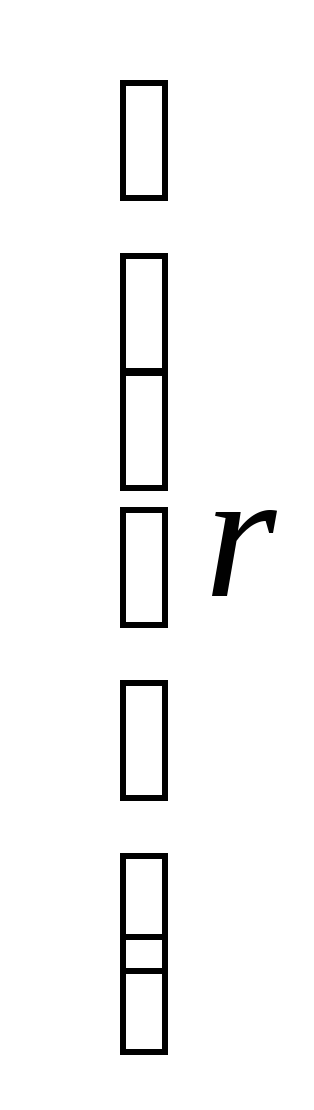
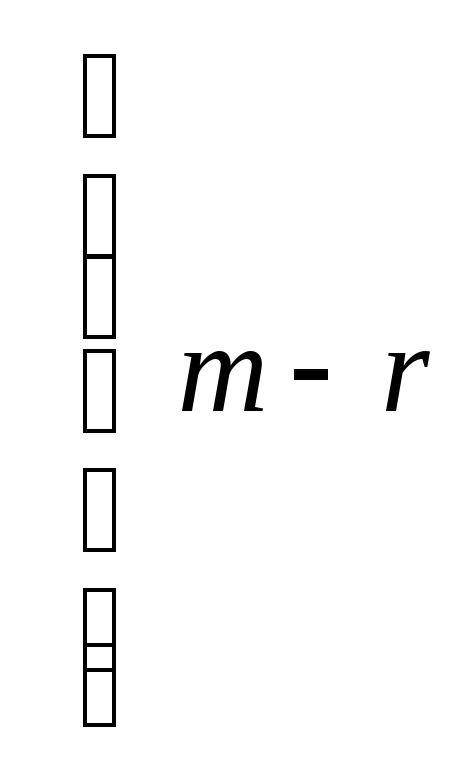
І
перетворена підсистема, що відповідає
власному числу
![]() ,
розпадається не дві підсистеми
,
розпадається не дві підсистеми
![]() .
.
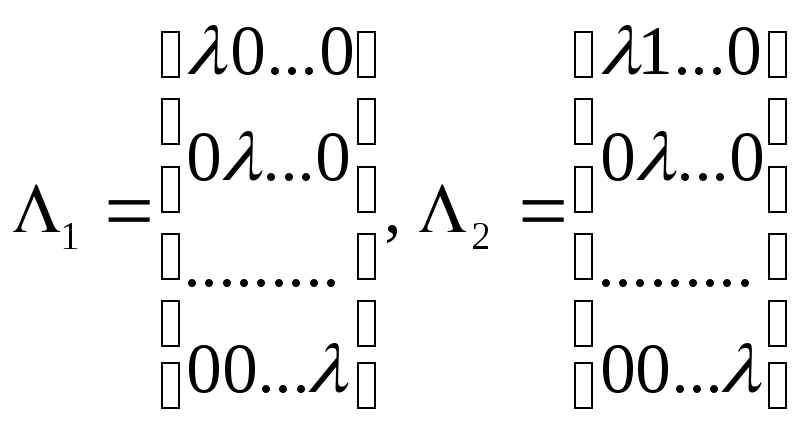 .
Розв’язок першої знаходиться з
використанням зазначеного в першому
пункті підходу. Розглянемо другу
підсистему. Запишемо її в координатному
вигляді
.
Розв’язок першої знаходиться з
використанням зазначеного в першому
пункті підходу. Розглянемо другу
підсистему. Запишемо її в координатному
вигляді
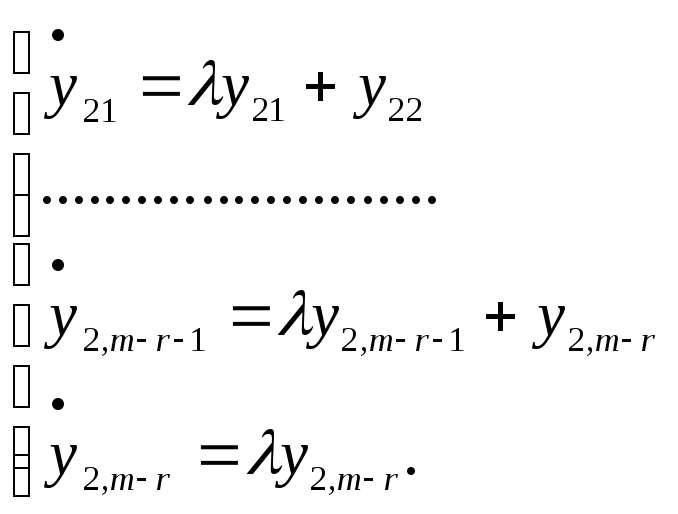 Розв’язок останнього
рівняння цієї підсистеми має вигляд
Розв’язок останнього
рівняння цієї підсистеми має вигляд
![]() .
.
Підставимо
його в передостаннє рівняння. Одержуємо
![]() .
Загальний розв’язок лінійного
неоднорідного рівняння має вигляд суми
загального розв’язку однорідного і
частинного розв’язку неоднорідних
рівнянь, тобто
.
Загальний розв’язок лінійного
неоднорідного рівняння має вигляд суми
загального розв’язку однорідного і
частинного розв’язку неоднорідних
рівнянь, тобто
![]() .
Загальний розв’язок однорідного має
вигляд
.
Загальний розв’язок однорідного має
вигляд
![]() .
.
Частинний
розв’язок неоднорідного шукаємо методом
невизначених коефіцієнтів у вигляді
![]() ,
,
де
![]() -
невідома стала. Підставивши в неоднорідне
рівняння, одержимо
-
невідома стала. Підставивши в неоднорідне
рівняння, одержимо ![]() .
.
Звідси
![]() і загальний розв’язок неоднорідного
рівняння має вигляд
і загальний розв’язок неоднорідного
рівняння має вигляд
![]() .
.
Піднявшись
ще на один крок нагору одержимо
![]() .
Продовжуючи процес далі, маємо
.
Продовжуючи процес далі, маємо
![]() .
Або у векторно - матричному вигляді
.
Або у векторно - матричному вигляді
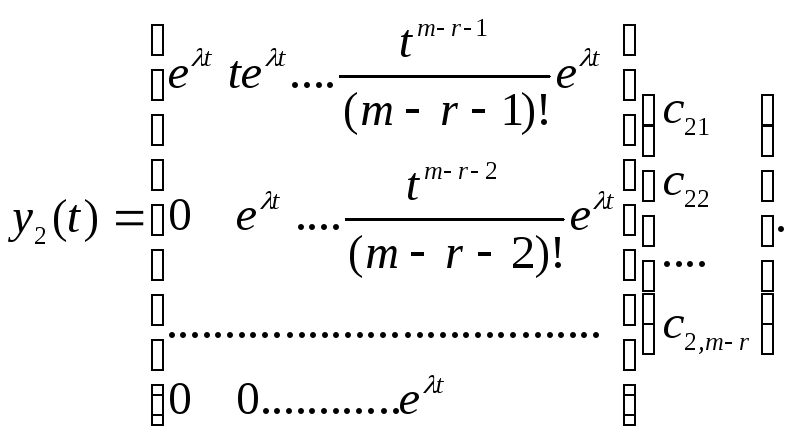 .
Додавши першу підсистему, одержимо
.
Додавши першу підсистему, одержимо
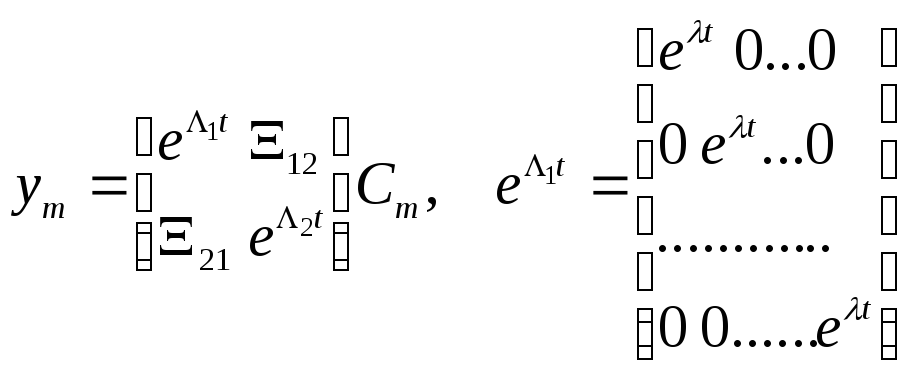 ,
,
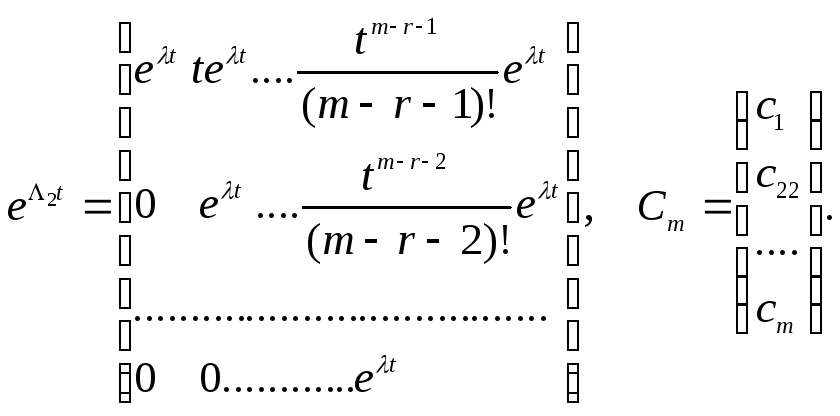
Для
останніх двох випадків матриця
![]() знаходиться як розв’язок матричного
рівняння
знаходиться як розв’язок матричного
рівняння ![]() .
.
