16. Сложение гармонических колебаний одного направления и частоты.

Пусть точка участ-ет в 2 колебания вдоль одного направления.

Найдем результирующие колебания :

х₁=А₁ х₂=А₂ х=х₁+х₂=А

Результирующие колебание будет с такой же частотой ω, амплитудой А и начальной фазой . Для нахождения амплитуды и начальной фазы будем использовать метод векторных диаграмм, т.е.гармонические колебания х₁ и х₂ будем представлять как векторы А₁ и А₂ вращающиеся с угловой скоростью ω .Покажем, что а задается выражением: А²=А²₁+А²₂+2А₁А₂

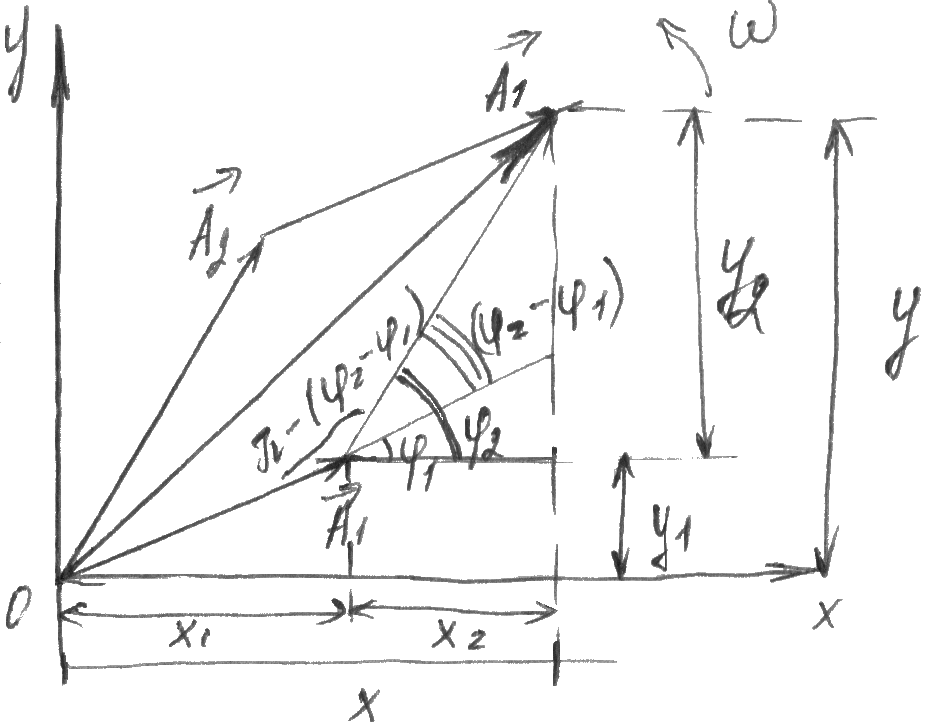
(рисунок - по теореме косинусов)

Начальная фаза

х=А

Рассмотрим частные случаи: 1) =2πn, n=0,±1,±2…, А=А₁+А₂

Два колебания одинаковой частоты одинаково или противоположно направленные наз. Когерентными.

2)=(2n+1)π, n=0,±1,±2., А=А₁-А₂

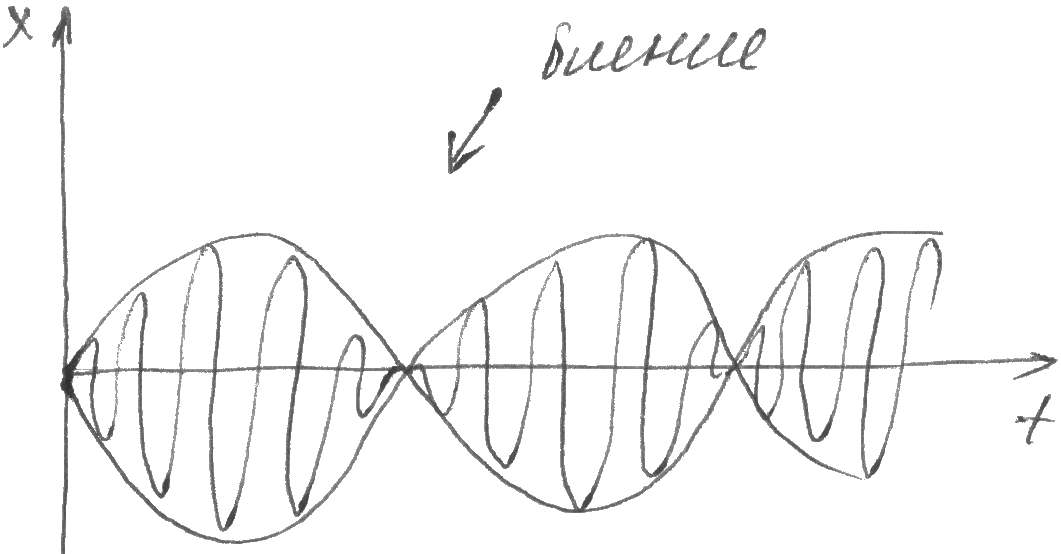
Если частоты складывают одного направления разные, то результирующее колебание будет не гармоническим. Если частоты складываемых одного направления близки друг к другу, то возникает колебания с периодически меняющейся амплитудой - биения. Пусть 2 одинаково направленных колебания имеют одинаковую амплитуду, близкие частоты, нулевые начальные фазы. х₁=А₁ х₂=А₂ () х=х₁+х₂=2А ; 2А=А_б

17. Сложение взаимно перпендикулярных гармонических колебаний.

Найдем результат сложения 2 гармонических колебаний с одинаковой частотой ω, происходящих во взаимно перпендикулярных направлениях. Пусть начальная фаза колебаний по х=0.а по у отлична от нуля : х =А у=В; ; ; ; (*).

Уравнение *есть уравнение эллипса произвольно ориентированного относительно координатных осей ХУ, т.е. траектория результирующих колебаний есть эллипс. Такое наз. эллиптически поляризованным.Если складывать 2 колебания с одинаковыми частотами, но разными начальными фазами. : х=А у=В, тогда .Рассмотрим частные случаи:

1) ; =0; ;

;

2); ;

3); -эллипс.

Если А=В, то получаем уравнение окружности(). Если частоты взаимно перпендикулярных колебаний различны, то получается сложная фигура Лиссажу: ω₁/ω₂ = n/m.

18. Затухающие колебания.

Свободные колебания - колебания происходящие под действием внутренних квазиупругих сил. Затухающие - колебания на которые действуют квазиупругие силы, силы трения, тяжести при этом энергия системы убывает, амплитуда - убывает. Рассмотрим затухающие колебания в одномерном случае . При малых колебания сила пропорциональна скорости ; знак «-» означает,что сила трения направлена против оси. По 2 з. Ньютона: ; ; - диф. уравнение затухающих колебаний. Для решения данного ур-ия введем новую переменную ; .Найдем частные производные: ; . Пусть , то есть трение очень мало, тогда: ; ; ; ; .

А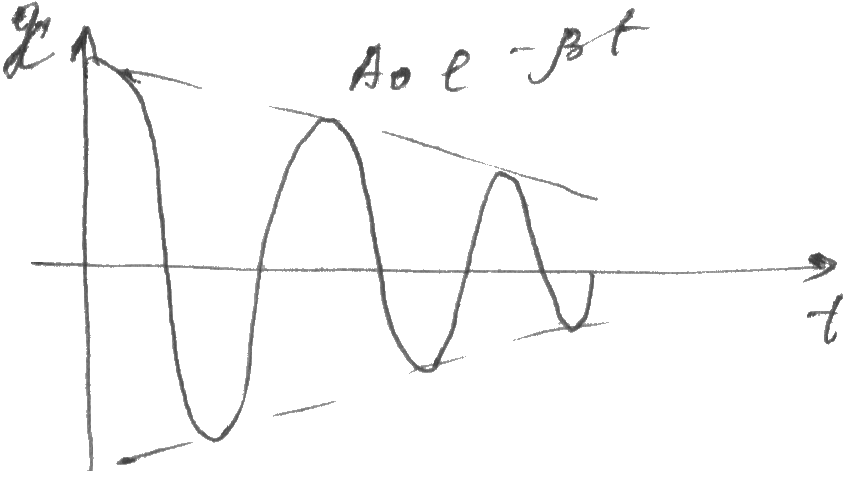мплитуда затухающих колебаний -амплитуда убывает по exp со временем.

β - характеризует степень затухания колебаний. –период затухающих колебаний. Если трение сопротивления в системе велико ,то результирующее движение апериодическое. Декремент затухания - отношений 2 последовательных амплитуд отличающихся на период. . Логарифмическим декрементом наз. Натуральный логарифм от декремента затухания , , . Пусть время τ, время за которое амплитуда колебаний уменьшается в раз и система совершает полных , , =1, . Логарифмический декремент затухания обратен числу полных колебаний после совершения которых амплитуда уменьшается в раз. Добротности колеблющегося контура Q при малых колебаниях обратно пропорционален логарифмическому декременту. ,