6О. Момент инерции тела. Теорема Штейнера.

I_zi=m_i*z_i²

I_z=m_i*z_i²

Момент инерции тела отн-но некот-ой оси есть сумма моментов инерции отдельных частиц , сост-щих это тело. В пределе, когда число разбиений :

I_z=²dm

где суммирование ведётся по всей массе тела.

dm=dV

I_z=²dxdydz

r²=x²+y²+z²

Сопоставим ур-ие дв-ния поступ-го и вращ-го дв-ния.

F_s=m_s*a_s

M_z=I_z*

Момент инерции тела во вращ-ом дв-нии аналогичен массе в пост-ом дв-нии. Т.е. момент инерции тела есть мера инертности тела во вращ-ом дв-нии.

Масса-мера инертности тела в пост-ом дв-нии. Инертность – cв-во тела сохр-ть сост-ие покоя или равно-го прямолин-го дв-ния в отсутствии действия сил. Во вращ-ом дв-нии если тело имеет большой момент инерции, то тело стрем-ся сохр-ть сост-ие покоя или равном-го вращения.

Рассмотрим моменты инерции тел в простейших случаях.

1.момент инерции точки массы m на раст-нии r от оси есть величина

I_z=mr² [I_z]=кг*м²

2. момент ин-ции однородного кольца или полого цилиндра

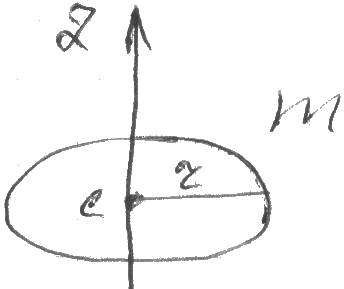
I_z=mr²

3. диск или сплошной цилиндр

I_z=mr²

4. момент инерции шара

I_z=mr²

5. момент инерции стержня

I_z=ml²

6. момент инерции стержня отн-но оси, прох-щей через его конец

I_z=ml²

Момент инерции тела не зависит от вращения тела. Зависит от формы тела, его размеров, распределения плотности массы в теле и от выбора оси.

Центром инерции тела (центром масс, центром тяжести) наз-тся т. с радиус-вектором

где суммир-ние ведётся по всем частицам тела.

r_i-радиус вектора i-ой частицы

В проекции на координатные оси имеем

Т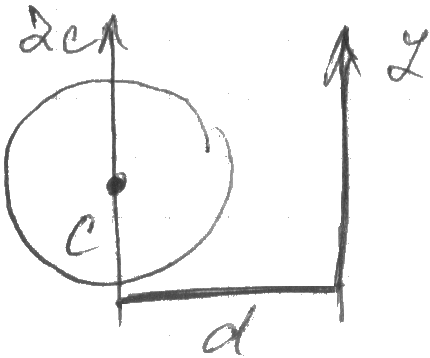-ма Штейнера: момент инерции тела отн-но оси z равен моменту ин-ции тела отн-но-ой оси z_c , прох-щей через центр инерции тела, сложенному с произв-ем массы тела m на квадрат расст-ия d между осями.

I_z=I_zc+md²

Д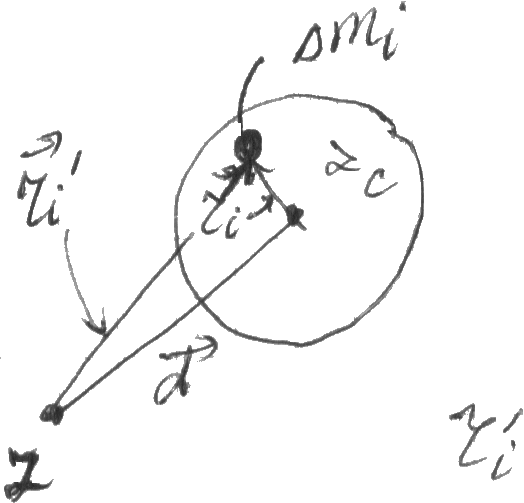ок-во: пусть ось z неподвижна так, что траект-ии всех частиц тела лежат в пл-стях. Ось z проходит через центр тела. Расст-ие между осями d.

Из рисунка =+

Возведём 2 этих части в квадрат

=+d²+2

Домножим обе части на и просуммируем по всем элементам тела

(по определению радиус-вектора центра инерции)

I_z=I_zc+md²

Ч.Т.Д.

Между кинематикойи динамикой пост-го и вращ-го дв-ния сущ-ют сходства:

Поступ.	Вращ.
, x
а	β
m	Iz
P=m	Lz=
F	Mz (момент силы)
F=ma	Mz=Iz

7О. Закон сохранения импульса.

Рассмотрим систему мат-ых т. , сост-щую из n точек. Силы, действующие между т-ми системы наз-ся внутренними. Прочие – внешними.

Система наз-тся замкнутой (изолированной) если отсутствуют внешние силы.

Пусть на i-ую точку системы действуют внешние силы с равнодействующей и внутренней силой .

По 2-му з.Ньютона имеем ур-ие дв-ния для m мат-ых точек.

= m_i

ki означает, что нет самодействия

==….=0

Проссумируем ур-ие 1 по всем точкам системы.

Слагаемое = 0, т.к. по 3 з. Ньютона =

Поэтому в сумме (3) =; = и т. д. поэтому она =о

Импульсом системы тел (точек) наз-тся векторная сумма импульсов отдельных точек системы.

Закон изменения импульсов системы

Производная по времени от вектора импульса системы точек (тел) равна вект-ой сумме всех внешних сил, приложенных к системе.

Если внешних сил нет (=0), то =0, тогда =соnst.

Закон сохранения импульса системы : импульс замкнутой системы мат-ых точек (тел) сохраняется.

m₁₁+ m₂₂+….= m₁₁+ m₁₁+….

ЗСИ применим также в теории относительности

ЗСИ связан с однородностью пространства, т.е. симметрии законам физики по отношению к пространственным сдвигам начала координат (по отн-ию к трансляциям).

В однородном пр-стве перенос замкнутой системы как целого не меняет законов дв-ния системы. Пустое пр-ство однородно.

Покажем теперь, что поступ-ое дв-ние тела можно заменить дв-ем центра масс тела, т.е. дв-ем одной точки. Пусть тело массой М поступ-но движется со скоростью . Радиус-вектор центра масс тела

m_i – масса i-ой частицы тела

r_i – радиус-вектор i-ой частицы

Продифф-ем r_c по t

Возьмем производную