29. Средства преобразования Лоренца.

А) относительность одновременности

Каждое событие (вспышка света) хар-ся 3-мя координатами x, y, z и временем t. Каждому событию соответствует 4-мерную точку.

Для сравнения момента времени ,когда происходит 2 события в разных точках. Нужно поместить в эти точки часы и убедиться, что часы идут синхронно. Для синхронизации часов применяется следующая процедура: Из точки А отправляется световой сигнал в т. В. В т. В свет-ой сигнал отражается и возвращается в т. А в момент времени t. Тогда говорят, что часы т.В синхронизированы с часами в т. А, если в момент возвращения светового сигнала в А из В часы показывают:

t =

События в т. А и в т. В одновременны, если соответствующие им отсчёты времени по часам А и В совпадают. Относительность одновременности обознач-т, что пространственно-разделённые одновременны в одной системе отсчёта оказ-ся разновременными в другой.

Пусть в системе S в момент времени t произошли события (напр. Вспышка света), , тогда в ситеме , тогда в ситеме эти события , в силу преобр-ий Лоренца *, произойдут в момент времени:

S’:

События одновременны в одномерной системе отсчёта оказываются не одновременными в другой СО.

Б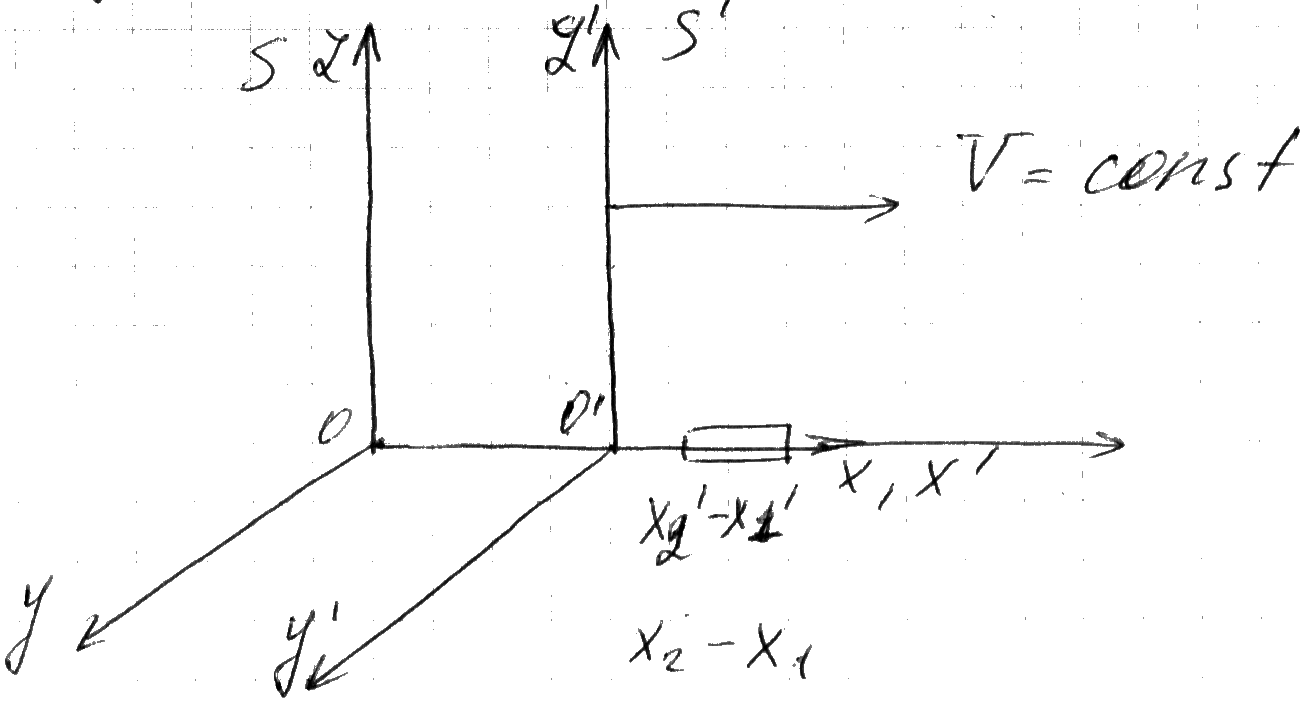) Сокращение продольных размеров движущегося тела. Стержень расположен вдоль оси S’ и покоится вдоль оси S., тогда длина стержня в системе S’ равна:

(0 - означает, что длина стержня измеряется в сопутствующей ситеме отсчёта, относительно кот. стержень покоится).

= l =

l - длина стержня, движущегося отн-но S, -покоящегося стержня (движущиеся тела сокращают свои размеры в продольном направлении, т. е. в напр-ии движ-я.

В) замедление хода движущихся часов.

Пусть в системе S’в т. происходит событие с длительностью ∆=

Длительность этого события в ситеме S , относительно кот. часы движутся со скоростью будет равна:

∆=

В силу преобр. Лоренца **,имеем:

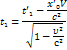
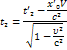
∆t =

означает, что длительность события измеряется по покоящимся часам, т. е. в S’.

∆t- длительность события в S.

Очевидно, что ∆t › =› движущиеся часы идут медленнее, чем покоящиеся, т. е. в движущейся системе отсчёта замедляется ход течения времени =›приходим к парадоксу часов (близнецов).

30. Релятивистский закон сложения скоростей.

Рассм. движение т.М в системах S и S^’ (υ = const): Пусть в сист.S будет момент врем. t, корд. т.М: , а скорости:

U_x= , U_y= , U_Z=

Пусть в сист.S^’ будет момент врем. t ’, корд. т.М: , а скорости:

= , = , =

Найдём связь скоростей т.М в S и S^’

В силу преобразований Лоренца имеем

=

Возьмём полный дифференциал от обеих частей последних равенств:

=

Из последнего в первых трёх формулах поделим соответственно левую и праву части на 4-ю формулу (получим систему):

; ;

Поделим числитель и знаменатель:

; ;

С учётом обозначений скоростей т.М в S и получаем закон преобразования релятивистских скоростей:

; ; (*)

, то получаем: U_X = U_X’ + V - теорема о сложении скоростей в классической механике.

Из (*) → ск-ти, большие релятив.скоростей, не могут получаться.

Фотон движ.со скор.