8. Несобственные интегралы 1-го и 2-го рода, их свойства. Признаки сходимости. Примеры. Абсолютная и условная сходимость несобственных интегралов. Примеры.

Пусть f(x) непрерывна на . Если существует конечный предел, то его называют несобственным интегралом первого рода и обозначают . В этом случае говорят, что несобственный интеграл сходится. Если же указанный предел не существует ил он бесконечен, то говорят, что интеграл расходится.

Несобственный интеграл с двумя бесконечными пределами определяется формулой .

Несоб. Инт. Выражает площадь бесконечно длинной криволинейной трапеции.

Пусть функция f(x) непрерывна на промежутке [a;b) и имеет бесконечный разрыв при x=b. Если существует конечный предел , то его называют несобственным интегралом второго рода.

Если предел в правой части существует, то несобственный интеграл сходится. Если не существует или бесконечен, то расходится.

Признаки сходимости.

Признак сравнения

Если на промежутке непрерывные функции f(x) и удв. условию , то из сходимости интеграла следует сходимость интеграла , а из расходимости интеграла следует расходимость .

Теорема

Если существует предел , то интегралы и одновременно оба сходятся или оба расходятся (ведут себя одинаково в смысле сходимости)

[II род]

Если на промежутке непрерывные функции f(x) и непрерывны, при x=b терпят бесконечный разрыв и удв. условию , то из сходимости интеграла следует сходимость интеграла , а из расходимости интеграла следует расходимость .

Теорема

Пусть функции f(x) и непрерывны на [a;b) и в точке x=b терпят разрыв. Если существует предел , то интегралы и одновременно оба сходятся или оба расходятся (ведут себя одинаково в смысле сходимости)

9. Вычисление площадей плоских фигур в декартовых и полярных координатах (вывод)

Декартовы координаты.

Пусть криволинейная трапеция ограничена линиями y=f(x) > 0 , x=a, x=b, y=0; Для нахождения площади S:

1. Возьмем произвольное и будем считать, что S=S(x)

2. Дадим аргументу х приращение . Функция S=S(x) получит приращение 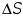, представляющее собой площадь элементарной криволинейной трапеции. Дифференциал площади dS есть главная часть приращения при , и, очевидно, он равен площади прямоугольника с основанием dx и высотой y: dS=ydx.

3. Интегрируя полученное равенство в пределах от x=a до x=b получаем

Если криволинейная трапеция расположена ниже оси Ох, то ее площадь может быть найдена по формуле

Площадь фигуры, ограниченной кривыми y=f₁(x) и y=f₂(x), прямыми x=a,. x=b (f₂(x) > f₁(x)) можно найти по формуле

Если криволинейная трапеция ограничена прямыми y=c и y=d, осью Оу и непрерывной кривой , то ее площадь:

Если криволинейная трапеция ограничена кривой, заданной параметрически,

прямыми x=a и x=b и осью Ох, то ее площадь

Полярные координаты

Найдем площадь S криволинейного сектора, т.е. плоской фигуры, ограниченной непрерывной линией и двумя лучами .

1) Будем считать часть искомой площади S как функцию угла

2) Если текущий полярный угол получит приращение , то приращение площади равно площади элементарного криволинейного сектора.

Дифференциал dS представляет собой главную часть приращения при м равен площади кругового сектора радиуса r с центральным углом .

3)Интегрируя полученное равенство в пределах от получим площадь: