5. Доказать теоремы об оценки и о среднем для определенного интеграла.

Теорема о среднем. Если функция непрерывна на отрезке [a;b], то существует точка такая, что

<Д>

По формуле Ньютона-Лейбница имеем

Где F’(x) = f(x). Применяя к разности F(b)-F(a) теорему Лагранжа (теорему о конечном приращении функции), получим

</Д>

Геометрический смысл: при f(x) > 0 значение определенного интеграла равно, при некотором площади прямоугольника высотой f(c) и основанием (b-a). Число

называется средним значением функции f(x) на [a;b].

Оценка интеграла.

Если m и M –соответственно наименьшее и наибольшее значения функции y=f(x) на отрезке [a;b], (a<b), то

<Д>

Так как для любого имеем m < f(x) < M то по свойству имеем:

Применяя к крайним интегралам теорему о среднем получаем

</Д>

6. Определенный интеграл с переменным верхним пределом. Доказать теорему о производной интеграла с переменным верхним пределом. Вывести формулу Ньютона-Лейбница.

Пусть f(x) интегрируема на [a;b]. Тогда для функция f(x) интегрируема на [a;x]. Поэтому на интервале (a;b) определена , которую называют определенным интегралом с переменным верхним пределом.

Производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции, в которой переменная интегрирования заменена этим пределом, т.е.

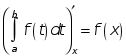
<Д>

По формуле Ньютона-Лейбница имеем:

Следовательно,

</Д>

Это означает, что определенный интеграл с переменным верхним пределом есть одна из первообразных подынтегральной функции.

Формула Ньютона-Лейбница.

Если y=f(x) непрерывна на [a;b] и F(x) – какая-либо ее первообразная на [a;b] (F’(x)=f(x)), то имеет место формула

<Д>

С помощью точек x₀=a, x₁,x₂,…,x_n=b (x₀<x₁<…<x_n) разобьем отрезок [a;b] на n частичных отрезков [x₀;x₁],[x₁,x₂],…[x_n-1,x_n]

Рассмотрим тождество

Преобразуем каждую разность в скобках по формуле Лагранжа.

Получим

Где c_i – некоторая точка интервала [x_i-1;x_i]. Так как y=f(x) непрерывна на [a;b], то она интегрируема на этом интервале. Поэтому существует предел, равный определенному интегралу f(x) на [a;b]. Переходя к пределу, получаем:

</Д>

7. Вычисление определенного интеграла подстановкой и по частям (вывод). Интегрирование четных и нечетных функций на отрезке, симметричном относительно начала координат (вывод), интегрирование периодических функций. Примеры.

Интегрирование подстановкой.

Теорема.

Если

1. ф-я и ее производная непрерывны при

2. множеством значений функций при 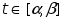является отрезок [a;b]

3. 

то

<Д>

Пусть F(x) есть первообразная для f(x) на [a;b]. Тогда по формуле Ньютона-Лейбница . Т.к. , то является первообразной для ф-и. Поэтому по формуле Ньютона-Лейбница:

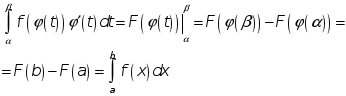
</Д>

При вычислении определенного интеграла методом подстановки возвращаться к старой переменной не требуется..

Не следует забывать менять пределы интегрирования при замене переменных!

Интегрирование по частям

Теорема.

Если функции u = u(x) и v=v(x) имеют непрерывные производные на [a;b], то

<Д>

На [a;b] имеет место равенство (uv)’=u’v+uv’. Следовательно, функция uv есть первообразная для непрерывной функции u’v+uv’. Тогда по формуле Ньютона-Лейбница имеем

</Д>

Интегрирование четных и нечетных функций в симметричных пределах

Пусть функция f(x) непрерывна на [-a;a], симметричная относительно начала координат. Тогда

, если f(x) - четная

, если f(x) – нечетная

<Д>

разобьем отрезок на части [-a;0] и [0;a]. Тогда по свойству аддитивности:

В первом интеграле сделаем подстановку x=-t (согласно свойству : «определенный интеграл не зависит от обозначения переменной интегрирования»)

Подставляя обратно получаем

Если f(x) четная, f(-x)=f(x), то f(-x)+f(x)=2f(x)

Иначе f(-x)=-f(x), то f(-x)+f(x)=0

</Д>