
- •Электроматериаловедение
- •Предисловие
- •I. Содержание дисциплины Рабочая программа
- •Раздел 1. Диэлектрики (24 часа)
- •Раздел 2. Полупроводники (12 часов)
- •Раздел 3. Проводники (18 часов)
- •Раздел 4. Магнитные материалы (20 часов)
- •Тематический план лекций
- •Примерный перечень лабораторных работ (12 часов)
- •II. Задание на контрольную работу
- •Задача 1
- •Задача 2
- •Задача 3
- •Задача 4
- •Вопросы для самопроверки
- •III. Методические указания к выполнению контрольной работы задача 1
- •Задача 2
- •Задача 3
- •Задача 4
Задача 2
Электрическое поле кабеля подобно полю цилиндрического конденсатора, которое характеризуется осевой симметрией.
Последовательность решения следующая.
1. В соответствии с теоремой Гаусса, напряженность электрического поля по толщине изоляции выражается формулой
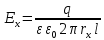
где
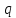 – заряд жилы кабеля, Кл;
– заряд жилы кабеля, Кл;
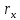 – переменная величина, определяющая
гиперболический закон
– переменная величина, определяющая
гиперболический закон
изменения напряженности электрического поля по толщине изоляции кабеля, м;
l – длина кабеля, м;
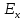 – напряженность электрического поля,
кВ/м.
– напряженность электрического поля,
кВ/м.
2. Напряжение между жилой кабеля и свинцовой оболочкой выражается через определенный интеграл вектора напряженности поля по пути убывания (знак минус) потенциала вдоль направления силовых линий:
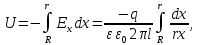
откуда
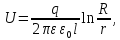
где
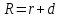 – внутренний радиус свинцовой оболочки,
мм;
– внутренний радиус свинцовой оболочки,
мм;
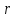 – радиус
медной жилы, мм;
– радиус
медной жилы, мм;
 – толщина
изоляции, мм;
– толщина
изоляции, мм;
 -
напряжение, кВ.
-
напряжение, кВ.
3. В соответствии с определением ёмкости кабеля, как отношения заряда к напряжению, имеем
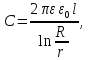
где
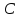 – ёмкость кабеля, Ф.
– ёмкость кабеля, Ф.
4.
Подставив в (1)
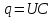 ,
получим
,
получим
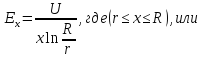
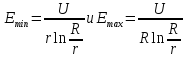
5. Реактивная мощность в кабеле (зарядная мощность) определяется из
выражения
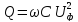
где
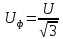 -
фазовое напряжение, В;
-
фазовое напряжение, В;
ω=2πf – круговая частота поля, Гц.
Задача 3
Согласно ПУЭ проводники любого назначения должны удовлетворять требованиям в отношении предельно допустимого нагрева. Количество теплоты, выделяемое ежесекундно в проводе сопротивлением R в проходящем токе I определяется выражением
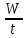 =
I2R
,
=
I2R
,
где W – количество теплоты, Вт; t – время, с.
Часть этого тепла идет на повышение температуры провода, а другая часть рассеивается в окружающей среде.
В установившемся тепловом режиме количество рассеиваемого ежесекундно тепла станет равным количеству тепла, выделяемого током. Уравнение теплового баланса имеет следующий вид
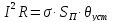 ,
,
где
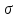 – коэффициент теплоотдачи, Вт/мм 2 ·
град;
– коэффициент теплоотдачи, Вт/мм 2 ·
град;
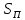 – поверхность охлаждения провода, мм
2 ;
– поверхность охлаждения провода, мм
2 ;
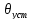 – установившаяся разность температур
провода и окружающей
– установившаяся разность температур
провода и окружающей
среды:
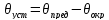 .
.
Плотность тока определяется из выражения
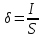 ,
,
где δ – плотность тока, А/мм2 .
Сопротивление провода
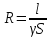 ,
,
где l – длина провода, м;
S=
 - сечение провода (диаметр
- сечение провода (диаметр
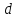 ),
),
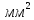 ;
;
γ – удельная проводимость токоведущей жилы провода
(обратная
величине удельного сопротивления),
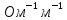 ;
;
R – сопротивление провода, Ом.
Принимаем в первом приближении, что поверхность охлаждения равна
боковой поверхности цилиндрического провода, т.е.
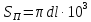 ,
где
,
где
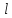 выражено в мм.
выражено в мм.
Уравнение теплового баланса будет иметь вид
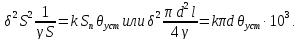
Соответственно получим, что плотность тока определяется из выражения:
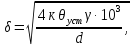
где δ – плотность тока, А/мм2.
Допустимая
плотность тока
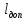 получается, если в это выражение
подставить значение γ=γθ,
т.е. удельную проводимость проводника
при изменении температуры до θпред.
При нагреве сопротивление проводника
возрастает. Температурный коэффициент
сопротивления
получается, если в это выражение
подставить значение γ=γθ,
т.е. удельную проводимость проводника
при изменении температуры до θпред.
При нагреве сопротивление проводника
возрастает. Температурный коэффициент
сопротивления
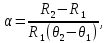
где
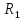 – сопротивление проводника при
температуре
– сопротивление проводника при
температуре
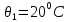 ,
т.е. температуре, для которой приводятся
в справочниках удельные сопротивления
(проводимости) материалов;
,
т.е. температуре, для которой приводятся
в справочниках удельные сопротивления
(проводимости) материалов;
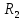 – сопротивление
проводника, соответствующее температуре:
– сопротивление
проводника, соответствующее температуре:
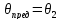 ;
;
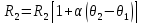 .
.
При
нагреве провода до
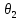 его удельное сопротивление возрастает
до
его удельное сопротивление возрастает
до
значения
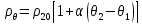 ,
,
и, следовательно,
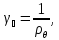
Параметры
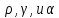 задаются в справочниках для каждого
материала проводника. Получив для
предельной температуры
задаются в справочниках для каждого
материала проводника. Получив для
предельной температуры
 ,
определяем длительно допустимый ток:
,
определяем длительно допустимый ток:
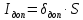 ,
,
где
S – площадь сечения провода,
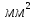 .
.
Рабочий ток определяется по формуле:
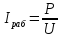
где
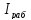 – рабочий ток, А.
– рабочий ток, А.
После полученных результатов необходимо сделать вывод о работе устновки.
