8. Игры с природой. Критерий Байеса

Неопределённость, сопровождающая операцию, может быть связана с недостаточной осведомлённостью оперирующей стороны об условиях, в кот-х выполняется операция. Внешняя среда, в условиях кот-й оперирующая сторона принимает решение и от кот-й зависит исход операции наз-ся природой.

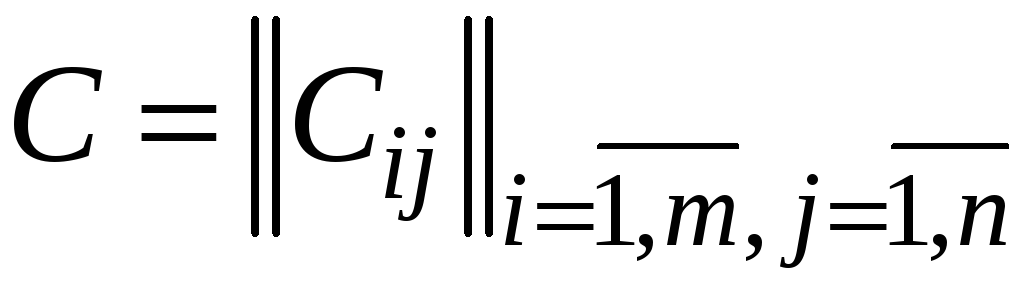Пусть у сознательного игрока А имеются m стратегий , а о состоянии природы можно сделать n предположений. Матрица выигрыша состоит из элементов , кот-е составляют выигрыш, кот-й получит игрок А, если выберет стратегию в то время, когда природа будет находится в состоянии

В платёжной матрице можно исключать доминируемые и дублируемые строки, убирать таким же образом столбцы нельзя, поскольку природа может реализовать любое своё состояние. Матрица платежей не даёт полной информации о преимуществе одних стратегий над другими. Например, если , то отсюда не следует, что стратегия лучше чем , возможно состояние природы более благоприятно, чем состояние природы . Такую дополнительную информацию игроку даёт матрица рисков. Число называют риском для игрока А при исполнении стратегии , когда природа находится в состоянии . Это число равно разности между тем выигрышем, который имел бы игрок зная состояние , и тем выигрышем, который имеет выбирая стратегию , т. е. .

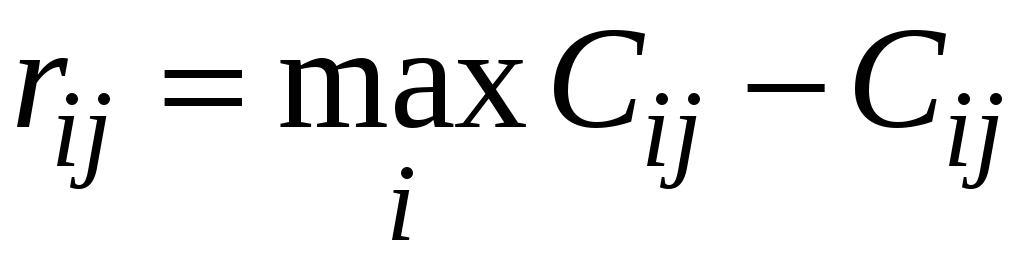Критерий Байеса

Предположим, что известны состояния природы 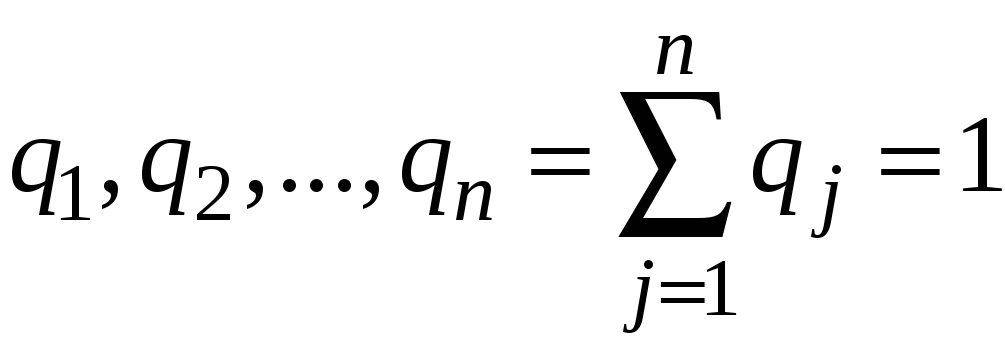. По критерию оптимальной является стратегия, для которой средний выигрыш максимален. 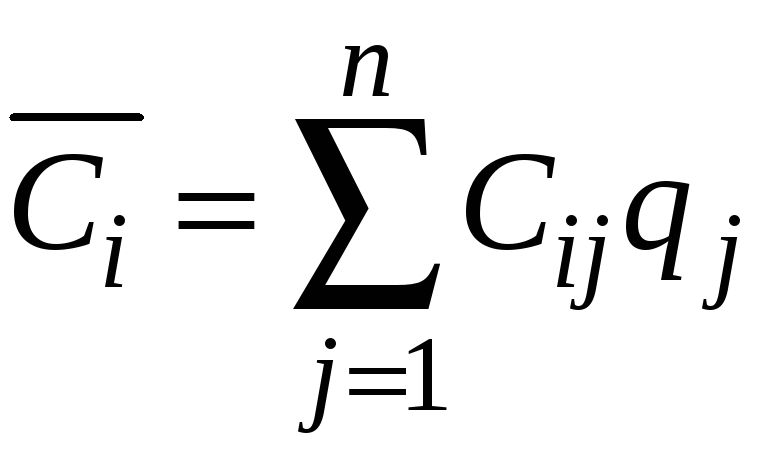–среднее значение выигрша.

Предположим, что для примера q= (0.1; 0.2; 0.5; 0.2)

Тогда =1*0.1+4*0.2+5*0.5+9*0.2=5.2

=3*0.1+8*0.2+4*0.5+3*0.2=4.5

=4*0.1+6*0.2+6*0.5+2*0.2=5

Максимальной является , значит, оптимальной по критерию Байеса является стратегия .

Легко показать, что стратегия максимизирующая средний выигрыш минимизирует средний риск

(, ).

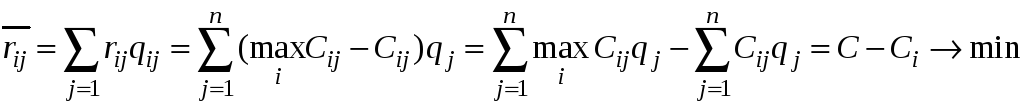Если известны вероятности состояния природы, то при решении игры всегда можно обойтись только чистыми стратегиями. Действительно, выберем произвольную смешанную стратегию ,,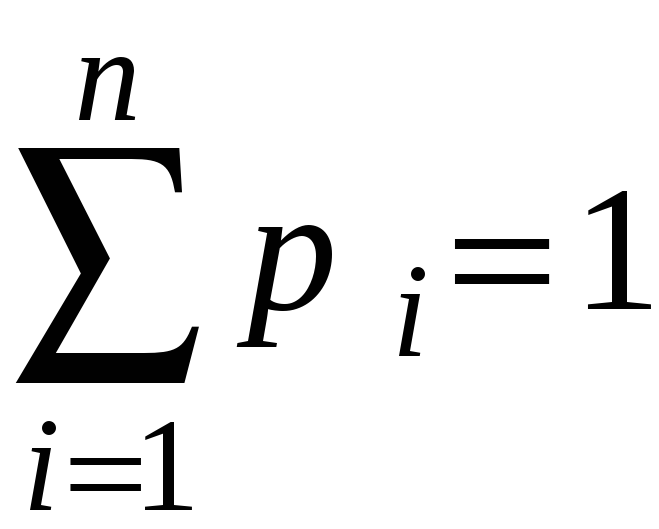 тогда средний выигрыш для неё

Пользуясь любой чистой оптимальной стратегией мы получим значение не меньше используя смешанную. Если известно, что все состояния природы равновероятностны, то полагают 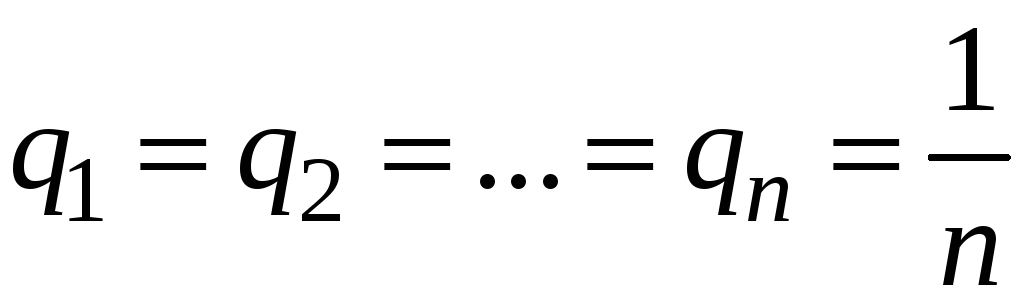и далее используют критерий Байеса. Такое предположение называется принципом недостаточного обоснования Лапласа.

Если удаётся оценить состояние природы по степени правдоподобности, то вероятности полагают пропорциональными членам убывающей арифметической прогрессии, т. е.

Так как 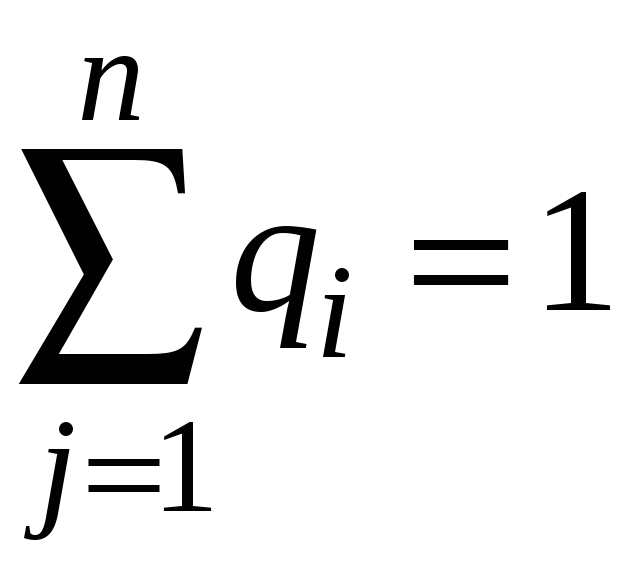, то ,

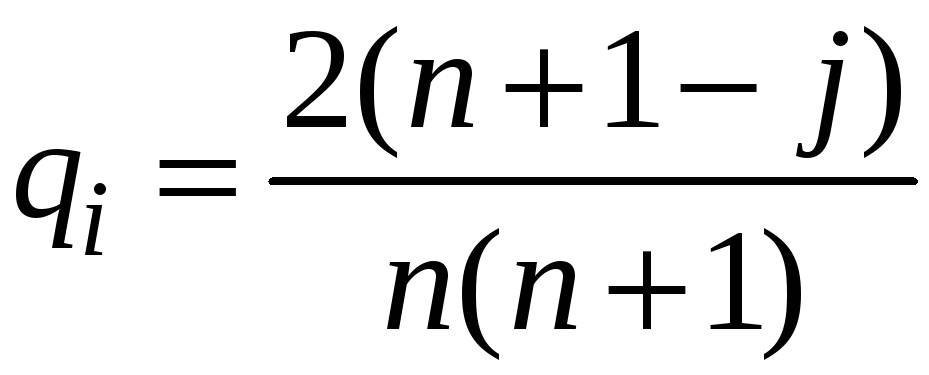Критерий Вальда.

По этому критерию оптимальной считается та стратегия, которая обеспечивает выигрыш не меньший, чем при наихудшем состоянии природы. Т.е. мы ищем стратегию, на которой достигается величина .

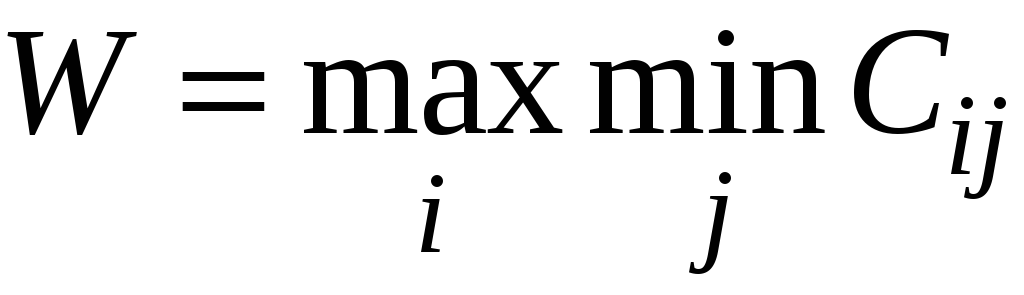Для примера 1

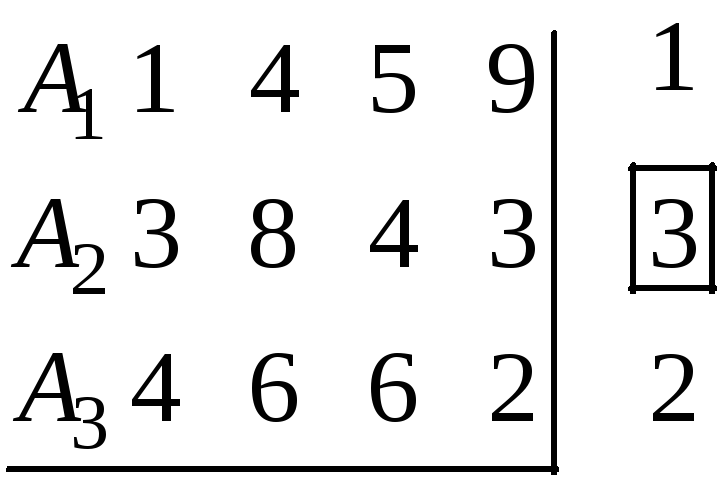
По критерию Вальда оптимальной является стратегия .

Пример 2.

. Матрица риска

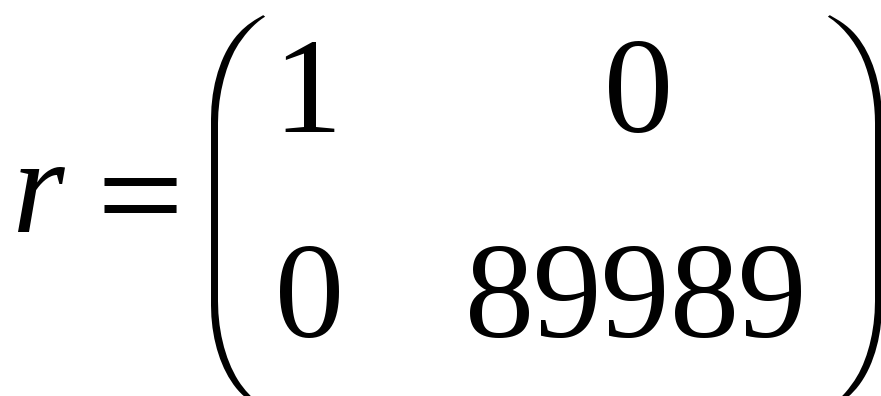
Оптимальной является стратегия .

Однако, интуитивно понятно, что выбирая можно надеется получить выигрыш 900000.

_{Критерий Сэвиджа. Критерий Гурвица.}

Критерий Сэвиджа. Оптимальной считается та стратегия, которая даёт наименьший риск в самых наихудших условиях..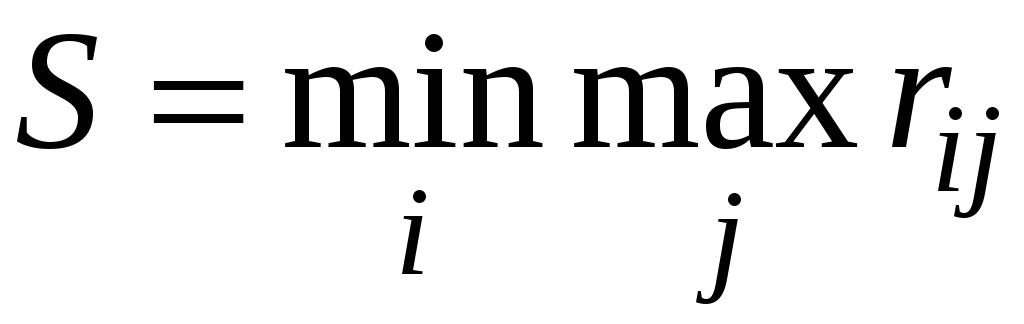

По критерию Сэвиджа для примера 1 оптимальной является стратегия .

Критерий Гурвица.

Согласно этому критерию следует ориентироваться не на крайний пессимистичный или оптимистичный, а выбирать стратегию, на которой выполняется

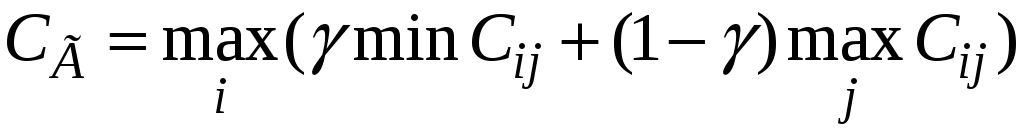,где — коэфф. пессимизма, .

Для примера 1.

При = 0,8

: .

: .

:

Оптимальной является стратегия