
- •1. Введение в исо. Предмет и история исо. Основные этапы и принципы операционного исследования. Постановка задач исо.
- •2. Постановка многокритериальной задачи.
- •3. Неопределенность природы и действий противника: принцип гарантированного результата
- •4. Основные понятия, принципы и классификация игр.
- •5. Решение матричных игр в смешанных стратегиях.
- •6. Решение игры 22
- •7. Упрощение игр
- •8. Игры с природой. Критерий Байеса
- •9. Бескоалиционные игры. Определение бескоалиционной игры. Равновесные ситуации и стратегии.
- •10. Теорема Нэша для бескоалиционных игр.
- •11. Методы анализа сетей. Потоки на сетях.
- •12. Теорема Форда-Фалкерсона
- •13. Комбинированные приложения з-чи о максимальном потоке. Простейшая з-ча о назначении.
- •I. Предварительный этап.
- •II. Этап расстановки пометок.
- •III. Этап переброски.
- •14. Классическая задача о назначении.
- •I этап. Приведение матрицы.
- •II этап. Выбор назначений.
- •III этап. Дополнительное приведение матрицы.
- •15. Основные этапы и понятия сетевого планирования и управления(спу)
- •17. Задача оптимального по времени распределения ограниченных ресурсов на сетевых графиках
- •19. Общая задача теории расписаний.
2. Постановка многокритериальной задачи.
Пусть
D
– некоторое множество, элементы которого
называются допустимыми решениями или
альтернативами, а функции
![]() заданные
на множестве D
– числовые функции, называемыми целевыми
функциями или критериями. Необходимо
найти оптимальное решение из множества
D
максимизирующее функции
заданные
на множестве D
– числовые функции, называемыми целевыми
функциями или критериями. Необходимо
найти оптимальное решение из множества
D
максимизирующее функции
![]() на
множестве D.
на
множестве D.
![]() (1)
(1)
f(x) – m-вектор-функция аргумента x.
Случаи,
когда функции
![]() достигают
максимума в одной и той же точке крайне
редки, поэтому основная проблема при
рассмотрении задачи (1) заключается в
формализации принципа оптимальности,
т.е. определение того, в каком смысле
оптимальное решение лучше других.
достигают
максимума в одной и той же точке крайне
редки, поэтому основная проблема при
рассмотрении задачи (1) заключается в
формализации принципа оптимальности,
т.е. определение того, в каком смысле
оптимальное решение лучше других.
Компромиссы по Парето
Опр.1.
Говорят,
что точка
![]() доминирует точку
доминирует точку
![]() ,
если
,
если
![]() ,
i=1,2,…,m
и
существует номер
,
i=1,2,…,m
и
существует номер
![]() ,
что
,
что
![]() .
.
Опр.2.
Точка
![]() называется
оптимальной по Паретто (эффективной),
если не существует
называется
оптимальной по Паретто (эффективной),
если не существует
![]() улучшающих
х.
улучшающих
х.
Учитывая
опр.1 и опр.2 мы заключаем, что множество
допустимых решений D
разбивается на два непересекающихся
множества
![]() - (D
–согласия) и
- (D
–согласия) и
![]() (D-
эффективная). Область согласия
(D-
эффективная). Область согласия
![]() не содержит недоминируемых точек (т.е.
любая точка множества
не содержит недоминируемых точек (т.е.
любая точка множества
![]() может быть улучшена). Эффективная область
(область компромисса)
может быть улучшена). Эффективная область
(область компромисса)
![]() содержит
все эффективные точки. В этой области
ни один из критериев не может быть
улучшен без ухудшения другого.
содержит
все эффективные точки. В этой области
ни один из критериев не может быть
улучшен без ухудшения другого.
Методы сведения многокритериальной задачи (МЗ) к однокритериальной: нормировка критериев, метод аддитивной свертки критериев.
Пусть
D
– некоторое множество, элементы которого
называются допустимыми решениями или
альтернативами, а функции
![]() заданные
на множестве D
– числовые функции, называемыми целевыми
функциями или критериями. Необходимо
найти оптимальное решение из множества
D
максимизирующее функции
заданные
на множестве D
– числовые функции, называемыми целевыми
функциями или критериями. Необходимо
найти оптимальное решение из множества
D
максимизирующее функции
![]() на
множестве D.
на
множестве D.
![]() (1)
(1)
f(x) – m-вектор-функция аргумента x.
При решении МЗ часто возникает проблема нормирования, т.е. приведения критериев к единому безразмерному виду:
1)замена
значений критериев относительными
величинами
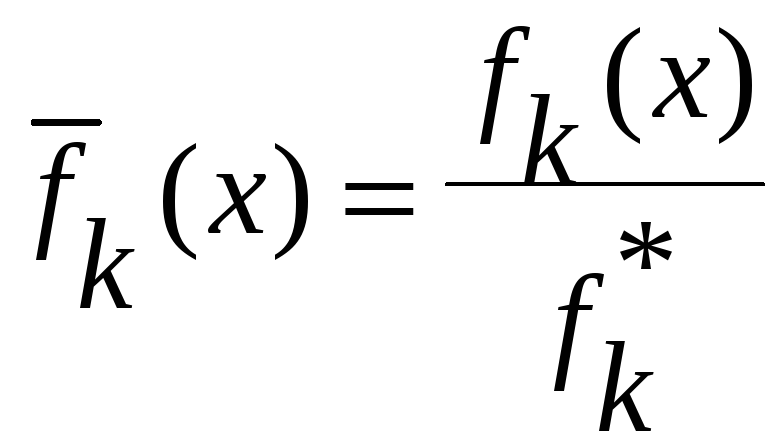 ,
где
,
где
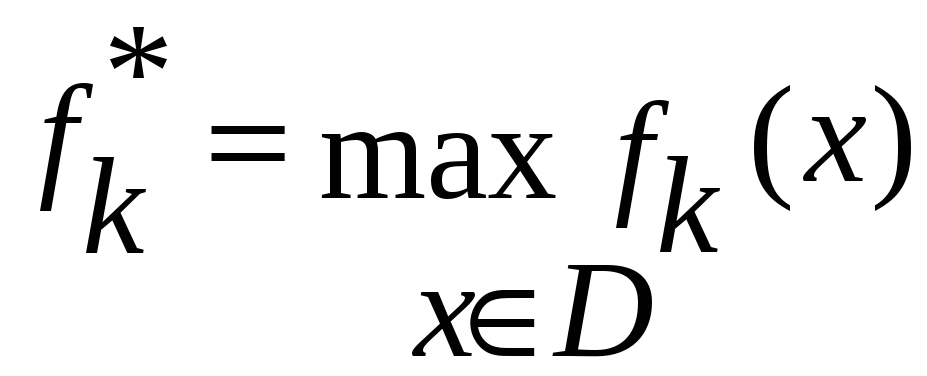 .
.
2)замена
значения критерия относительными
значениями отклонений от оптимальных
значений критериев, т.е.
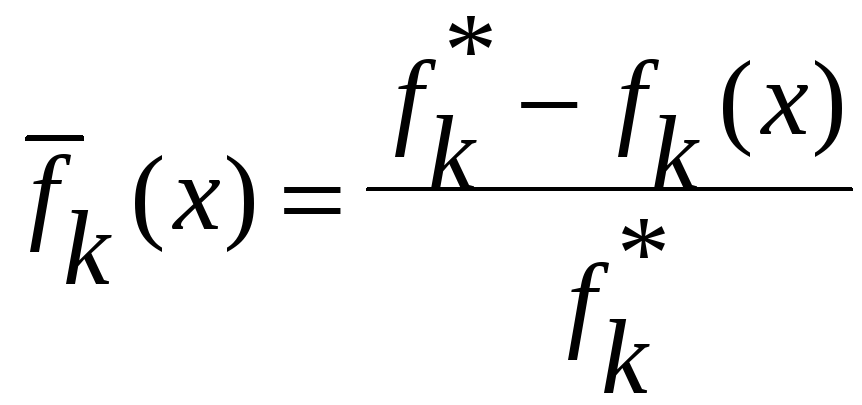 ,
,
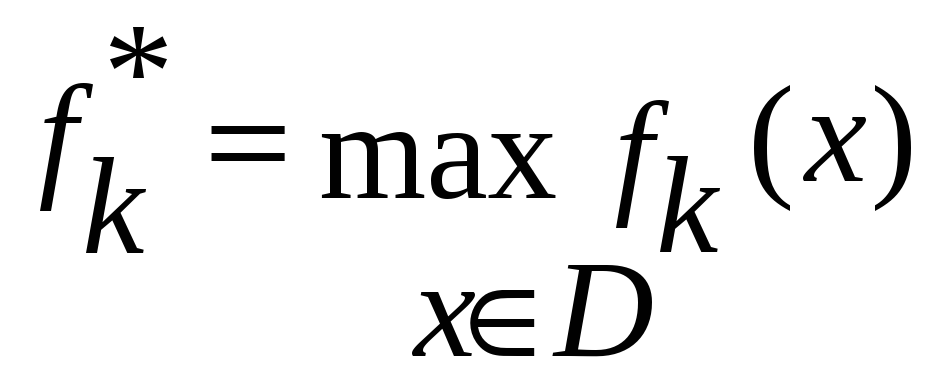 .
.
Метод аддитивной свертки критериев.
Пусть
критерии соизмеримы и определен вектор
весовых коэффициентов
![]() ,
характеризующих значимость соответствующего
критерия, причем
,
характеризующих значимость соответствующего
критерия, причем
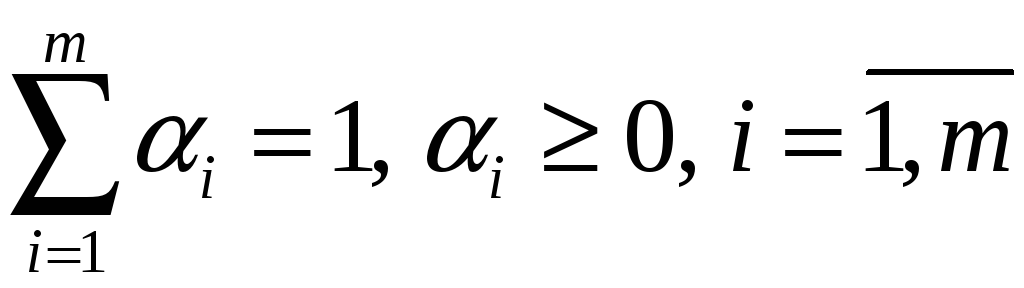 .
.
Т.о. решается задача оптимизации скалярного критерия
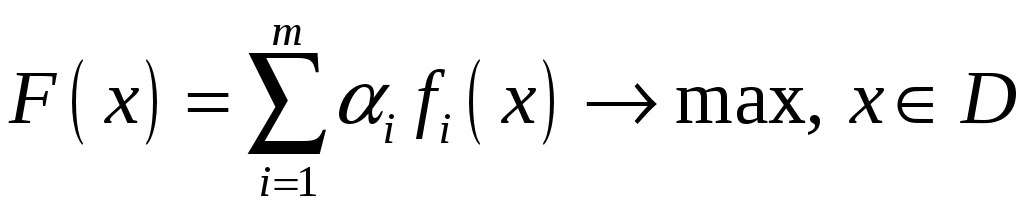 (2)
(2)
Решение задачи (2) эффективно для задачи (1).
Метод главного критерия.
Пусть
D
– некоторое множество, элементы которого
называются допустимыми решениями или
альтернативами, а функции
![]() заданные
на множестве D
– числовые функции, называемыми целевыми
функциями или критериями. Необходимо
найти оптимальное решение из множества
D
максимизирующее функции
заданные
на множестве D
– числовые функции, называемыми целевыми
функциями или критериями. Необходимо
найти оптимальное решение из множества
D
максимизирующее функции
![]() на
множестве D.
на
множестве D.
![]() (1)
(1)
f(x) – m-вектор-функция аргумента x.
Метод главного критерия заключается в следующем. Все функции, кроме 1-ой, главной, переводится в разряд ограничений.
Пусть
![]() - вектор, компоненты которого нижние
границы соответствующих критериев.
Оптимальным считается решение, при
котором критерий
- вектор, компоненты которого нижние
границы соответствующих критериев.
Оптимальным считается решение, при
котором критерий
![]() достигает своего максимального значения,
при условии, что по всем остальным
критериям достигнуты значения не меньше
заданных.
достигает своего максимального значения,
при условии, что по всем остальным
критериям достигнуты значения не меньше
заданных.
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
Метод ранжирования.
Критерии
нумеруются в порядке убывания их
важности. На первом шаге решается ЗО по
наиболее важному критерию.
![]() – область оптимальных решений по первому
критерию и т.д. На к-том
шаге решается задача
– область оптимальных решений по первому
критерию и т.д. На к-том
шаге решается задача
![]() ,
,
![]() ,
где
,
где
![]() - множество оптимальных решений
предыдущего шага. Основной недостаток
метода – уже на 1-ом шаге множество
оптимальных решений может содержать
только одну точку. И все остальные
критерии не участвуют в оптимизации.
- множество оптимальных решений
предыдущего шага. Основной недостаток
метода – уже на 1-ом шаге множество
оптимальных решений может содержать
только одну точку. И все остальные
критерии не участвуют в оптимизации.
Метод последовательных уступок. Метод целевого программирования
Пусть
D
– некоторое множество, элементы которого
называются допустимыми решениями или
альтернативами, а функции
![]() заданные
на множестве D
– числовые функции, называемыми целевыми
функциями или критериями. Необходимо
найти оптимальное решение из множества
D
максимизирующее функции
заданные
на множестве D
– числовые функции, называемыми целевыми
функциями или критериями. Необходимо
найти оптимальное решение из множества
D
максимизирующее функции
![]() на
множестве D.
на
множестве D.
![]() (1)
(1)
f(x) – m-вектор-функция аргумента x.
Метод последовательных уступок заключается в следующем.
1)критерии нумеруются в порядке убывания их важности;
2)определяются
значения
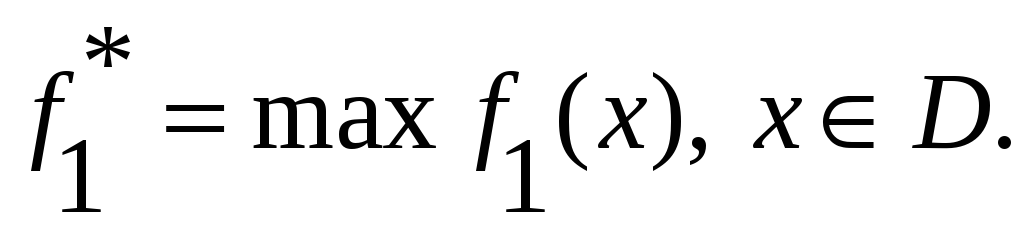

Лицом,
принимающим решение, устанавливается
величина уступки
![]() по этому критерию.
по этому критерию.
3)
решается задача
![]() ,
,
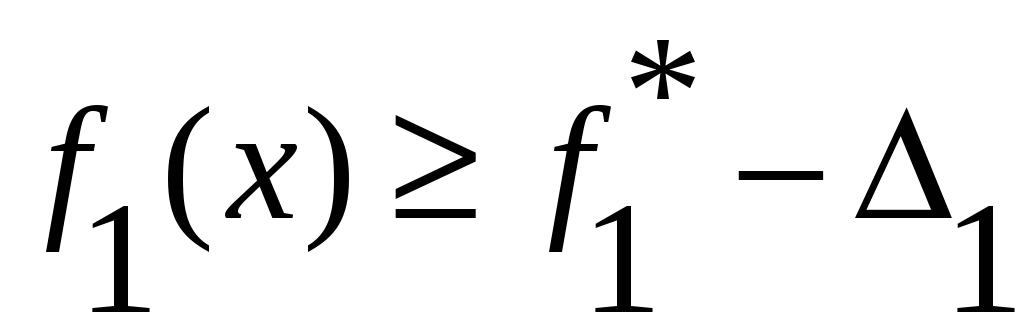 ,
,
![]()
Далее
2) и 3) повторяют для критериев
![]() .
Полученное решение не всегда является
эффективным.
.
Полученное решение не всегда является
эффективным.
Метод целевого программирования.
Пусть
решена система однокритериальных задач
![]() ,
,
![]() ,
,
![]() .
Получим решение
.
Получим решение
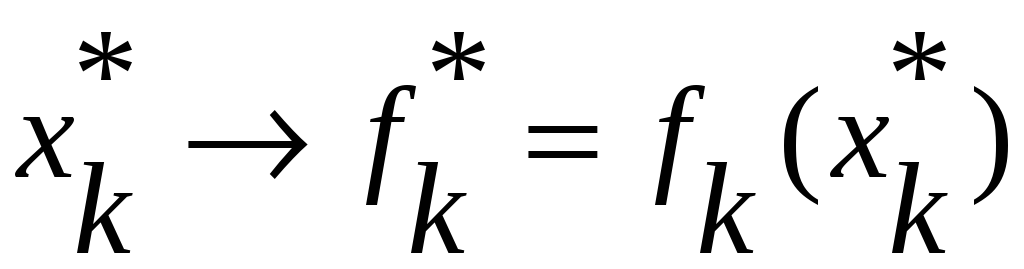 .
Определяем скалярную величину
.
Определяем скалярную величину
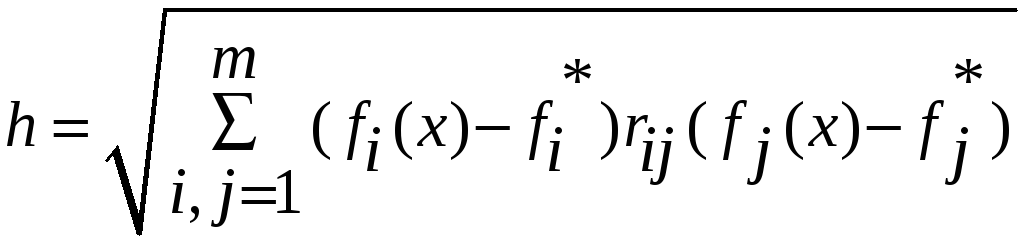 ,
где
,
где
![]() - элементы положительно определенной
матрицы
- элементы положительно определенной
матрицы
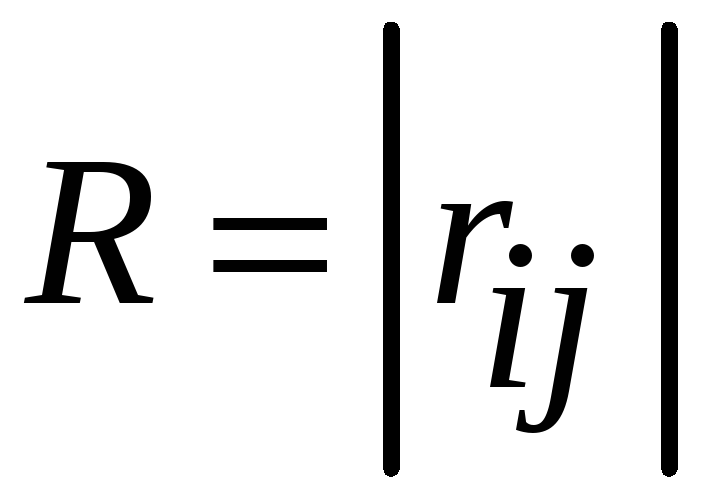 .
.
Если
![]() - единственная матрица, то
- единственная матрица, то
![]() определяет евклидово расстояние до
точки оптимума.
определяет евклидово расстояние до
точки оптимума.
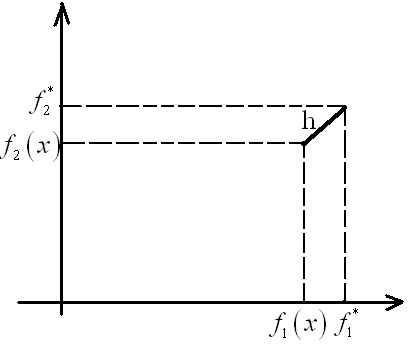
Решение
задач
![]() ,
,
![]() ,
позволяет найти точку
,
позволяет найти точку
![]() ,
которая ближе всего находится от точки
абсолютного оптимизма в метрическом
пространстве с расстоянием
,
которая ближе всего находится от точки
абсолютного оптимизма в метрическом
пространстве с расстоянием
![]() .
.
