Значение величин и при несовершенном сжатии

ω/ω1	0,10	0,20	0,30	0,40	0,50	0,60	0,70	0,80	0,90	1,00
δ	0,014	0,034	0,059	0,092	0,134	0,189	0,26	0,351	0,471	0,631
Δ1	0,019	0,042	0,071	0,107	0,152	0,208	0,278	0,365	0,473	0,608

При неполном сжатии коэффициент расхода вычисляют по уравнениям:

для круглых отверстий

μ₁ = μ(1 + 0,152p₁/p);

для прямоугольных отверстий

μ₁ = μ(1 + 0,128p₁/p),

где

μ– коэффициент расхода при полном сжатии; p₁– часть периметра, на котором нет сжатия; p – полный периметр отверстия.

16.2.. Отверстие затопленное

Рассматривая малое отверстие в тонкой стенке, из которого происходит истечение под уровень жидкости (рис. 16.2.1.)

Рис. 16.2.1.

Давления на свободные поверхности жидкости в резервуарах равны атмосферному p_а. Поверхности уровней как в правом, так и в левом резервуарах не изменяют своего положения с течением времени. Напишем уравнение Бернулли для сечений 1-1и 3-3 относительно плоскости сравнения, проходящей через центр отверстия параллельно свободным поверхностям в резервуарах.

z₁ + + = z₃+ ++h_W;

z₁ = H₁; = 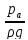; z₃ = H₂; =.

Пренебрегаем и вследствие их малости, так как площади поперечных сечений резервуаров Ω₁ ω и Ω₂ ω (ω – площадь малого отверстия).

После подстановок получим

H₁ – H₂ = h_W,

где H₁ – H₂=H; h_W = ζ_1-3 - гидравлические потери напора; ζ_1-3 - коэффициент сопротивления, учитывающий потери напора от сечения 1-1 до сечения 3-3; υ_с – средняя скорость течения в сжатом сечении с-с (2-2).

Потери напора между выбранными сечениями состоят из потерь при истечении из отверстия, т. е. от сечения 1-1 до сечения 2-2 (с-с) и от сечения 2-2

до сечения 3-3, где происходит внезапное расширение струи до существенного больших размеров

h_W = h_r0 + h_rвр.

Потери при истечении из отверстия

h_r0 = ζ .

Потери при внезапном расширении струи определяем по формуле Борда

h_rвр. = ,

где υ - скорость в резервуаре при расширении трубы, υ 0.

Потери напора

h_W = ζ + = (1 +ζ),

откуда скорость в сжатом сечении

υ_с =

или

υ_с = 𝜑.

Формула расхода для сжатого сечения при истечении через затопленное отверстие

Ω = ω_сυ_с = εφω = μω.

Полученная формула расхода аналогична формуле расхода для незатопленного отверстия. Различие формул заключается в том, что напор истечения H выражает разность уровней жидкости в резервуарах H₁ – H₂.

Установлено при проведении многочисленных опытов, что значения μ, φ для затопленного и незатопленного отверстий практически одинаковы. Поэтому в случае определения расхода или скорости через затопленное отверстие коэффициенты принимаются такими же, как и для незатопленного отверстия. На основании опытов разных авторов А. Альшулем был создан график коэффициентов φ, ε, μ в зависимости от числа Рейнольдса для малых круглых отверстий (рис. 16.2.2.).

Рис. 16.2.2.

16. 3. Истечение жидкости через большие отверстия

Отверстия являются большими, когда давление в пределах его живого сечения переменно, а скорость увеличивается по мере удаления от верхней кромки отверстия. Рассмотрим большое отверстие произвольной формы в тонкой стенке (рис. 16.3.1.).

Рис. 16.3.1.

Напор на верхней кромке отверстия H₁, по нижней – H₂. Выделим в большом отверстии горизонтальную полоску высотой dH, которую будем считать как площадь малого отверстия. Напор для такого отверстия полагаем постоянным и равным H. Элементарный расход, проходящий через эту горизонтальную полоску, шириной b (H)

dΩ = μb(H)dH,

где μ – коэффициент расхода условно малого отверстия в виде полоски; H- напор для малого отверстия.

Полагая, что μ = const для всех узких горизонтальных полосок, на которые разбивается большое отверстие.

Расход, проходящий через все горизонтальные полоски, получаем, интегрируя dΩ, а постоянные величины вынесем за знак интеграла

Ω = μdH.

При нахождении расхода по последней формуле необходимо знать функциональную зависимость переменной ширины b(H), зависящей от высоты большого отверстия.

Рассмотрим частный случай большого отверстия прямоугольной формы (рис. 16.3.2.).

Рис. 16.3.2.

Расход жидкости для прямоугольного отверстия согласно последней зависимости после интегрирования

Ω = μbdH=μb (-.

Расход жидкости может быть также вычислен, приняв напор истечения относительно центра тяжести большого отверстия, прямоугольного или круглого отверстий

Ω = μω

или

Ω = μ₀ω,

где μ₀ = μ- коэффициент расхода большого отверстия; H_с – расстояние от свободной поверхности жидкости в резервуаре до центра тяжести большого отверстия.

Для прямоугольного отверстия площадь отверстия ω = ab,

где a, b – высота и ширина отверстия.

Следует отметить, что коэффициент расхода μ₀ зависит от размеров, формы отверстия, обработки кромок отверстия, влияния стенок на сжатие струи, напора H_с и т. д.

При   расчете   больших   отверстий   значения   коэффициентов  расхода, рекомендованных Н. Н. Павловским, приведены в таблице: