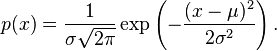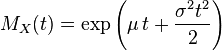- •Раздел 1. Общеобразовательные дисциплины
- •Раздел 2. Специальные дисциплины
- •Раздел 1. Общеобразовательные дисциплины
- •1.Основные понятия теории вероятностей. Случайные события, случайные величины. Функция распределения вероятностей, плотность распределения вероятностей.
- •2.Среднее значение (момента) случайных величин. Математическое ожидание, дисперсия.
- •3. Характеристическая функция случайных величин.
- •4. Нормальное (Гауссовское) распределение случайных величин. Плотность распределения и характеристическая функция момента.
- •5. Независимость случайных величин. Совместное распределение двух случайных величин. Условное распределение.
- •6. Семиуровневая модель osi/iso (гост р исо/мэк 7498-1-99).
- •Взаимодействие уровней модели osi
- •Уровень представления данных (Presentation layer)
- •Сеансовый уровень (Session layer)
- •Транспортный уровень (Transport Layer)
- •Сетевой уровень (Network Layer)
- •Канальный уровень (Data Link)
- •Физический уровень (Physical Layer)
- •7. Технико-экономические аспекты создания программного обеспечения вс. Оценка стоимости программной разработки.
- •8. Распределение затрат по фазам и видам работ программной разработки.
- •9. Компилятор в языках высокого уровня. Функции. Виды компиляторов.
- •Функции
- •Компиляторы
- •10. Ассемблер. Основные языковые конструкции. Необходимость двухпроходной трансляции. Основные работы, выполняемые транслятором. Таблицы транслятора.
- •11. Формальный язык. Грамматика. Сентенциальная форма. Нисходящий и восходящий анализ.
- •Грамматика
- •12. Понятие алгоритма и его свойства. Нормальные алгоритмы Маркова.
- •13. Иерархия запоминающих устройств. Кэш-память. Работа с кэш-памятью.
- •14. Прерывания. Классификация прерываний. Организация обработки прерываний.
- •15. Виды параллелизма. Векторная и конвейерная обработка. Классификация вычислительных комплексов по сочетанию потоков данных и потоков команд.
- •16. Информационная интегрированная среда предприятия. Общая база данных об изделиях (обди). Разделы обди.
- •17. Электронный документ. Технический электронный документ: форма представления, виды, жизненный цикл.
- •18. Электронная цифровая подпись. Суть и процесс использования электронной цифровой подписи.
- •19. Автоматизированные информационные системы. Цели и методы автоматизации.
- •20. Автоматизированные информационные системы. Математическое и программное обеспечение. Математическая модель. Программное изделие.
- •21. Свободное программное обеспечение: суть, области и проблемы использования.
- •22. Жизненный цикл программного обеспечения. Длительность. Состав. Стадии сопровождения.
- •Раздел 2. Специальные дисциплины
- •1. Модуль в языке System Verilog. Определение модуля, его применение. Задание портов и параметров.
- •2. Типы данных. Wire, reg, logic. Массивы. Строковый тип. Задание числе (в двоичном, десятичном, шестнадцатиричном виде).
- •3. Примитивы, типы примитивов. Объявление и применение примитивов.
- •4. Процедурные блоки (initial и always). Операторы управления временем.
- •Управление временем
- •5. Процедурные операторы. Операторы условного перехода. Операторы цикла. Операторы назначения. Оператор непрерывного назначения.
- •6. Маршрут проектирования программ плис. Средства разработки и проверки. Структура плис. Временные задержки сигналов
- •7. Математическое, программное и информационное обеспечение сапр. Математическая модель. Программное изделие.
- •8. Виды обеспечений, типы подсистем сапр. Общие требования к типовым сапр рэа.
- •9. Принципы измерения вектора движения ка
- •10. Геоцентрическая инерциальная система координат. Прямоугольные, сферические и геодезические координаты
- •11. Классификация орбит ка по параметрам движения. Параметры орбиты по Кеплеру.
- •12. Четыре основных свойства по.
- •13. Каскадная и спиральная модель жизненного цикла программного обеспечения
- •V модель (разработка через тестирование)
- •14. Биологический нейрон. Математическая модель нейрона. Связь искусственных нейронных сетей (инс) с другими дисциплинами. Проблемы, решаемые в контексте инс.
- •15. Архитектура нейронных сетей. Однослойный персептрон. Функции активации. Многослойный персептрон.
- •16. Понятие обучения. Методы обучения. Обучение персептрона. Процедура обратного распространения.
- •Метод к- ближайших соседей
- •Процедура обратного распространения
- •17. Гипотеза Хебба. Гипотеза ковариации. Конкурентное обучение.
- •18. Понятие vc-измерения (Вапника-Червоненкиса). Оценки обобщающей способности в задаче классификации. Теорема об универсальной аппроксимации.
- •19. Сети с локальным базисом. Сравнение сетей rbf с многослойным персептроном.
- •20. Сети Кохонена. Формализация задачи классификации для сети Кохонена. Алгоритм классификации для сети Кохонена.
- •21. Обучение Больцмана. Стохастические модели. Правило обучения Больцмана. Машина Больцмана.
- •22. Нейрокомпьютеры. Основные понятия. Классификация нейрокомпьютеров.
- •1. Что такое нейрокомпьютер?
- •2. Нейронные сети - основные понятия и определения
- •3. Модели нейронных сетей
- •3.1. Модель Маккалоха
- •3.2. Модель Розенблата
- •3.3. Модель Хопфилда
- •3.4. Модель сети с обратным распространением
- •4. Задачи, решаемые на основе нейронных сетей
- •5. Способы реализации нейронных сетей
- •6. Выводы
4. Нормальное (Гауссовское) распределение случайных величин. Плотность распределения и характеристическая функция момента.
Нормальное распределение, также называемое распределением Гаусса, — распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике. Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех.Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений, в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.
Нормальное распределение зависит от двух параметров —смещения и масштаба, то есть, является, с математической точки зрения, не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).
Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием 0 и стандартным отклонением 1.
|
Плотность вероятности
Зелёная линия соответствует стандартному нормальному распределению | |
|
Функция распределения
Цвета на этом графике соответствуют графику наверху | |
|
Параметры |
|
|
Носитель |
|
|
Плотность вероятности |
|
|
Функция распределения |
|
|
Математическое ожидание |
|
|
Медиана |
|
|
Дисперсия |
|
|
Производящая функция моментов |
|
|
Характеристическая функция |
|
Source: Нормальное (Гауссовсое) распределение
Дополнение: Предельная центральная теорема, момент случайной величины, тоже самое с другими распределениями
5. Независимость случайных величин. Совместное распределение двух случайных величин. Условное распределение.
В
одном и том же случайном эксперименте
можно рассматривать не одну, а несколько
- n - числовых функций, определенных на
одном и том же пространстве элементарных
событий. Совокупность таких функций
называется многомерной случайной
величиной или случайным вектором и
обозначается
![]() .
.
Точнее.
На вероятностном пространстве
![]() заданы случайные величины
заданы случайные величины
![]() ;
каждому w
;
каждому w
![]() W эти величины ставят в соответствие
n-мерный вектор
W эти величины ставят в соответствие
n-мерный вектор
![]() ,
который называется n-мерным
случайным вектором
(n-мерной случайной величиной).
,
который называется n-мерным
случайным вектором
(n-мерной случайной величиной).
Функцией
распределения случайного вектора
![]() или совместным распределением случайных
величин
или совместным распределением случайных
величин
![]() называется функция, определенная
равенством
называется функция, определенная
равенством
![]() ,
где
,
где
![]() .
.
По
известной многомерной функции
![]() можно найти распределение каждой из
компонент
можно найти распределение каждой из
компонент
![]() .
.
Например,
если
![]() - двумерная случайная величина, имеющая
совместное распределение
- двумерная случайная величина, имеющая
совместное распределение![]() ,
то распределения компонент
,
то распределения компонент
![]() и
и
![]() вычисляются соответственно по формулам:
вычисляются соответственно по формулам:
![]() ,
,
![]() .
.
Условным
законом распределения величины
![]() ,
входящей в систему
,
входящей в систему
![]() ,
называется ее закон распределения,
вычисленный при условии, что другая
случайная величина
,
называется ее закон распределения,
вычисленный при условии, что другая
случайная величина
![]() приняла определенное значение
приняла определенное значение
![]() .
.
Условный
закон распределения можно задавать как
функцией распределения, так и плотностью.
Условная функция распределения
обозначается
![]() условная плотность распределения
условная плотность распределения
![]() .
.
При изучении систем случайных величин всегда следует обращать внимание на степень и характер их зависимости. Эта зависимость может быть более или менее ярко выраженной, более или менее тесной. В некоторых случаях зависимость между случайными величинами может быть настолько тесной, что, зная значение одной случайной величины, можно в точности указать значение другой. В другом крайнем случае зависимость между случайными величинами является настолько слабой и отдаленной, что их можно практически считать независимыми.
Понятие о независимых случайных величинах – одно их важных понятий теории вероятностей.
Случайная
величина
![]() называется независимой
от случайной величины
называется независимой
от случайной величины
![]() ,
если закон распределения величины
,
если закон распределения величины
![]() не зависит от того, какое значение
приняла величина
не зависит от того, какое значение
приняла величина
![]() .
.
Для
непрерывных случайных величин условие
независимости
![]() от
от
![]() может быть записано в виде:
может быть записано в виде:
![]()
при
любом
![]() .
.
Напротив,
в случае, если
![]() зависит от
зависит от
![]() ,
то
,
то
![]() .
.
[
Докажем,
что зависимость или независимость
случайных величин всегда взаимны: если
величина
![]() не зависит от
не зависит от
![]() .
.
Действительно,
пусть
![]() не зависит от
не зависит от
![]() :
:
![]() .
(1)
.
(1)
Из формул (8.4.4) и (8.4.5) имеем:
![]() ,
,
откуда, принимая во внимание (1), получим:
![]()
что и требовалось доказать. ]
Так как зависимость и независимость случайных величин всегда взаимны, можно дать новое определение независимых случайных величин.
Случайные
величины
![]() и
и
![]() называются независимыми, если закон
распределения каждой из них не зависит
от того, какое значение приняла другая.
В противном случае величины
называются независимыми, если закон
распределения каждой из них не зависит
от того, какое значение приняла другая.
В противном случае величины
![]() и
и
![]() называются зависимыми.
называются зависимыми.
Для независимых непрерывных случайных величин теорема умножения законов распределения принимает вид:
![]() ,
(2)
,
(2)
т. е. плотность распределения системы независимых случайных величин равна произведению плотностей распределения отдельных величин, входящих в систему.
Условие (2) может рассматриваться как необходимое и достаточное условие независимости случайных величин.
Часто
по самому виду функции
![]() можно заключить, что случайные величины
можно заключить, что случайные величины
![]() ,
,
![]() являются независимыми, а именно, если
плотность распределения
являются независимыми, а именно, если
плотность распределения
![]() распадается на произведение двух
функций, из которых одна зависит только
от
распадается на произведение двух
функций, из которых одна зависит только
от
![]() ,
другая - только от
,
другая - только от
![]() ,
то случайные величины независимы.
,
то случайные величины независимы.
[
Пример.
Плотность распределения системы
![]() имеет вид:
имеет вид:
 .
.
Определить,
зависимы или независимы случайные
величины
![]() и
и
![]() .
.
Решение. Разлагая знаменатель на множители, имеем:
 .
.
Из
того, что функция
![]() распалась на произведение двух функций,
из которых одна зависима только от
распалась на произведение двух функций,
из которых одна зависима только от
![]() ,
а другая - только от
,
а другая - только от
![]() ,
заключаем, что величины
,
заключаем, что величины
![]() и
и
![]() должны быть независимы. ]
должны быть независимы. ]
Вышеизложенный
критерий суждения о зависимости или
независимости случайных величин исходит
из предположения, что закон распределения
системы нам известен. На практике чаще
бывает наоборот: закон распределения
системы
![]() не известен; известны только законы
распределения отдельных величин,
входящих в систему, и имеются основания
считать, что величины
не известен; известны только законы
распределения отдельных величин,
входящих в систему, и имеются основания
считать, что величины
![]() и
и
![]() независимы. Тогда можно написать
плотность распределения системы как
произведение плотностей распределения
отдельных величин, входящих в систему.
независимы. Тогда можно написать
плотность распределения системы как
произведение плотностей распределения
отдельных величин, входящих в систему.
Sources: Совместные распределения величин, Условные распределения, Зависимые и независимые распределения величин