Bilet_11
.odtЗамеча́тельные преде́лы — термин, использующийся в советских и российских учебниках по математическому анализу для обозначения некоторых широко известных математических тождеств со взятием предела. Особенно известны:
-
Первый замечательный предел:
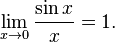
-
Второй замечательный предел:
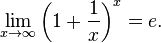
Первый замечательный предел
![]()
Доказательство
Рассмотрим односторонние
пределы ![]() и
и ![]() и
докажем, что они равны 1.
и
докажем, что они равны 1.
Пусть ![]() .
Отложим этот угол на единичной окружности
(R = 1).
.
Отложим этот угол на единичной окружности
(R = 1).
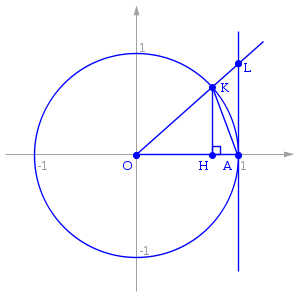
Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX.
Очевидно, что:
-
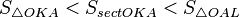 (1)
(1)
(где SsectOKA — площадь сектора OKA)
(из ![]() : | LA |
= tgx)
: | LA |
= tgx)
Подставляя в (1), получим:
Так
как при ![]() :
:
Умножаем на sinx:
Перейдём к пределу:
Найдём левый односторонний предел:
Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.
Следствия
Доказательство следствий [показать]
[править]Второй замечательный предел
![]() или
или ![]()
Доказательство второго замечательного предела:
Доказательство для натуральных значений x [показать]
![]() Зная,
что второй замечательный предел верен
для натуральных значений x, докажем
второй замечательный предел для
вещественных x, то есть докажем, что
Зная,
что второй замечательный предел верен
для натуральных значений x, докажем
второй замечательный предел для
вещественных x, то есть докажем, что ![]() .
Рассмотрим два случая:
.
Рассмотрим два случая:
1.
Пусть ![]() .
Каждое значение x заключено между двумя
положительными целыми числами:
.
Каждое значение x заключено между двумя
положительными целыми числами: ![]() ,
где
,
где ![]() —
это целая часть x.
—
это целая часть x.
-
Отсюда
следует:
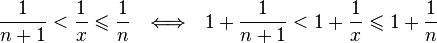 ,
поэтому
,
поэтому -
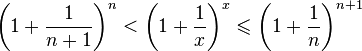 .
. -
Если
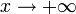 ,
то
,
то  .
Поэтому, согласно пределу
.
Поэтому, согласно пределу 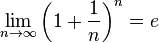 ,
имеем:
,
имеем: -
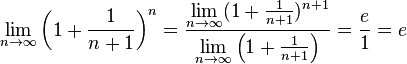
-
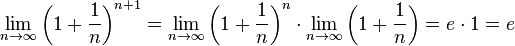 .
. -
По
признаку (о пределе промежуточной
функции) существования пределов
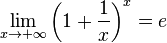 .
.
2.
Пусть ![]() .
Сделаем подстановку − x = t,
тогда
.
Сделаем подстановку − x = t,
тогда
-
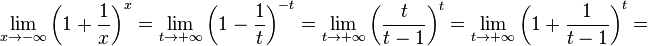
-
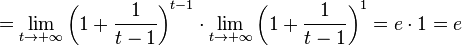 .
.
Из
двух этих случаев вытекает, что ![]() для
вещественного x.
для
вещественного x. ![]()
Следствия
-
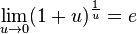
-
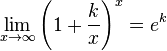
-
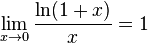
-
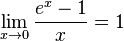
-
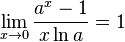 для
для 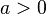 ,
, 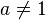
-
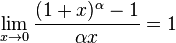

![\lim_{x \to 0-}\frac{\sin x}{x} =\left [ \begin{matrix} u = -x \\ x = -u \\ u \to 0+ \\ x \to 0-\end{matrix} \right ] =\lim_{u \to 0+}\frac{\sin(-u)}{-u} =\lim_{u \to 0+}\frac{-\sin(u)}{-u} =\lim_{u \to 0+}\frac{\sin(u)}{u} = 1](/html/25103/187/html_tOo2J0T4Eq.VKZC/img-w76DRe.png)