Глава 9

ДЛИНА

Перейдем теперь от понятия времени к другому основному понятию физики – длине, и рассмотрим его более подробно, чем мы делали до сих пор. Вспомните, что в главе 7 мы рассматривали длину как экстенсивную величину, измеряемую посредством трехчленной схемы. Правило 1 определяет эквивалентность: отрезок, отме­ченный на одном ребре, имеет равную длину с другим отрезком на другом ребре, если конечные точки этих отрезков могут быть совмещены друг с другом. Правило 2 определяет аддитивность: если мы соединим два ребра по прямой, то их общая длина будет равна сумме их отдельных длин. Правило 3 характеризует единицу дли­ны: мы выбираем стержень с прямым ребром, отмечаем две точки на этом ребре и берем отрезок между двумя этими точками в качестве нашей единицы длины.

Рис. 9-1.

Основываясь на этих трех правилах, мы можем те­перь применить обычную процедуру измерения. Пред­положим, что мы хотим измерить длину длинного края c, скажем, края ограды. Мы имеем измерительный стер­жень, на котором наша единица длины отмечена конеч­ными точкамиAиB. Мы располагаем стержень вдольcв положенииa₁(см. рис. 9-1), так чтоAсовпадет с одной из конечных точекC₀наc.На крае оградыcмы отметим точкуC₁, которая совпадет с концомBнашего стержня. Затем мы передвигаем стерженьaв смежную

137

позицию a₂и отмечаем точкуC₂.наcи т.д., пока мы не достигнем другого концаc. Предположим, что десятая позицияa₁₀стержня такова, что его конечная точкаB приблизительно совпадет с конечной точкойC₁₀c. Пустьc₁,c₂, ...,c₁₀будут отмеченными отрезкамиc.По правилу 3 мы имеем

.

Таким образом, по правилу 1, эквивалентности:

.

По правилу 2, аддитивности:

Следовательно,

.

Эта процедура, являющаяся основной процедурой для измерения длины, в качестве значений измеряемой длины дает только целые числа. Очевидное уточнение достигается посредством деления единицы длины на n равных частей. (Дюйм традиционно делится последова­тельно пополам: сначала на две части, затем на четыре, восемь и т.д. Метр делится на десять последовательных частей: сначала на десять, затем на сто и г. д.) Таким образом мы в состоянии построить, путем проб и оши­бок, вспомогательный измерительный стержень, разде­ленный на отрезки длиныd,таких, чтоdможет быть отложено вдоль единичного ребраa в nсмежных пози­цияхd₁,d₂, …,d_n(см. рис. 9-2).

Рис. 9-2.

Мы можем теперь сказать, что

.

138

 

Следовательно:

.

С помощью этих частей отрезков, отложенных на a, мы можем теперь более точно измерить длину данного ребра. Когда мы снова измерим длину оградыcв пре­дыдущем примере, то может оказаться, что эта длина равна не 10, а более точно 10,2. Таким способом вво­дятся в измерение дроби. Мы больше не ограничиваемся целыми числами. Измеряемое значение может быть лю­бым положительным рациональным числом.

Важно понять, что, делая такие уточнения при изме­рении, мы можем вводить все меньшие и меньшие дроби, но мы никогда не придем к числам, которые не были бы рациональными. С другой стороны, класс возможных значений величин в физике обычно рассматривается как содержащий все действительные числа (или все дейст­вительные числа определенного интервала), куда входят как иррациональные, так и рациональные числа. Однако иррациональные числа вводятся на более поздней ста­дии, чем измерение. Непосредственное измерение может дать только значения, выражаемые с помощью рацио­нальных чисел. Но когда мы формулируем законы и делаем вычисления с помощью этих законов, тогда на сцену выступают иррациональные числа. Они вводятся не в процессе измерения, а в теоретическом контексте.

Чтобы сделать это яснее, рассмотрим теорему Пифа­гора, которая утверждает, что квадрат гипотенузы равен сумме квадратов катетов. Это теорема геометрии, но когда мы применяем ее к физическим отрезкам, она становится также физическим законом. Предположим, что мы вырезали из деревянной доски квадрат со стороной, равной единице длины. Теорема Пифагора говорит нам, что длина диагонали этого квадрата (рис. 9-3) равна квадратному корню из 2. Квадратный корень из 2 пред­ставляет иррациональное число. Поэтому диагональ квадрата не может быть измерена с помощью линейки совершенно точно, независимо от того какие мелкие доли единицы измерения мы выберем. Однако когда мы используем теорему Пифагора, чтобы вычислить длину

139

 

диагонали, то мы косвенно получим иррациональное число.

Рис. 9-3.

Подобным же образом, если мы измерим диаметр круглого деревянного диска и найдем, что он будет равен 1, тогда с помощью вычисле­ния мы обнаружим, что длина ок­ружности диска будет равна ирра­циональному (пи).

Поскольку иррациональные чис­ла всегда получаются в результате вычислений, а не непосредственных измерений, то нель­зя ли и в физике совершенно отказаться от иррацио­нальных чисел и оперировать только рациональными числами? Это, конечно, возможно, но это было бы ре­волюционным изменением. Мы, например, были бы не в состоянии больше работать с дифференциальными уравнениями, потому что такие уравнения требует кон­тинуума действительных чисел. Физики, однако, не на­ходят достаточных оснований для подобных изменений. Верно, однако, что в квантовой физике мы с самого на­чала обнаруживаем тенденцию к дискретности. Напри­мер, электрический заряд измеряется только в величинах, которые представляют кратное минимального электриче­ского заряда.

Если мы возьмем этот минимальный заряд как еди­ницу, тогда все значения электрических зарядов будут представляться целыми числами. Квантовая механика не является все же полностью дискретной, но она на­столько дискретна, что некоторые физики с самого на­чала выдвигают предположение о возможной дискрет­ности всех физических величин, включая пространство и время. Это только предположение, хотя и наиболее ин­тересное.

Какого рода законы будут возможны в такой фи­зике? Там будет, вероятно, минимальное значение для каждой величины, а все большие значения будут выра­жаться как кратные этого основного значения. Мини­мальное значение для длины предлагали назвать «ходоном», а для времени – «хрононом». Дискретное время будет состоять из непостижимых мгновенных скачков, подобных движению стрелки электрических часов, когда она перескакивает от одной секунды к другой. Никакое

140

 

физическое событие не может произойти в пределах лю­бого интервала между скачками.

Рис. 9-4.

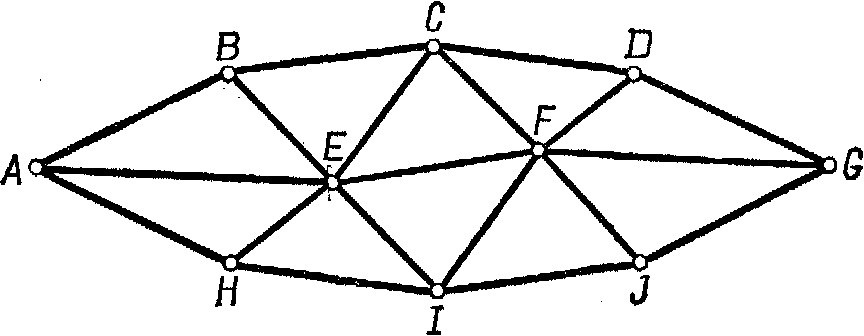
Дискретное пространство может состоять из точек такого рода, которые показаны на рис. 9-4. Линии, сое­диняющие их на рисунке, показывают, какие точки являются «соседними точками» (например, BиC– сосед­ние точки, аBиF – нет). В обычной геометрии непре­рывного мы должны говорить, что существует бесконечное множество точек междуBиC, но в дискретной гео­метрии, если физика придерживается этого взгляда на пространство, мы обязаны сказать, что междуBиCне существует никаких промежуточных точек. Никакое физическое явление какого-либо рода не может нахо­диться в позиции «между»BиC. Например, электрон будет находиться в одной из точек сетки, а не где-либо еще на диаграмме. Длина будет определяться как ми­нимальное расстояние, связывающее две точки. Мы мо­жем условиться считать расстояние между двумя сосед­ними точками равным 1. Тогда длина путиABCDGбудет равна 4,aAEFG – 3. Мы будем говорить, что расстоя­ние отAдоGравно 3, потому что оно представляет кратчайший путь отAдо G. Каждая длина будет выра­жаться целым числом. Фактически никакой системы такого рода не было построено для физики, хотя многие предварительные наметки и были сделаны. Некоторые физики размышляли даже о размерах этих минималь­ных величин.

Когда-то в будущем, когда мы гораздо больше будем знать о пространстве и времени и других величинах фи­зики, возможно, что мы обнаружим, что все они яв­ляются дискретными. Тогда законы физики будут иметь дело исключительно с целыми числами. Они будут,

141

 

конечно, целыми числами огромных размеров. В милли­метре длины, например, будут содержаться биллионы минимальных единиц. Значения, принимаемые величи­нами, будут так близки друг к другу, что практически мы можем поступать с ними так, как если бы мы имели континуум действительных чисел. Практически физики, вероятно, будут продолжать пользоваться дифференци­альными и интегральными исчислениями и формулиро­вать законы в виде дифференциальных уравнений так же, как и прежде. Самое большее, что мы можем сказать теперь, – это то, что некоторые особенности физики бла­годаря принятию дискретной шкалы станут проще, в то время как другие значительно усложнятся.

С помощью наших наблюдений мы никогда не можем решить, должно ли быть выражено значение величины рациональным или иррациональным числом, поэтому этот вопрос является целиком вопросом удобства: бу­дет ли наиболее полезной для формулировки некоторых физических законов дискретная или непрерывная шкала чисел?

Описывая, как могут быть измерены длины, мы до сих пор не рассматривали один крайне важный вопрос: какого рода тело мы должны взять в качестве стандарт­ной измеряющей линейки (стержня)? Для повседневных целей достаточно будет взять железную или даже дере­вянную линейку, потому что здесь нет необходимости измерять длины с большой точностью. Но, если мы стре­мимся к большой точности, то сразу же увидим, что здесь мы встречаемся с трудностью, подобной той, с ко­торой мы сталкивались в отношении периодичности.

Как вы помните, раньше перед нами стояла пробле­ма – построить нашу единицу времени с помощью пе­риодических процессов с равными периодами. Здесь мы сталкиваемся с аналогичной проблемой основания нашей единицы длины с помощью «твердого тела». Мы склон­ны думать, что мы нуждаемся в теле, которое всегда со­храняло точно ту же самую длину; так же как прежде мы нуждались в периодическом процессе с временными интервалами, которые были бы всегда одинаковыми. Очевидно, мы не хотим основывать нашу единицу длины на резиновой линейке или линейке, сделанной из воска, которые легко изменяют свою форму. Мы предполагаем, что мы нуждаемся в твердой линейке, которая не изменяла

142

бы свою форму и размеры. Возможно что мы определим «твердость» следую­щим образом: линейка является твердой, если расстояние между двумя отметками, сделанными на ней, остается постоянным с течением времени.

Рис. 9-5.

Но что точно мы по­нимаем под фразой «остается постоян­ным»? Для объяснения этого мы должны вве­сти понятие длины. Ес­ли бы мы не имели понятия длины и средств для ее из­мерения, то что бы означало утверждение, что расстоя­ние между двумя точками на стержне фактически оста­ется постоянным? И если мы не можем определить это, то как мы можем определить твердость? Мы, таким об­разом, попадаем здесь в ту же самую ловушку пороч­ного круга, в которой мы очутились, когда искали спо­соб распознавания сильно периодических процессов до того, как разработали систему измерения времени. Как еще раз мы можем избежать порочного круга?

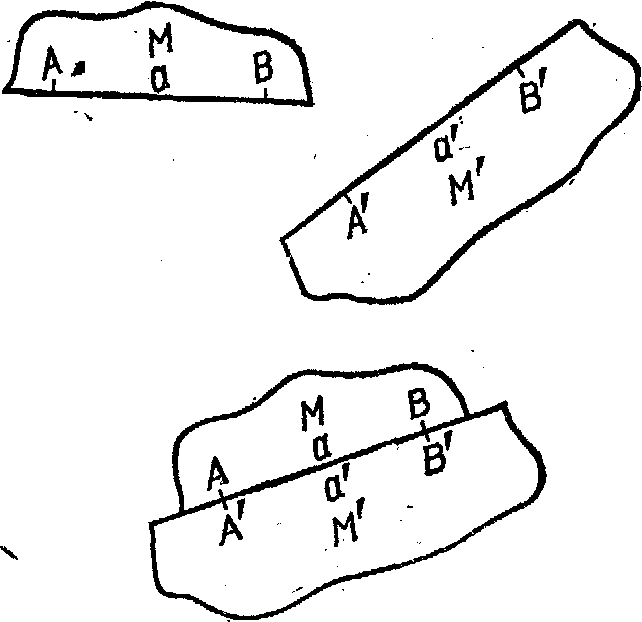
Выход из него подобен тому способу, с помощью которого мы избежали порочного круга при измерении времени: использование относительных понятий вместо абсолютных. Мы можем без всякого логического круга определить понятие «относительной твердости» одного тела по отношению к другому. Возьмем одно тело Mи другоеW.Ради простоты мы будем предполагать, что каждое из них имеет прямое ребро. Мы можем совме­стить эти ребра и сравнить точки, отмеченные на них (рис. 9-5).

Рассмотрим пару точек A,BнаM, которые опреде­ляют отрезокa.Аналогичным образом наM'возьмем пару точекA'иB',которые определяют отрезокa'.Мы скажем, что отрезокaравен (конгруентен) отрезкуa, вели всякий раз, когда два ребра совмещаются друг с другом и точкаAсовпадает с точкойA',то точкаB

143

 

совпадает с точкой B'.Такова наша операциональная про­цедура для определения того, что отрезкиaиa'равны. Всякий раз, когда мы делаем такую проверку и находим, что соответствующие пары точек совпадают, мы заклю­чаем, что при повторении эксперимента в любое время в будущем его результат, вероятно, будет тот же самый. Дополнительно к этому предположим, чтокаждыйотре­зок, отмеченный таким способом наM,будет равен со­ответствующему отрезку наM'в любое время, когда осуществляется проверка. Мы тогда скажем, чтоM и M' являютсятвердыми относительно друг друга.

Важно осознать, что никакого логического круга здесь не возникает. Мы не можем и не говорим об абсо­лютной твердости M.Мы не можем сказать, чтоMвсег­да сохраняет свою длину. Однако имеет смысл говорить, что два тела являются твердымив отношении друг к другу.Если мы выберемMв качестве измеряющего стержня, то мы обнаружим, что отрезки, отмеченные наM',остаются постоянными по длине. Если в качестве из­меряющего стрежня мы выберемM',то постоянными по длине остаются отрезки наM.То, что мы здесь имеем, – это понятие относительной твердости, твердости одного тела по отношению к другому.

Когда мы испытываем различные тела в мире, то мы находим, что многие из них не являются твердыми друг относительно друга. Рассмотрим, например, две моих руки. Я свожу их вместе так, что некоторые пары точек на кончиках моих пальцев совпадают. Затем я их сво­жу снова. Положение моих пальцев изменится. Те же самые пары точек больше уже не будут совпадать, по­этому я не могу сказать, что мои руки будут твердыми относительно друг друга. То же самое будет верно, если мы сравним два тела, сделанные из воска, или же одно тело из железа, а другое из мягкой резины. Они не яв­ляются твердыми друг относительно друга. Но так же, как мы находим, что в мире имеется обширный класс процессов, которые эквивалентны по своей периодич­ности, так и здесь мы сталкиваемся с другим счастливым случайным обстоятельством природы. Эмпирически мы находим, что имеется обширный класс тел, которые яв­ляются приблизительно твердыми друг относительно друга. Два любых тела из металла – железа, меди и

144

 

т. п. – являются твердыми друг относительно друга. Та­кими же являются тела из камня и даже дерева, если они достаточно сухие и не покрыты зеленью. Мы нахо­дим, что огромное количество твердых веществ отно­сится к тому роду, что тела, сделанные из этих веществ, являются твердыми друг относительно друга. Конечно, они не будут твердыми, если согнем их или заставим расширяться путем нагревания и т.п. Но если никакие ненормальные условия не накладываются, то эти тела в отношении их длин ведут себя весьма регулярным образом. Когда мы производим грубое сравнение одного тела с другим, мы находим их относительно твер­дыми.

Вы помните, что при обсуждении периодичности мы видели, что не существует никакого логического основа­ния, заставляющего нас строить измерение времени на каком-либо одном периодическом процессе, принад­лежащем к обширному классу эквивалентных процессов. Мы выбираем такой процесс только потому, что он при­водит к большей простоте наших законов природы. Ана­логичный выбор имеется и здесь. Нет никакой логиче­ской необходимости основывать измерение длины на од­ном определенном классе, взятом из обширного класса относительно твердых тел. Мы выбираем такие тела по­тому, что с ними более удобно иметь дело. Если бы мы выбрали в качестве единицы измерения стержень, сде­ланный из резины или воска, то мы бы могли найти в мире очень немного (если ни одного) тел, которые были бы относительно твердыми по нашему стандарту. Наше описание природы стало бы, таким образом, чрез­вычайно сложным. Мы должны были бы тогда, напри­мер, говорить, что железные тела постоянно изменяют свою длину, потому что каждый раз, когда мы измеряем их нашей гибкой резиновой линейкой, мы получаем раз­личные значения. Ни один ученый, конечно, не захочет обременять себя изобретением сложных физических за­конов, чтобы описать такие явления: С другой стороны, если мы выберем в качестве единицы длины металличе­скую полоску, то мы обнаружим в мире очень большое число твердых тел, когда они измеряются этой единицей. Благодаря этому в наше описание мира вводятся бо́льшая регулярность и простота.

145

 

Эта регулярность возникает, конечно, из природы действительного мира. Мы могли бы жить в мире, в ко­тором железные тела были бы твердыми друг относи­тельно друга, а медные тела, в свою очередь, были бы твердыми относительно друг друга, но железные тела были бы нетвердыми по отношению к медным. Здесь не существует никакого логического противоречия. Это один из возможных миров. Если бы мы жили в таком мире и обнаружили, что он содержит много железа и меди, то какой из этих металлов мы бы выбрали в качестве под­ходящей основы для измерения? Каждый выбор имел бы определенные недостатки. Если же другие металлы подобным же образом, так сказать, не соответствовали друг другу, то такой выбор было бы сделать гораздо трудней. К счастью, мы живем в мире, где это не имеет места. Все металлы являются твердыми друг относитель­но друга. Таким образом, мы можем взять любой из них в качестве нашего стандарта. Когда мы это сделаем, мы обнаружим, что другие металлические тела являются твердыми.

Вот почему, очевидно, желательно пользоваться при измерении длины скорее металлическим, чем резиновым стержнем, а при измерении времени – скорее маятни­ком, чем биениями пульса. Мы склонны забывать, что имеется конвенциональный элемент в нашем выборе стандарта для измерения. Наличие этого элемента я под­черкивал в моей докторской диссертации о простран­стве^14[6], а Рейхенбах позже отмечал в своей книге о про­странстве и времени^15[7]. Выбор является условным (кон­венциональным) в том смысле, что не существует ни­какого логического основания запретить нам выбрать в качестве стандарта резиновый стержень и биения пульса, но за это нам придется расплачиваться разра­боткой фантастически сложной физики, чтобы иметь дело с миром, в котором господствует иррегулярность. Это, конечно, вовсе не означает, что выбор является про­извольным, что один выбор является таким же хорошим, как и другой. Существуют сильные практические основания,

146

 

связанные с природой мира, для того, чтобы предпочесть стальной стержень и маятник.

Как только мы выберем стандарт для измерения, такой, как металлический стержень, мы сталкиваемся с другим выбором. Мы можем сказать, что длина данного конкретного стержня служит единицей измерения независимо от изменения его температуры, магнетизма и т.п., или же мы можем ввести поправочные коэффи­циенты, зависящие от таких изменений. Первый выбор, очевидно, дает более простые правила, но если мы сде­лаем его, то снова столкнемся со странными следст­виями. Если стержень нагревается и затем используется для измерения, то мы обнаружим, что все другие тела в мире сократятся. Когда стержень охладится, осталь­ной мир снова расширится. Мы будем вынуждены сфор­мулировать всякого рода причудливые и сложные за­коны, но здесь не будет никакого логического противоре­чия. По этим основаниям мы можем говорить о возмож­ном выборе.

Вторая процедура связана с введением поправочных коэффициентов. Вместо условия, что отрезок между двумя отметками будет рассматриваться как имеющий выбранную длину l₀ (скажем, 1 или 100), мы теперь будем заявлять, что он имеет нормальную длинуl₀, только когда стержень имеет температуруT₀,которую мы выбираем в качестве «нормальной» температуры, в то время как при любой другой температуреTдлина отрезка дается уравнением

,

где есть константа (называемая «коэффициентом теплового расширения»), которая характеризует вещество стержня. Подобные же поправки таким же путем вводятся для других условий, таких, как наличие магнитных полей, которые также могут повлиять на длину стержня. Физики предпочитают больше эту более сложную процедуру – введение поправочных коэффициентов – по тем же самым основаниям, по которым они выбирают металлический стержень вместо резинового – такой выбор приводит к значительному упрощению физических законов.

147