
Вопросы_по_мат_логике_3_сем_экз_Дьячков / Logika_3_4
.docx3. Алгебра высказываний; логическая эквивалентность и логическое следствие:
Логическое равенство (эквивалентность)
Образуется
соединением двух логических выражений
с помощью оборотов «тогда и только
тогда», «необходимо и достаточно»,
«...равносильно...». Поскольку мы видим
здесь двойное следование (и вправо и
влево), операцию иногда называют двойной
импликацией. Дополнительная операция,
так как A
↔ B
= (A
\/
![]() )
& (
)
& (![]() \/ B)
\/ B)
|
A |
B |
F = A ↔ B |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
Суть: эквивалентность ложна только тогда, когда выражения разные.
Эквивалентные высказывания
Эквивалентными (тождественными или равносильными) называются высказывания, значения которых совпадают при любых значениях входящих в него переменных.
Операция “эквивалентность” обозначается по-разному. Выражения
![]()
обозначают одно и тоже, и можно сказать, что А эквивалентна В, если и только если они равнозначны. Логическая операция “эквивалентность” выражается через логические функции “И”, “ИЛИ”, “НЕ” в виде логической формулы
![]()
Логическое следование (импликация)
Связывает
два логических выражения с помощью
оборота ЕСЛИ..., ТО.
Дополнительная
операция, так как A
→ B
=
![]() \/ B
Кроме
того, при построении высказывания могут
использоваться выражения «из... следует»,
«... влечет».
\/ B
Кроме
того, при построении высказывания могут
использоваться выражения «из... следует»,
«... влечет».
|
A |
B |
F = A → B |
|
0 |
0 |
1 |
|
0 |
1 |
1 |
|
1 |
0 |
0 |
|
1 |
1 |
1 |
В таблице хорошо видна практическая суть: импликация ложна только тогда, когда первое выражение истинно, а второе ложно.
Операцию “импликация” можно обозначить по-разному:
![]()
Эти выражения эквивалентны и читаются одинаково: «Игрек равен импликации от А и В». Операция “импликация” выражается через логические функции “ИЛИ”, “НЕ” в виде логической формулы
![]()
С помощью алгебры логики можно очень кратко записать законы формальной логики и дать им математически строгое доказательство.

4. Алгебра высказываний; дизъюнктивная и конъюктивная нормальные формы:
Дизъюнктивные и конъюнктивные нормальные формы булевых функций
Определение
1. Конъюнктивным одночленом
(элементарной конъюнкцией) от переменных
![]() называется
конъюнкция этих переменных или их
отрицаний.
называется
конъюнкция этих переменных или их
отрицаний.
Например,
![]() –
элементарная конъюнкция.
–
элементарная конъюнкция.
Определение
2. Дизъюнктивным одночленом
(элементарной дизъюнкцией) от переменных
![]() называется
дизъюнкция этих переменных или их
отрицаний.
называется
дизъюнкция этих переменных или их
отрицаний.
Например,
![]() –
элементарная дизъюнкция.
–
элементарная дизъюнкция.
Определение 3. Формула, равносильная данной формуле алгебры высказываний и являющаяся дизъюнкцией элементарных конъюнктивных одночленов, называется дизъюнктивной нормальной формой (ДНФ) данной формулы.
Например,
![]() –
ДНФ.
–
ДНФ.
Определение 4. Формула, равносильная данной формуле алгебры высказываний и являющаяся конъюнкцией элементарных дизъюнктивных одночленов, называется конъюнктивной нормальной формой (КНФ) данной формулы.
Например,
![]() –
КНФ.
–
КНФ.
Для каждой формулы алгебры высказываний можно найти множество дизъюнктивных и конъюнктивных нормальных форм.
Алгоритм построения нормальных форм
-
С помощью равносильностей алгебры логики заменить все имеющиеся в формуле операции основными: конъюнкцией, дизъюнкцией, отрицанием:
![]() ;
;
![]() ;
;
![]() .
.
-
Заменить знак отрицания, относящийся к выражениям типа
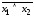 или
или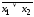 ,
знаками отрицания, относящимися к
отдельным переменным высказываниям
на основании формул:
,
знаками отрицания, относящимися к
отдельным переменным высказываниям
на основании формул:
![]() ;
;
![]() .
.
-
Избавиться от знаков двойного отрицания.
-
Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.
Совершенная дизъюнктивная и совершенная конъюнктивная нормальные формы
Любая булева функция может иметь много представлений в виде ДНФ и КНФ. Особое место среди этих представлений занимают совершенные ДНФ (СДНФ) и совершенные КНФ (СКНФ).
Определение
1. Совершенная дизъюнктивная
нормальная форма (СДНФ) – это ДНФ, в
которой в каждый конъюнктивный одночлен
каждая переменная
![]() из
набора
из
набора![]() входит
ровно один раз, причем входит либо сама
входит
ровно один раз, причем входит либо сама![]() ,
либо ее отрицание
,
либо ее отрицание![]() .
.
Конструктивно СДНФ для каждой формулы алгебры высказываний, приведенной к ДНФ, можно определить следующим образом:
Определение 2. Совершенной дизъюнктивной нормальной формой (СДНФ) формулы алгебры высказываний называется ее ДНФ, обладающая следующими свойствами:
-
ДНФ не содержит двух одинаковых конъюнкций;
-
ни одна конъюнкция не содержит одновременно двух одинаковых переменных;
-
ни одна конъюнкция не содержит одновременно некоторую переменную и ее отрицание;
-
каждая конъюнкция содержит либо переменную
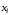 ,
либо ее отрицание
,
либо ее отрицание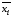 для
всех переменных, входящих в формулу.
для
всех переменных, входящих в формулу.
Определение
3. Совершенная конъюнктивная
нормальная форма (СКНФ) – это КНФ, в
которой в каждый дизъюнктивный одночлен
каждая переменная
![]() из
набора
из
набора![]() входит
ровно один раз, причем входит либо сама
входит
ровно один раз, причем входит либо сама![]() ,
либо ее отрицание
,
либо ее отрицание![]() .
.
Конструктивно СКНФ для каждой формулы алгебры высказываний, приведенной к КНФ, можно определить следующим образом.
Определение 4. Совершенной конъюнктивной нормальной формой (СКНФ) данной формулы алгебры высказываний называется такая ее КНФ, которая удовлетворяет следующим свойствам.
-
КНФ не содержит двух одинаковых дизъюнкций.
-
Ни одна конъюнкция не содержит одновременно двух одинаковых переменных.
-
Ни одна из дизъюнкций не содержит одновременно некоторую переменную и ее отрицание.
-
Каждая дизъюнкция СКНФ содержит либо переменную
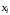 ,
либо ее отрицание
,
либо ее отрицание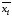 для
всех переменных, входящих в формулу.
для
всех переменных, входящих в формулу.
