
Вопросы_по_мат_логике_3_сем_экз_Дьячков / 1_I_2_Voprosy_Po_Mat_Logike
.docx-
Алгебра высказываний; пропозициональные связки и формы, истинностные таблицы.
Под высказыванием мы понимаем повествовательное предложение, которому мы можем приписать истинностное значение «истина» или «ложь». «Истина» обозначается цифрой 1, а «ложь» цифрой 0. Сами высказывания обозначаются заглавными латинскими буквами.
Для отражения и формализации связок между высказываниями на мат. уровне вводятся операции над высказываниями. Определить каждую операцию – значит приписать истинностное значение результату операции в зависимости от истинностных значений ее аргументов. Для этого удобны истинностные таблицы.
Операции:
-
Отрицание ⌐А (или Ā) высказывания А. («не А»)

-
Конъюнкция АꓥВ (А&В или А*В) высказываний А и В. («и А, и В»)
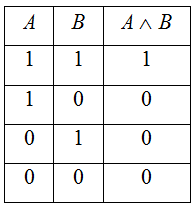
-
Дизъюнкция АꓦВ высказываний А и В. («А или В»)
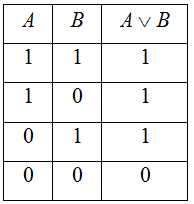
-
Импликация А→И высказываний А и В. («если А, то В»)
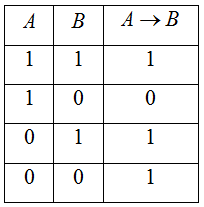
-
Эквивалентность А≡В высказываний А и В. («А тогда и только тогда, когда В»)

Символы ⌐, ꓥ, ꓦ, →, ≡ называются пропозициональными (или логическими) связками. Осмысленные формулы, составленные из высказываний (пропозициональных букв), пропозициональных связок, а также скобок называются пропозициональными формами (ПФ). Обозначаются ПФ рукописными латинскими буками.
Пример.
B
=
![]()
Если в какой-то части ПФ пропущены скобки, то операции выполняются в следующем порядке: ⌐, ꓥ, ꓦ, →, ≡
Используя истинностные таблицы для пропозициональных связок, можно получить истинностную таблицу для произвольной ПФ.
Пример. 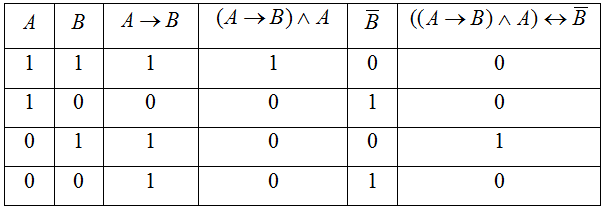
![]()
-
Алгебра высказываний; тавтологии и противоречия
Если ПФ принимает значение 1 на любом истинностном наборе, то эта ПФ называется тавтологией. Если же ПФ принимает значение 0 на любом истинностном наборе, то эта ПФ называется противоречием. Если ПФ не является противоречием, то называется выполнимой. Из тавтологий получаются высказывания, истинные по форме, а из противоречий ложные по форме (но не по содержанию).
Примеры тавтологий: Аꓦ⌐А (закон исключенного третьего), А≡⌐⌐А (закон двойного отрицания), А→АꓦВ, АꓥВ→А, А→В≡⌐АꓦВ
Примеры противоречий: Аꓥ⌐А, А≡⌐А, Аꓥ⌐(АꓦВ)
-
Если B – тавтология, то ⌐B – противоречие и наоборот.
-
Если A и A→ B – тавтологии, то B - тавтология
-
Если A→B и A→⌐B - тавтологии, то A – противоречие
-
Если в тавтологию вместо пропозициональных букв подставить произвольные ПФ, то снова получится тавтология
