Вопросы_по_мат_логике_3_сем_экз_Дьячков / M@7L0g3X@m3N

13) Логическая общезначимость

Общезначимость — свойство логической формулы, состоящее в том, что эта формула истинна при любой интерпретации входящих в неё нелогических символов, то есть предикатных и пропозициональных переменных. Логические формулы, обладающие этим свойством, называют общезначимыми, или тождественно истинными, или тавтологиями. Всякая общезначимая формула выражает логический закон. Вместо слов «формула A общезначима» часто пишут: |=А{\displaystyle \vDash A}. Важнейшими видами логических формул являются пропозициональные и предикатные формулы. Общезначимость предикатной формулы означает истинность в любой модели. Множество общезначимых предикатных формул неразрешимо, то есть не существует алгоритма, позволяющего для произвольной предикатной формулы выяснить, общезначима ли она (это результат Чёрча). Из теоремы Гёделя о полноте следует, что все общезначимые предикатные формулы и только они выводимы в классическом исчислении предикатов.

Определение. Формула A называется общезначимой, если она тождественно истинная на всякой области.

Теорема. Для того, чтобы формула A была общезначима, необходимо и достаточно, чтобы ее отрицание было не выполнимо.

Доказательство

Необходимость. Пусть формула A общезначима. Тогда, очевидно, Ā – тождественно ложная формула в любой области, и поэтому формула A не выполнима.

Достаточность. Пусть формула Ā не выполнима в любой области. Тогда по определению невыполнимой формулы Ā – тождественно ложная в любой области. Значит, формула A – тождественно истинная формула в любой области, и, следовательно, она общезначима.

Общезначимые формулы играют особую роль в логике: они на языке алгебры высказываний выражают законы логики. Общезначимые формулы истинны в силу своей структуры, независимо от истинностных значений составляющих их формул. Например, для любой формулы А формульная схема АÚ¬А принимает значение И независимо от значения формулы А. В самом деле, если А=И, то дизъюнкция АÚ¬А принимает значение И. Если же А=Л, то тогда АÚ¬А=И, а дизъюнкция АÚ¬А опять принимает значение И. Рассмотренная формульная схема выражает один из законов логики - закон исключенного третьего.

При любом выборе формул А, В, С нижеследующие формульные схемы представляют собой общезначимые формулы.

Формулы (1)—(13) составляют одну из возможных полных, независимых аксиоматик логики высказываний. В то же время они являются одним из способов выражения важнейших (и простейших) схем рассуждений.

Формулы (14) и (15) позволяют равносильным образом избавляться от эквиваленции и импликаций.

В связи с формулами (21) — (26) обращаем внимание на то, что импликация не является ни коммутативной, ни ассоциативной операцией. С некоммутативностью импликации, в частности, связано наличие у нее специальных имен для первого и второго членов — антецедент и консеквент. В силу коммутативности и ассоциативности операций конъюнкции, дизъюнкции (и эквиваленции) члены этих операций можно при равносильных преобразованиях произвольным образом объединять скобками в группы, производя при необходимости требуемые перестановки. Учитывая ассоциативность конъюнкции (дизъюнкции, эквиваленции), многочленные конъюнкции (дизъюнкции, эквиваленции) можно писать без скобок.

Отметим еще, что из четырех бинарных операций конъюнкции, дизъюнкции, импликации и эквиваленции дизъюнкция и импликация дистрибутивны относительно трех остальных, конъюнкция дистрибутивна только относительно дизъюнкции, а эквиваленция не дистрибутивна ни относительно одной из остальных операций (формулы (27) - (33)).

Общезначимость каждой из 50 формул можно установить, например, составив истинностную таблицу для конкретной формулы и убедившись в том, что последний столбец каждой такой таблицы состоит только из одних И.

14) Эквивалентность формул логики предикатов

Определение. Две формулы логики предикатов A и B называются равносильными на области М, если они принимают одинаковые логические значения при всех значениях входящих в них переменных, отнесенных к области М.

Определение. Две формулы логики предикатов A и B называются равносильными, если они равносильны на всякой области.

Ясно, что все равносильности алгебры высказываний будут верны, если в них вместо переменных высказываний подставить формулы логики предикатов. Но, кроме того, имеют место равносильности самой логики предикатов. Рассмотрим основные из этих равносильностей. Пусть A(х) и B(х) – переменные предикаты, а С – переменное высказывание.

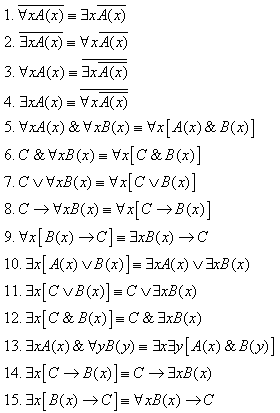
Равносильность 1 означает тот простой факт, что если не для всех х истинно A(х), то существует х, при котором будет истиной Ā (x).

Равносильность 2 означает тот простой факт, что если не существует x, при котором истинно A(х), то для всех х будет истиной Ā (x).

Равносильности 3 и 4 получаются из равносильностей 1 и 2 соответственно, если от обеих их частей взять отрицания и воспользоваться законом двойного отрицания.

Докажем равносильность 5. Если предикаты A(х) и B(х) одновременно тождественно истинные, то будет тождественно истинным и предикат A(х)& B(х), а поэтому будут истинными высказывания

"xA(x), "xB(x), "x [A(x)&B(x)],

т.е. в этом случае обе части равносильности 5 принимают значение «истина».

Пусть теперь хотя бы один из предикатов, например, A(х), будет не тождественно истинным. Тогда не тождественно истинным будет и предикат A(х)& B(x), а поэтому ложными будут высказывания

"xA(x), "xA(x)&"xB(x), "x [A(x)&B(x)],

т.е. и в этом случае обе части равносильности 5 принимают одинаковые (ложные) значения. Этим исчерпывается доказательство равносильности 5.