
Вопросы_по_мат_логике_3_сем_экз_Дьячков / Mat_Logika_9_10
.docx9). Формальная аксиоматическая теория, формализация понятий теоремы и её доказательства.
В
формальной аксиоматической теории
(ФАТ) выводом или доказательством формулы
A называется конечная цепочка формул,
каждая из которых есть либо аксиома,
либо непосредственное следствие
каких-либо из предыдущих формул по
одному из правил вывода, причем последняя
формула этой цепочки - это и есть формула
A. Если для формулы A существует вывод,
то говорят, что она является теоремой
ФАТ, и пишут так:
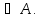
-
Пусть
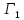 и
и
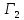 –
два множества формул, причем
–
два множества формул, причем
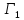 ≤
≤
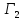 .
Тогда если
.
Тогда если
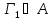 , то
, то
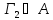 .
. -
Пусть
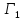 и
и
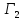 – два множества формул, причем каждая
из формул
– два множества формул, причем каждая
из формул
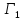 является следствием множества формул
является следствием множества формул
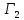 .
Тогда если
.
Тогда если
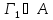 , то
, то
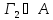 .
. -
Следствие множества теорем само является теоремой.
10). Формальная аксиоматическая теория, теорема дедукции, правило силлогизма и перестановки посылок.
(A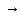 B)
B)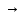 ((B
((B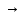 C)
C)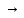 (A
(A C))
- правило силлогизма (ПС)
C))
- правило силлогизма (ПС)
(A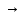 (B
(B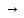 C))
C))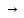 (B
(B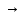 (A
(A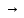 C))
- правило
перестановки посылок (ПП)
C))
- правило
перестановки посылок (ПП)
Теорема
дедукции:
Если Г,А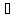 В,
то Г
В,
то Г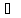 А
А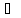 В.
В.
Доказательство.
Пусть последовательность формул B1, B2,
…,
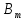 есть вывод B из Г,A. В ней
есть вывод B из Г,A. В ней
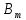 = B. Индукцией по i покажем, что Г
= B. Индукцией по i покажем, что Г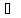 A
A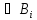 для каждого i = 1, …, m. При i = m будем иметь
утверждение теоремы. Сначала заметим,
что, по определению вывода, для каждой
формулы
для каждого i = 1, …, m. При i = m будем иметь
утверждение теоремы. Сначала заметим,
что, по определению вывода, для каждой
формулы
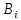 при i
при i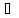 {1,
…, m} возможны следующие случаи: 1)
{1,
…, m} возможны следующие случаи: 1)
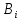 =A, 2)
=A, 2)
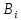 – аксиома, 3)
– аксиома, 3)
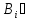 Г.
В случае 1), ввиду
Г.
В случае 1), ввиду
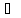 A
A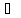 A
(пример 1), имеем
A
(пример 1), имеем
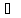 A
A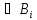 и, следовательно, Г
и, следовательно, Г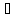 A
A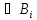 .
В случаях 2) и 3) выводом A
.
В случаях 2) и 3) выводом A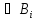 из Г служит последовательность
из Г служит последовательность
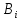 ,
,
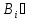 (A
(A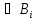 ),
A
),
A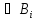 ,
в которой первая формула является
аксиомой или принадлежит Г, вторая
формула есть аксиома 1 и третья получена
из них по правилу отделения.
,
в которой первая формула является
аксиомой или принадлежит Г, вторая
формула есть аксиома 1 и третья получена
из них по правилу отделения.
1.
A![]() (B
(B![]() A)
A)
В
качестве единственного правила
вывода в
ИВ мы принимаем правило modus ponens, или правило
отделения![]() ,по
которому, каковы бы ни были формулы A и B,
из формул A и A
,по
которому, каковы бы ни были формулы A и B,
из формул A и A![]() B
получается формула B.
При i ≤
2 других случаев нет, и база индукции
установлена. При i >
2 возможен еще один случай: 4) Bi получена
из Bj и Bk для
некоторых j, k <i по
правилу отделения, Bk =
(Bj
B
получается формула B.
При i ≤
2 других случаев нет, и база индукции
установлена. При i >
2 возможен еще один случай: 4) Bi получена
из Bj и Bk для
некоторых j, k <i по
правилу отделения, Bk =
(Bj![]() Bi)
и, по предположению индукции, Г
Bi)
и, по предположению индукции, Г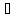 A
A![]() Bj и Г
Bj и Г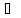 A
A![]() Bk,
т.е. Г
Bk,
т.е. Г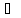 A
A![]() (Bj
(Bj![]() Bi).
В этом случае вывод A
Bi).
В этом случае вывод A![]() Bi из Г строится
так: из Г выводится A
Bi из Г строится
так: из Г выводится A![]() Bj,
берется аксиома 2 в виде
(A
Bj,
берется аксиома 2 в виде
(A![]() Bj)
Bj)![]() ((A
((A![]() (Bj
(Bj![]() Bi))
Bi))![]() (A
(A![]() Bi))
и по правилу отделения
Bi))
и по правилу отделения
2.
(A![]() B)
B)![]() ((A
((A![]() (B
(B![]() C))
C))![]() (A
(A![]() C))
C))
В
качестве единственного правила
вывода в
ИВ мы принимаем правило modus ponens, или правило
отделения![]() ,по
которому, каковы бы ни были формулы A и B,
из формул A и A
,по
которому, каковы бы ни были формулы A и B,
из формул A и A![]() B
получается формула B.
Получается формула (A
B
получается формула B.
Получается формула (A![]() (Bj
(Bj![]() Bi))
Bi))![]() (A
(A![]() Bi),
из Г выводится A
Bi),
из Г выводится A![]() (Bj
(Bj![]() Bi)
и из последних двух формул по правилу
отделения получается требуемая
формула A
Bi)
и из последних двух формул по правилу
отделения получается требуемая
формула A![]() Bi.
Bi.
