Вопросы_по_мат_логике_3_сем_экз_Дьячков / matlog

1) Алгебра высказываний; пропозициональные связки

Для отражения и формализации связок между высказываниями на мат. уровне вводятся операции над высказываниями. Определить каждую операцию – значит приписать истинностное значение результату операции в зависимости от истинностных значений ее аргументов. Для этого удобны истинностные таблицы.

Символы ⌐, &, v, →, ≡ называются пропозициональными (или логическими) связками.

Основные виды пропозициональных связок и их истинностные таблиц см. в след. Вопросе.

Пропозициональная связка - - операция, позволяющая из данных суждений (высказываний) строить новые суждения (высказывания). В зависимости от того, «связывается» ли в новое высказывание одно либо несколько исходных высказываний, принято различать «унарные» и «бинарные» разновидности пропозициональных связок. К «унарной» разновидности в приведённом списке основных видов пропозициональных связок относя отрицание, остальные же связки трактуются как «бинарные».

Осмысленные формулы, составленные из высказываний (пропозициональных букв), пропозициональных связок, а также скобок называются пропозициональными формами (ПФ).

Если в какой-то части ПФ (пропозициональной формы) пропущены скобки, то операции выполняются в следующем порядке: ⌐, &, v, →, ≡

2) Алгебра высказываний; пропозициональные связки и формы, истинностные таблицы.

Под высказыванием мы понимаем повествовательное предложение, которому мы можем приписать истинностное значение «истина» или «ложь». «Истина» обозначается цифрой 1, а «ложь» цифрой 0. Сами высказывания обозначаются заглавными латинскими буквами.

Для отражения и формализации связок между высказываниями на мат. уровне вводятся операции над высказываниями. Определить каждую операцию – значит приписать истинностное значение результату операции в зависимости от истинностных значений ее аргументов. Для этого удобны истинностные таблицы.

Операции:

1. Отрицание ⌐А (или Ā) высказывания А. («не А»)

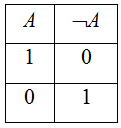
2. Конъюнкция АꓥВ (А&В или А*В) высказываний А и В. («и А, и В»)

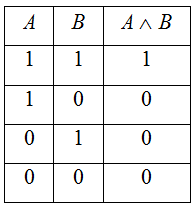
3. Дизъюнкция АꓦВ высказываний А и В. («А или В»)

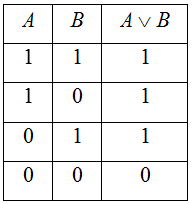
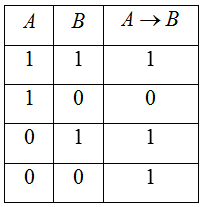
4. Импликация А→И высказываний А и В. («если А, то В»)

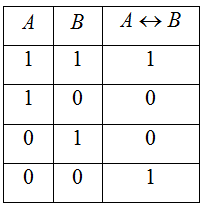
5. Эквивалентность А≡В высказываний А и В. («А тогда и только тогда, когда В»)