Виды асимптот

Определение

Прямая называетсявертикальной асимптотой графика функции , если хотя бы одно из предельных значенийилиравноили.

Замечание. Прямая не может быть вертикальной асимптотой, если функция непрерывна в точке. Поэтому вертикальные асимптоты следует искать в точках разрыва функции.

Определение

Прямая называетсягоризонтальной асимптотой графика функции , если хотя бы одно из предельных значенийилиравно.

Замечание. График функции может иметь только правую горизонтальную асимптоту или только левую.

Определение

Прямая называетсянаклонной асимптотой графика функции , если

7. Нахождение наклонных асимптот.

Теорема(условиях существования наклонной асимптоты)

Если для функции существуют пределыи, то функция имеет наклонную асимптотупри.

Замечание

Горизонтальная асимптота является частным случаем наклонной при .

Замечание

Если при нахождении горизонтальной асимптоты получается, что, то функция может иметь наклонную асимптоту.

Замечание

Кривая может пересекать свою асимптоту, причем неоднократно.

7. Монотонность функции. Необходимое и достаточное условие монотонности.

Функция называетсястрого возрастающей на промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции, т.е.

Функция называетсястрого убывающей на промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции, т.е.

Функция строго возрастающая или строго убывающая на промежутке называетсямонотонной на этом промежутке.

Теорема 1.  Для того, чтобы функция y=f(x) была возрастающей на интервале (a,b), необходимо и достаточно, чтобы первая производная функции была неотрицательной всюду на данном интервале:f′(x)≥0∀x∈(a,b). (Необходимое)

Аналогичный критерий действует для случая функции, убывающей на интервале (a,b):f′(x)≤0∀x∈(a,b). (Достаточное)

Теорема 2.  Для того, чтобы дифференцируемая на интервале (a,b) функция была строго возрастающей на этом интервале, необходимо и достаточно, чтобы выполнялись следующие условия:

1. f′(x)≥0∀x∈(a,b);

2. Производная f′(x) тождественно не равна нулю ни в каком промежутке [x1,x2]∈(a,b).

Условие 1 содержится в теореме 1 и является признаком неубывающей функции. Дополнительное условие 2требуется для того, чтобы исключить участки постоянства функции, в которых производная функции f(x)тождественно равна нулю. 

7. Дифференциал длины дуги.

Дифференциал длины дуги 

     В декартовых координатах:

     В полярных координатах:

7. Кривизна кривой. Радиус кривизны. Центр кривизны.

    Определение 1. Абсолютная величина (длина) скорости вращения единичного касательного вектора к кривой в данной ее точке относительно переменной длины дуги называется кривизной кривой в этой точке.     Если Г = {r(t); a < t < b} - гладкая кривая, a s = s(t) - переменная длина ее дуги, отсчитываемая от начала кривой Г, то вектор

= dr/ds

(18.1)

является единичным касательным вектором к кривой Г. Поэтому кривизна кривой в данной ее точке, обозначаемая обычно через k, согласно данному определению задается формулой

k = |d/ds|.

(18.2)

Отсюда в силу соотношения (18.1) следует, что

k = |d2r/ds2|.

(18.3)

Из этой формулы видно, что определение (18.2) имеет смысл тогда, когда функция r(s) является по крайней мере дважды дифференцируемой.      Величина, обратная кривизне, называется радиусом кривизны кривой в данной точке и обозначается через R. Таким образом,

R = 1/k.	(18.4)

 Точка пространства, находящаяся на расстоянии, равном радиусу кривизны от точки кривой в направлении вектора главной нормали, называется центром кривизны кривой в рассматриваемой точке этой кривой.

   Пусть R - радиус кривизны кривой Г в точке M₀. Если - радиус-вектор центра кривизныM, а r, как обычно, есть радиус-вектор данной точки M₀ кривой, то (рис. 98) =r + R,

(18.26)

    Найдем выражение вектора через производные векторной функцииr по произвольному параметру t.      Подставив в формулу (18.26) выражение для d²r/ds²  через производные по  t (см. (18.13)) и выражение для кривизны

получим , а так как(предполагается, что при возрастании параметраt длина дуги s = s(t) также возрастает), то

(18.27)

где s' = |r'| = (x' ² + y' ² + z' ²)^1/2, поэтому

(18.28)

    Формулу (18.27) можно рассматривать как векторное представление некоторой кривой, точками носителя которой являются центры кривизны данной кривой. Эта кривая называется эволютой данной кривой.

7. Векторные функции скалярного аргумента. Основные определения. Предел и непрерывность.      Определение 

     На множестве U задана вектор-функция, если с каждой его точкой M сопоставлен вектор . ЕслиU - множество точек на прямой и на ней введена декартова координата t, то вектор-функция на U является вектор-функцией одного скалярного аргумента ; еслиU - множество точек на плоскости и на ней введена декартова система координат Ouv, то имеем вектор-функцию двух скалярных аргументов.     Предел вектор-функции 

     - предел в точке, если

Запись: 

     Если 

     Непрерывность вектор-функции 

     непрерывна в точке , еслиВектор-функция, непрерывная в каждой точке множестваU, называется непрерывной на множестве U.

7. Производная векторной функции скалярного аргумента. Геометрический и механический смысл.

 Производной вектор-функции по скалярному аргументуt называют предел отношения приращения вектор-функции к приращению Dt скалярного аргумента t, т. е.

 (5)

и обозначают символом или.

Таким образом, по определению

 . (6)

4. Производная вектор-функции является новой вектор-функцией и называетсяпроизводной первого порядка. Производная от производной называетсяпроизводной второго порядка и обозначается или, т. е.

 . (7)

Аналогично определяются производные вектор-функций более высоких порядков. Производные вектор-функций порядка старше первого называются производными высших порядков.

Механический смысл

7. Определение функции нескольких переменных. Геометрический смысл функции 2-х переменных. Линии и поверхности уровня. Предел функции нескольких переменных.

Функцией двух переменных называется закон, по которому каждой паре значений независимых переменных (аргументов) изобласти определения соответствует значение зависимой переменной (функции).

Данную функцию обозначают следующим образом:

 либо , или же другой стандартной буквой:

Поскольку упорядоченная пара значений «икс» и «игрек» определяет точку на плоскости, то функцию также записывают через , где– точка плоскостис координатами. Такое обозначение широко используется в некоторых практических заданиях.

Геометрический смысл функции двух переменных очень прост. Если функции одной переменной соответствует определённая линия на плоскости (например,– всем знакомая школьная парабола), то график функции двух переменныхрасполагается в трёхмерном пространстве. На практике чаще всего приходится иметь дело споверхностью, но иногда график функции может представлять собой, например, пространственную прямую (ые) либо даже единственную точку. С элементарным примером поверхности мы хорошо знакомы ещё из курса аналитической геометрии – это плоскость . Предполагая что , уравнение легко переписать в функциональном виде:

Определение: линией уровня функции называется линияна плоскости, в каждой точке которой функция сохраняет постоянное значение:.

7. Непрерывность функции нескольких переменных. Формулировка основных свойств непрерывной функции. Точки, линии, поверхности разрывов.

8. Частные производные 1-го и высших порядков. Теорема о порядке дифференцирования.

Рассмотрим функцию двух переменных n=2, . Предположим, что функция имеетчастные производные

,                       ,

которые являются функциями двух переменных. Их называют частными производными первого порядка. Предположим, что они дифференцируемы.

Определение 1. Частные производные от частных производных первого порядка называются частными производными второго порядка.

 = ,=.

 = ,=.

 

Две последние называют смешанными производными.

Если полученные функции являются дифференцируемыми, то частные производные от них называются частными производными третьего порядка. Например:

.

 

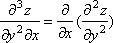Определение 2. Частной производной n-го порядка называется частная производная от частной производной (n-1)-го порядка. Частных производных n-го порядка от функции двух переменных 2ⁿ штук.

Частная производная порядка р функции имеет вид

, где .

Теорема. Если частные производные первого порядка некоторой функции непрерывно дифференцируемы, то результаты смешанного дифференцирования равны.

.

7. Дифференцирование сложных функций нескольких переменных.