Точка разрыва первого рода

Определение

Если в точке существуют конечные пределыи, такие, что, то точканазываетсяточкой разрыва первого рода.

Точка разрыва второго рода

Определение

Если хотя б один из пределов илине существует или равен бесконечности, то точканазываетсяточкой разрыва второго рода.

7. Свойства функций непрерывных на отрезке (теоремы Вейерштрасса и Больцано-Коши).

Свойства функций непрерывных на отрезке:

1. Теорема Вейерштрасса. Если функция непрерывна на отрезке, то она достигает на этом отрезке свои наибольшее и наименьшее значения.

2. Непрерывная на отрезке 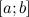функция является ограниченной на этом отрезке.

3. Теорема Больцано-Коши. Если функция является непрерывной на отрезкеи принимает на концах этого отрезка неравные между собой значения, то есть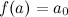,, то на этом отрезке функция принимает и все промежуточные значения междуи.

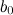4. Если функция , которая непрерывна на некотором отрезке, принимает на концах отрезка значения разных знаков, то существует такая точкатакая, что.

Вторая теорема Вейерштрасса

  Непрерывная на отрезке [a, b] функция ограничена и достигает на этом отрезке своих наибольшего и наименьшего значения (своей верхней и своей нижней грани).

Теорема о промежуточных значениях (Больцано-Коши)

Пусть функция f непрерывна на отрезке [ a,b ], причем f(a) не равно f(b).

Тогда для любого числа C, заключенного между f(a) и f(b) найдется точка γ∈(a,b), что f(γ) = C.

Следствие 1.

Если функция непрерывна на отрезке и на его концах принимает значения разных знаков, то на этом отрезке есть хотя бы одна точка, в которой функция обращается в нуль.

7. Производная функции одной переменной. Основные определения. Геометрический и механический смысл.

Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке).

Определение производной функции через предел

Пусть в некоторой окрестности точки определена функция

Производной функции в точкеназывается предел, если он существует,

Геометрический и физический смысл производной

Тангенс.

Если функция имеет конечную производную в точкето в окрестностиеё можно приблизить линейной функцией

Функция называется касательной кв точкеЧислоявляется угловым коэффициентом или тангенсом угла наклона касательной прямой.

Скорость изменения функции

Пусть — закон прямолинейного движения. Тогдавыражает мгновенную скорость движения в момент времениВторая производнаявыражает мгновенное ускорение в момент времениВообще производная функциив точкевыражает скорость изменения функции в точке, то есть скорость протекания процесса, описанного зависимостью

7. Дифференциал функции одной переменной. Геометрический смысл. Необходимое и достаточное условие существования дифференциала. Инвариантность формы дифференциала.

Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)):

dy=ƒ'(х)•∆х.                                             (24.1)

Дифференциал dу называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции у=х.

Так как у'=х'=1, то, согласно формуле (24.1), имеем dy=dx=∆x, т. е. дифференциал независимой переменной равен приращению этой переменной: dх=∆х.

Поэтому формулу (24.1) можно записать так:

dy=ƒ'(х)dх,    

Геометрический смысл дифференциала:

Проведем к графику функции в точкукасательнуюи рассмотрим

ординату этой касательной для точки . На рисунке,. Из прямоугольного треугольникаимеем:, т.е.. Но, согласно геометрическому смыслу производной,. Поэтомуили. Это означает, что дифференциал функциивравен приращению ординаты касательной к графику функции в этой точке, когдаполучает приращение.

Необходимое и достаточное условие существования дифференциала

Для того, чтобы функция f(x) была дифференцируема в точке x₀ необходимо и достаточно, чтобы у нее существовала производная в этой точке.

При этом

Δy = f(x0+Δx)-f(x0) = f '(x0)Δx+α(Δx)Δx,

где α(Δx) - бесконечно малая функция, при Δx→0.