Предел функции на бесконечности. Бесконечно большая функция

Рассмотрим функцию , заданную на.

Определение

Число называетсяпределом функции на бесконечности или при , если для любогосуществует числотакое, что для всехиз того, что, выполняется неравенство.

4. Бесконечно малые функции, их свойства. Связь с бесконечно большими.

Определение

Функция называетсябесконечно малой функцией (б.м.ф.) при (или в точке), если

Пример

Функция является бесконечно малой (б.м) функцией при.

Основные свойства бесконечно малых функций

1°   Сумма конечного числа б.м функций является функцией б.м.

2°   Произведение б.м функции на ограниченную есть функция б.м.

3°   Произведение двух б.м функций есть функция б.м.

4°   Произведение б.м функции на константу является б.м функцией.

5°   Частное от деления б.м функции на функцию, предел которой не равен нулю, есть функция б.м.

6°   Функция , обратная к б.м функции, есть функция бесконечно большая. Верно и обратное.(связь б.м. и б.б.)

5.Бесконечно большие функции. Связь с бесконечно малыми.

Определение

Функция называетсябесконечно большой в точке , если для любогосуществует такое, что для любого, удовлетворяющего неравенству, выполняется неравенство:. В этом случае пишут:

Пример

Бесконечно большой функцией в точке 0 является функция 

Определение

Функция называетсябесконечно большой при , если для любогосуществует такое числотакое, что для всехиз области определения функции, которые удовлетворяют неравенству, выполняется неравенство:

6.Предел функции и его свойства.

Определение предела функции по Коши

Определение

Число называетсяпределом функции в точке , если длятакое, что дляиз того, чтоследует, что:илипри.

Свойства пределов функции

1°   Предел суммы/разности двух функций равен сумме/разности их пределов:

2°   Предел произведения двух функций равен произведению их пределов:

3°   Предел частного двух функций равен частному их пределов, при условии, что предел знаменателя не равен нулю:

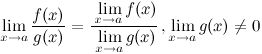
4°   Константу можно выносить за знак предела:

5°   Предел степени с натуральным показателем равен степени предела:

7. Теорема о связи функции, ее предела и бесконечно малой функции.

Теорема

Пусть -предел функции в точке:. Тогда заданную функцию можно представить в виде, где- б.м функция. Верно и обратное утверждение.

Теорема о функции, её пределе и бесконечно малой функции.

Теорема 1 (о связи предела с бесконечно малой функцией). Для того, чтобы существовал

 

lim x→x0   f(x) = A,

 

необходимо и достаточно, чтобы функцию f(x) можно было представить в виде

 

f(x) = A + α(x),

 

где α(x) — бесконечно малая функция при x → x₀.

7. Теоремы о эквивалентных бесконечно малых функциях

Определение

Б.м. функции иназываютсяэквивалентными или равносильными б.м. одного порядка при , если

Обозначают: при.

Теорема

Предел отношения двух б.м. функций иприравен пределу отношения эквивалентных им б.м. функцийипри, то есть верны предельные равенства:

Теорема

Разность двух эквивалентных б.м. функций есть б.м. функция более высокого порядка, чем каждая из них.

Верно и обратное утверждение.

Теорема

Сумма конечного числа б.м. функций разных порядков эквивалентна слагаемому низшего порядка.

7. Эквивалентные бесконечно малые и их использование при вычислении пределов.

Быстрым способом нахождения пределов функций имеющих особенности выда ноль на ноль является применение эквивалентных бесконечно малых функций. Они крайне необходимы если нужно находить границы без применения правила Лопиталя.

7. Сравнение бесконечно малых. Таблица эквивалентных б.м..