
- •1. Функции. Основные определения и свойства. Способы задания. Классификация.
- •Способы задания функции
- •1)Аналитический способ
- •2)Табличный способ
- •3)Графический способ
- •2. Предел функции точке. Односторонние пределы.
- •Предел функции на бесконечности. Бесконечно большая функция
- •Сравнение бесконечно малых Допустим, у нас есть бесконечно малые при одном и том же величиныи(либо, что не важно для определения, бесконечно малые последовательности).
- •Раскрытие неопределенностей
- •Непрерывность функции на промежутке
- •Точка разрыва первого рода
- •Точка разрыва второго рода
- •Свойства функций непрерывных на отрезке:
- •Инвариантность формы дифференциала
- •Геометрический смысл дифференциала
- •Формула
- •Доказательство
- •Доказательство Отношение бесконечно малых
- •Отношение бесконечно больших Докажем теорему для неопределённостей вида .
- •Производные высших порядков
- •Формула Тейлора
- •Понятие экстремума функции
- •Необходимое условие экстремума
- •Понятие экстремума функции
- •Первое достаточное условие экстремума
- •Виды асимптот
- •Производная степенно-показательной функции
1. Функции. Основные определения и свойства. Способы задания. Классификация.
Вещественные
функции вещественного аргумента делят
на два класса: элементарные и не
элементарные.
ОПРЕДЕЛЕНИЕ. Элементарной
функцией называется функция, которая
может быть задана одной формулой
![]() ,
где
,
где![]() –
выражение, составленное из основных
элементарных функций и действительных
чисел с помощью конечного числа операций
сложения, вычитания, умножения, деления
и взятия функции от функции.Основными
элементарными функциями называются
следующие функции:
–
выражение, составленное из основных
элементарных функций и действительных
чисел с помощью конечного числа операций
сложения, вычитания, умножения, деления
и взятия функции от функции.Основными
элементарными функциями называются
следующие функции:
степенная функция
 ,
где
,
где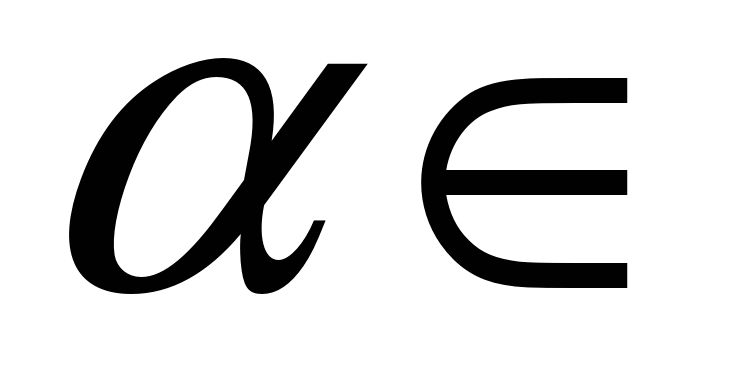 R;
R;показательная функция
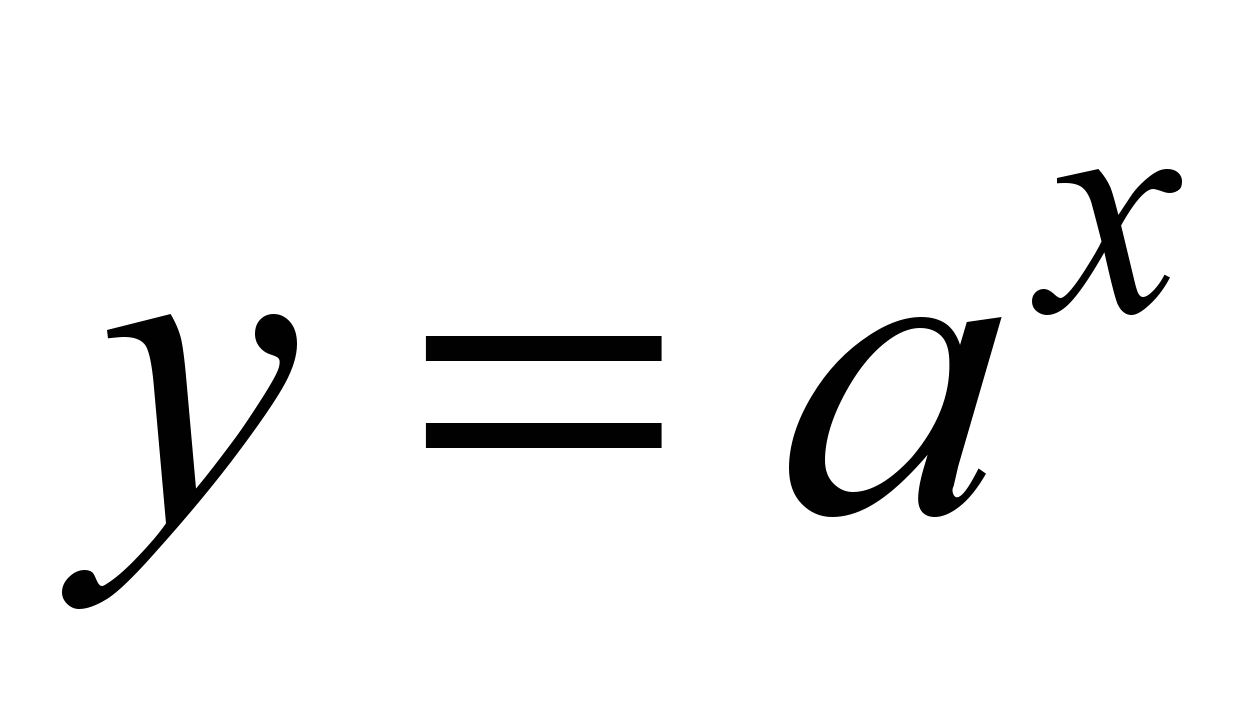 ,
где
,
где и
и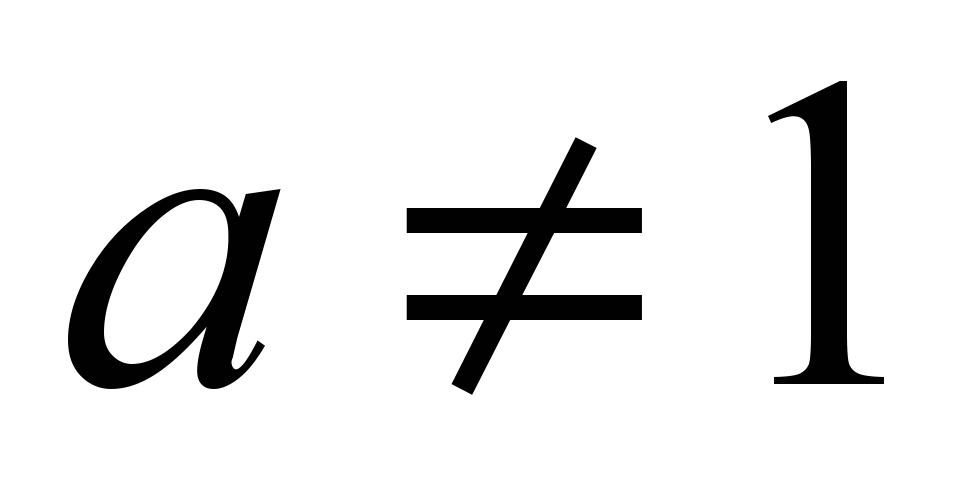 ;
;логарифмическая функция
 ,
где
,
где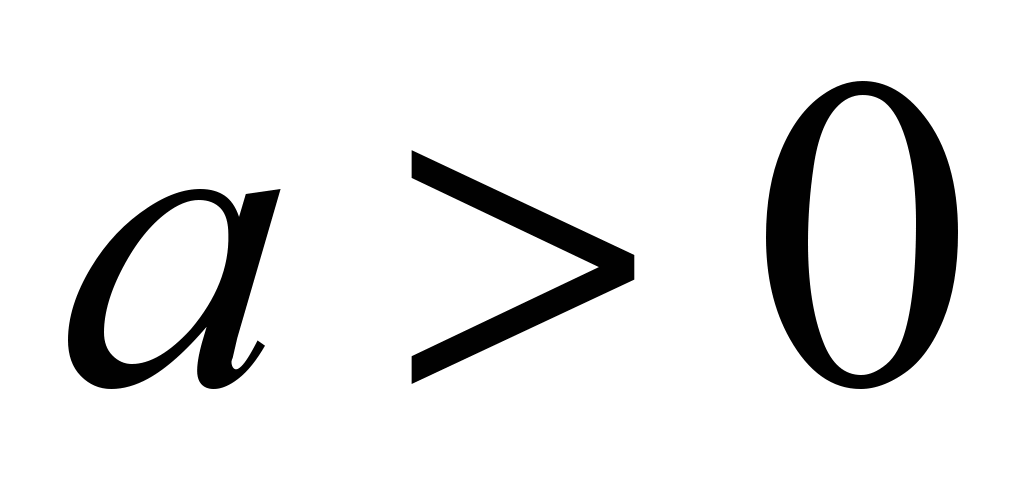 и
и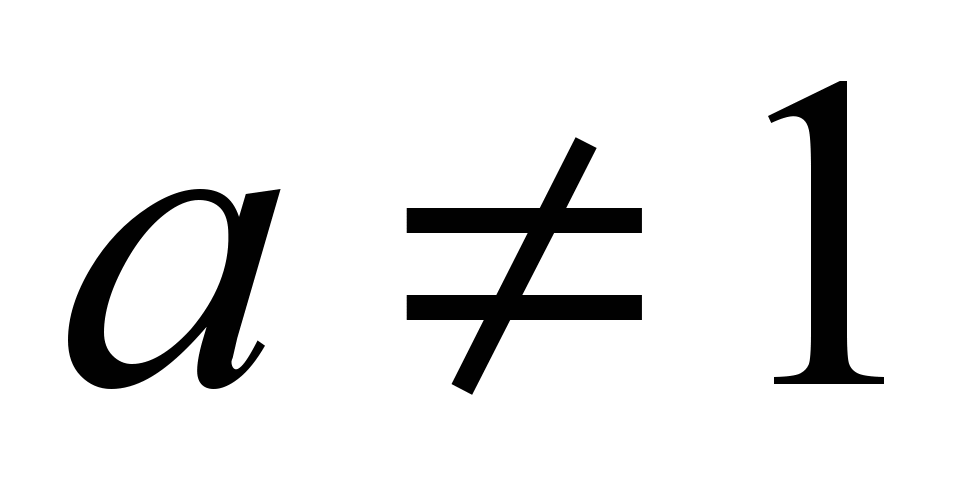 ;
;тригонометрические функции
 ,
,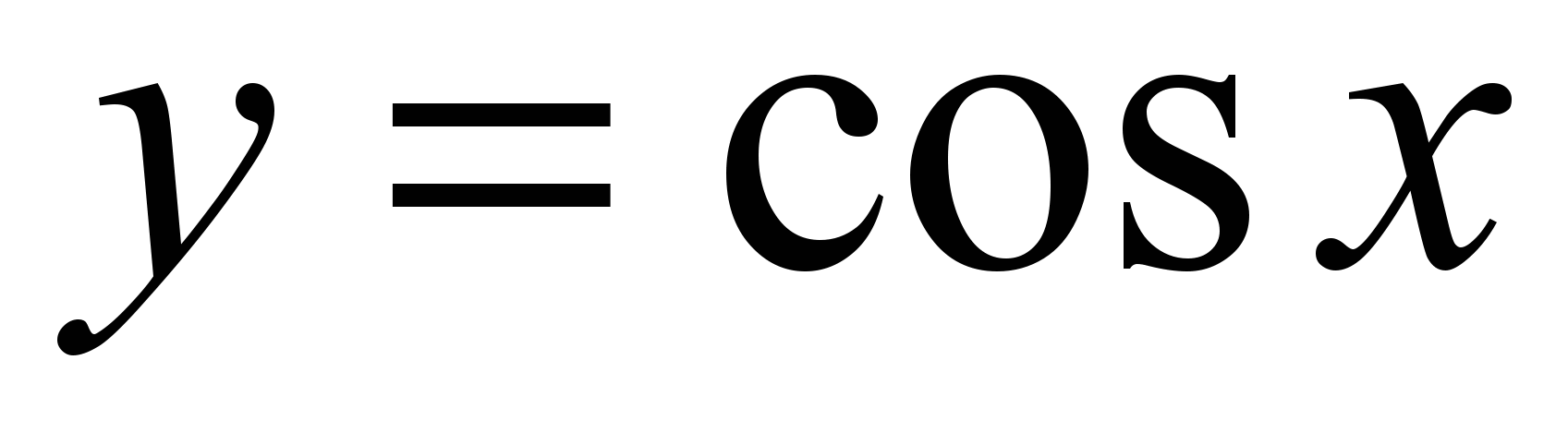 ,
, ,
,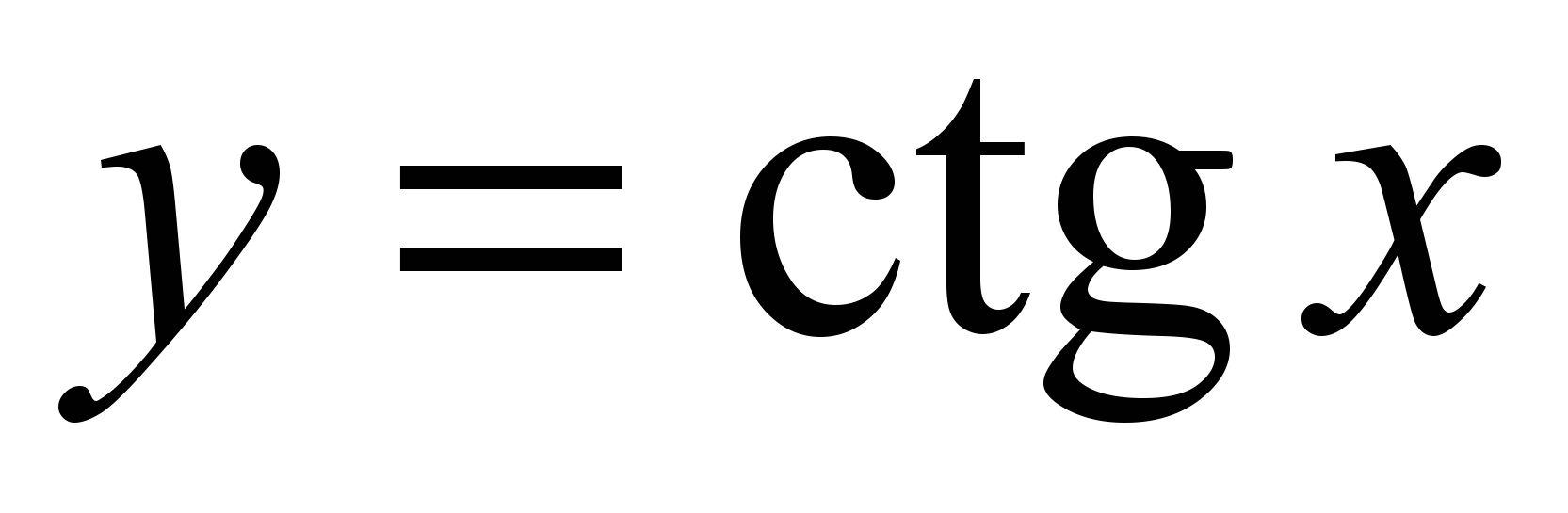 ;
;обратные тригонометрические функции
 ,
,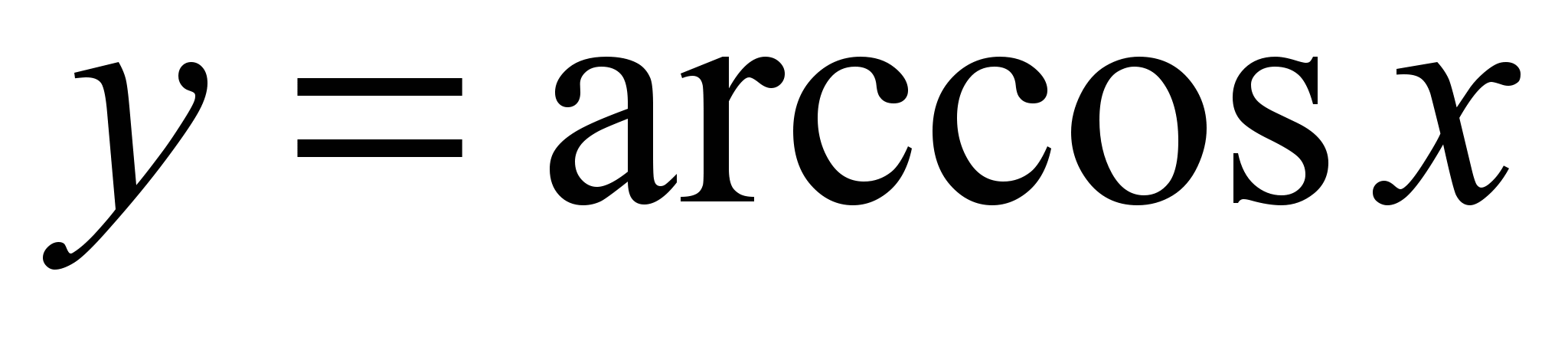 ,
, ,
,
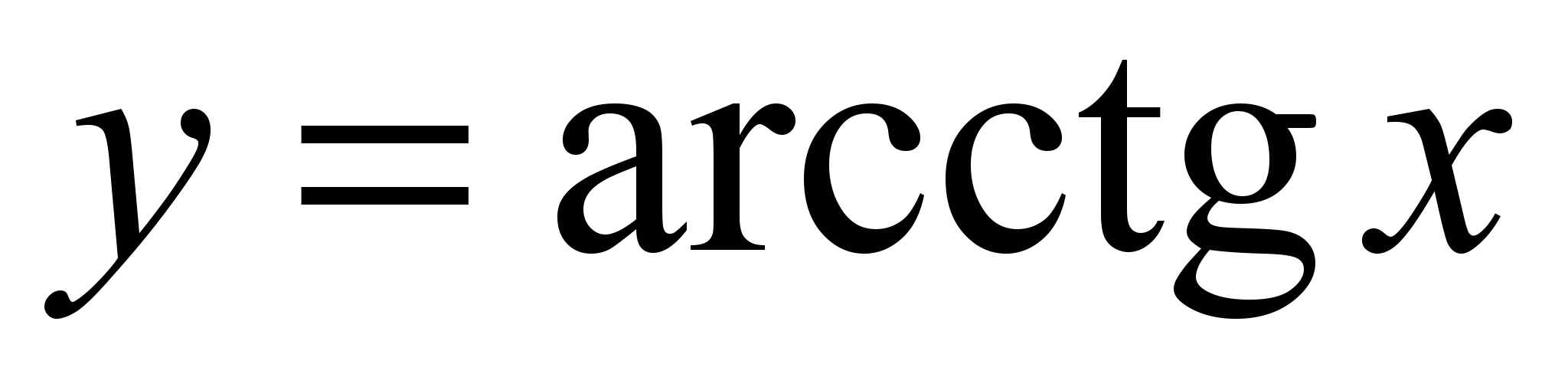 .
.
Областью
определения функции
![]() (выраженияf(x)
) называют множество всех значений x
, для которых функция (выражение) имеет
смысл.
(выраженияf(x)
) называют множество всех значений x
, для которых функция (выражение) имеет
смысл.
Область
определения функции
![]() обозначается
как
обозначается
как![]() или
или![]() .
.
Способы задания функции
1)Аналитический способ
Закон, устанавливающий связь между аргументом и функцией, задается посредством формул.
2)Табличный способ
Функцию можно задать, перечислив все её возможные аргументы и значения для них.
3)Графический способ
Функцию можно задать графически, отобразив множество точек её графика на плоскости.
|
|
Обратная функция Обратная функция, функция, обращающая зависимость, выражаемую данной функцией. Так, еслиу = f (x) — данная функция, то переменная х, рассматриваемая как функция переменной у, х = j (y), является обратной по отношению к данной функции у = f (x). Например, О. ф. для у = ax + b (а¹0) является х = (у—b)/a.
|
|
|
Сложная функция Сложная функция, функция от функции. Если величина y является функцией от u, то есть у = f (u), а u, в свою очередь, функцией от х, то есть u = j(х), то у является С. ф. от х, то есть y = f [(x)], определённой для тех значений х, для которых значения j(х) входят в множество определения функции f (u). В таком случае говорят, что у является С. ф. независимого аргумента х, а u — промежуточным аргументом. Например, если у = u2, u = sinx, то у = sin2х для всех значений х. |
2. Предел функции точке. Односторонние пределы.
Предел функции в точке
Пусть
задано некоторое числовое множество ![]() и
каждому
и
каждому![]() поставлено
в соответствие число
поставлено
в соответствие число![]() ,
тогда говорят, что на множестве
,
тогда говорят, что на множестве![]() задана
функция
задана
функция![]() ,
,![]() .
.
Определение предела функции по Коши
Определение
Число ![]() называетсяпределом
функции
называетсяпределом
функции ![]() в
точке
в
точке ![]() ,
если для
,
если для![]()
![]() такое,
что для
такое,
что для![]() из
того, что
из
того, что![]() следует,
что
следует,
что![]() :
:![]() или
или![]() при
при![]() .
.
Односторонние пределы
Определение
Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами.
Левый и правый пределы функции
Определение
Число ![]() называетсяправым
пределом функции
называетсяправым
пределом функции ![]() в
точке
в
точке ![]() ,
если для
,
если для![]()
![]() такое,
что для любого
такое,
что для любого![]() и
и![]() ,
выполняется неравенство
,
выполняется неравенство![]() (рис.
1). Правый предел обозначается
(рис.
1). Правый предел обозначается![]()
Число ![]() называетсялевым
пределом функции
называетсялевым
пределом функции ![]() в
точке
в
точке ![]() ,
если для
,
если для![]()
![]() такое,
что для любого
такое,
что для любого![]() и
и![]() ,
выполняется неравенство
,
выполняется неравенство![]() (рис.
2). Левый предел обозначается
(рис.
2). Левый предел обозначается![]()
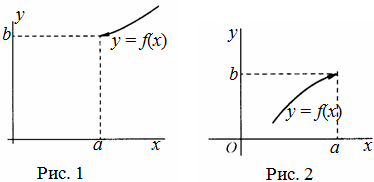
Левый и правый пределы функции называются односторонними пределами.
Теорема
Если
существуют ![]() и
и![]() ,
причем
,
причем![]() ,
то существует и
,
то существует и![]() .
Обратное утверждение также верно.
.
Обратное утверждение также верно.
В
случае, если ![]() ,
то предел
,
то предел![]() не
существует.
не
существует.
3. Предел функции в точке. Предел на бесконечности. Первая часть в предыдущем вопросе.
