Мет_указ_лаб_ТУ
.pdfМинистерство образования Российской Федерации
___________________________________________
Санкт-Петербургский государственный электротехнический университет ”ЛЭТИ”
Исследование линейных систем в среде MATLAB/SIMULINK
Методические указания к лабораторным работам по дисциплине «Теория управления»
Санкт-Петербург Издательство СПбГЭТУ "ЛЭТИ"
2004
УДК 519.71(075.9)
Исследование линейных систем в среде MATLAB/SIMULINK: Методические указания к лабораторным работам по дисциплине “Теория управления” / Сост.: А. А. Бурмистров, В. Б. Второв, И. А. Приходько, О. Э. Якупов. СПб.: Издательство СПбГЭТУ "ЛЭТИ", 2004. 24 с.
Содержат программы и методики выполнения лабораторных работ по анализу математических моделей систем автоматического управления на ЭВМ.
Предназначены для студентов направлений 550200, 551300, 652300, 651900, 652000, специальности 210500 и других специальностей факультета электротехники и автоматики.
Утверждено редакционно-издательским советом университета
в качестве методических указаний
© СПбГЭТУ "ЛЭТИ", 2004
2
Предисловие
Настоящие методические указания предназначены студентам, выполняющим лабораторный практикум по дисциплине "Теория управления" учебных планов подготовки бакалавров по направлениям 550200 "Автоматизация и управление", 551300 "Электротехника, электромеханика, электротехнологии" и инженеров по специальности 210500 "Системы управления летательными аппаратами" и ряду других специальностей факультета электротехники и автоматики СПбГЭТУ "ЛЭТИ".
Материал лабораторных работ охватывает широкий круг типовых задач анализа систем автоматического управления во временнόй, комплексной и частотных областях. Несколько последних работ направлены на углубление понимания студентами некоторых методов синтеза автоматических систем.
Предполагается, что все работы выполняются на персональном компьютере с использованием системы моделирования MATLAB / SIMULINK или другого пакета, позволяющего осуществлять математическое моделирование динамических систем.
Описание каждой лабораторной работы начинается с краткого изложения основных сведений, необходимых для ее выполнения, и заканчивается контрольными вопросами для самопроверки. В зависимости от технических возможностей лабораторной базы и простой целесообразности иллюстративный материал, включаемый студентами в свои отчеты, может содержать как твердые копии экрана, так и выполненные от руки эскизы.
Лабораторная работа №1
ИССЛЕДОВАНИЕ ДИНАМИЧЕСКИХ СВОЙСТВ ТИПОВЫХ ЗВЕНЬЕВ САУ ВО ВРЕМЕННОЙ И ЧАСТОТНОЙ ОБЛАСТЯХ
Цель работы – анализ переходных и частотных характеристик важнейших типовых звеньев систем автоматического управления.
1.1. Основные сведения
Переходная характеристика (ПХ) динамического звена (или системы) –
это |
его реакция y(t) на единичное ступенчатое входное воздействие |
u(t) |
1(t) при нулевых начальных условиях (ННУ). Для ПХ обычно исполь- |
зуют специальное обозначение h(t) . Передаточной функцией (ПФ) звена называют отношение изображения по Лапласу выходной и входной переменных этого звена при ННУ: W (p) Y (p) /U (p) .
3
Частотная передаточная функция (ЧПФ) W ( j ) получается из ПФ под-
становкой p j . Годограф функции W ( j |
)при изменении аргумента |
от 0 |
|||||||
до |
называется |
амплитудно-фазовой частотной |
характеристикой |
||||||
(АФХ). Если ЧПФ |
представлена в |
показательной |
форме W( j |
) |
|||||
A ( |
)e j ( ), то функции A( ) |
|
W ( j ) |
|
, |
( ) arg W ( j |
) называются, со- |
||
|
|
||||||||
ответственно, амплитудной (АЧХ) и фазовой (ФЧХ) частотными характе-
ристиками. Они характеризуют поведение устойчивого звена (системы) в установившемся режиме при гармоническом входном воздействии и могут быть определены экспериментально. Для этого на вход исследуемого звена необходимо подавать гармоническое воздействие постоянной амплитуды и различной частоты. Тогда установившаяся реакция звена на это воздействие будет также гармонической функцией той же частоты, но, вообще говоря, другой амплитуды и с фазовым сдвигом относительно входной гармоники. Отношение амплитуд выходной и входной гармоник на каждой заданной частоте равно значению АЧХ, а относительный фазовый сдвиг этих функций – значению ФЧХ на указанной частоте.
Функция L( ) 20 lg A( ) называется логарифмической амплитудной частотной характеристикой (ЛАХ) и графически изображается как функция частоты , рад/c, откладываемой по оси абсцисс в логарифмическом масштабе, т. е. фактически как функция безразмерной переменной lg , откладываемой в равномерном масштабе. Значения L( ) измеряются в децибелах (дБ) и откладываются по оси ординат в равномерном масштабе. ФЧХ, изображаемая как функция частоты, откладываемой в логарифмиче-
ском масштабе, называется логарифмической фазовой частотной харак-
теристикой (ЛФХ). Ее значения измеряются в градусах или радианах. ЛАХ и ЛФХ называются логарифмическими частотными характеристиками
(ЛЧХ).
1.2.Программа работы
1.Задать интегрирующее звено с передаточной функцией W (p) 1/Tp ,
взяв значение T из табл. 1.1 (номер варианта задает преподаватель).
2. Выполнить анализ характеристик звена и ответить на приведенные вопросы.
а) Чему равно значение ПХ h(t) при t T ?
б) Что представляют собой графики ЛАХ и ЛФХ ? в) На какой частоте ЛАХ пересекает ось абсцисс ?
г) Как изменятся ПХ и ЛАХ при увеличении значения T вдвое ?
4
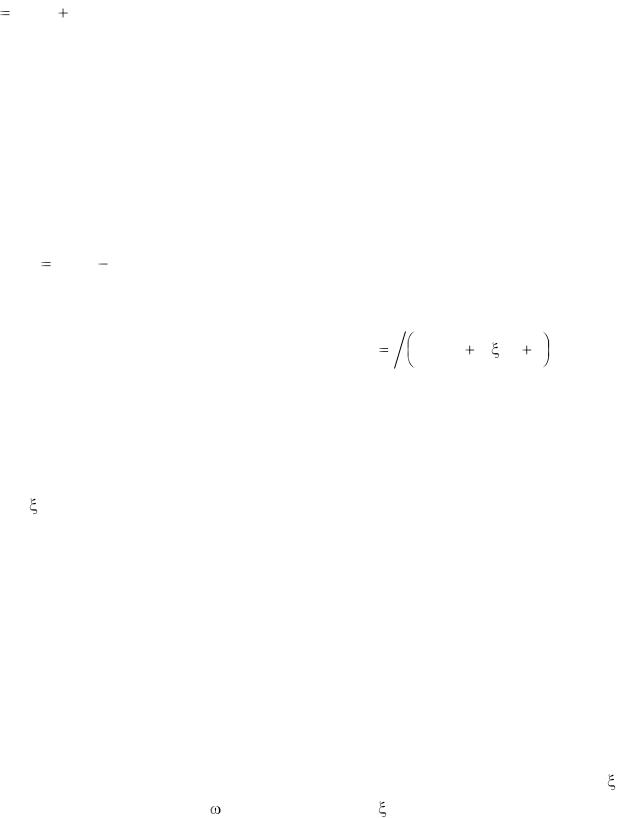
3. Задать апериодическое звено первого порядка с ПФ W (p) 
1/ (Tp 1) , взяв то же значение T , что и в п. 1.
4. По результатам анализа ответить на приведенные вопросы. а) Чему равно значение h(3T ) ?
б) Каков полюс ПФ ?
в) Каковы значения ЛАХ и ЛФХ на частотах 1/ T , 0.1/ T и 10 / T ?
г) Как изменятся значения ПХ и ЛЧХ при уменьшении значения T в 2 раза ? Что при этом произойдет с АФХ ?
д) Как изменятся значения ПХ и ЛЧХ при увеличении коэффициента пе-
редачи в 2 раза ? |
|
|
|
|
|
|
|
|
|
|
||||
5. |
Задать неустойчивое апериодическое звено первого порядка с ПФ |
|||||||||||||
W (p) |
1/ (Tp |
1) , назначив значение T в соответствии с п. 1. |
|
|
||||||||||
6. |
На основании анализа ПХ, ЛАХ, ЛФХ, АФХ, полюса ПФ дать характе- |
|||||||||||||
ристику различий в свойствах звеньев, заданных в пп. 3 и 5. |
|
|
||||||||||||
7. |
Задать колебательное звено с ПФ W (p) 1 |
T 2p2 |
2 Tp |
1 с пара- |
||||||||||
метрами из табл. 1.1. |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 1.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Параметр |
|
|
|
|
|
|
Вариант |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
1 |
|
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
9 |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T , с |
|
0.1 |
|
0.2 |
0.25 |
0.4 |
0.5 |
0.8 |
1.0 |
1.25 |
|
1.6 |
2.0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.4 |
|
0.3 |
0.25 |
0.2 |
0.1 |
0.08 |
0.06 |
0.05 |
|
0.04 |
0.03 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. Выполнить анализ характеристик звена и ответить на приведенные вопросы.
а) Как влияет на показатель качества ПХ (максимальное значение, длительность переходного процесса, период колебаний) уменьшение коэффициента затухания 
в 5 раз по сравнению с заданным?
б) Как повлияет на эти же показатели уменьшение постоянной времени T в 2 раза ?
в) Как меняется картина расположения полюсов передаточной функции при изменении 
и T ?
г) Что происходит с высотой резонансного пика ЛАХ при уменьшении
и с резонансной частотой |
р |
при уменьшении ? |
|
|
9. Увеличить значение 
до произвольного значения, большего или равного единице, превратив тем самым звено в апериодическое звено вто-
5
рого порядка. Описать изменения, произошедшие с ПХ и с расположением полюсов на комплексной плоскости.
10. Определить путем имитации реального эксперимента значения АЧХ (ЛЧХ) и ФЧХ (ЛФХ) апериодического звена (значение T взять из табл.1.1) при трех значениях частоты : 1/T, 0.1/T, 10 /T . Рекомендуется воспользоваться следующей последовательностью действий:
на вход исследуемого звена подать гармонический сигнал единичной амплитуды и заданной частоты;
определить амплитуду выходного сигнала Ym и его временной сдвиг t относительно входного; указанные измерения следует производить по прошествии интервала времени не менее 3T , когда наблюдаемый на выходе звена процесс можно считать установившимся; удобно совместить в
одном окне входной и выходной процессы с помощью мультиплексора;
определить значения АЧХ и ФЧХ как A( ) Ym и ( ) |
t , а также |
вычислить L ( ); |
|
полученные для каждого значения частоты данные занести в таблицу. 11. Описанным в предыдущем пункте способом определить значения АЧХ (ЛЧХ) и ФЧХ (ЛФХ) колебательного звена с параметрами, взятыми из
табл. 1.1, при указанных значениях частоты.
1.3.Содержание отчета
1.Ответы на вопросы, содержащиеся в программе работы.
2.Результаты экспериментального определения АЧХ и ФЧХ (и, соответственно, ЛЧХ и ЛФХ) апериодического и/или колебательного звеньев. Изобразить теоретические графики асимптотических ЛАХ рассматриваемых звеньев и нанести на них точки, определенные экспериментально, а также
в4, в). Прокомментировать результаты.
Контрольные вопросы
1.Дайте определения передаточной функции, частотной передаточной функции, АЧХ, ФЧХ, ЛАХ, ЛФХ звена (системы).
2.Каков "физический смысл" АЧХ и ФЧХ (с точки зрения реакции на гармоническое воздействие)?
3.Зависит ли точность экспериментального определения АЧХ и ФЧХ от интервала наблюдения?
4.Выведите аналитические выражения для переходных характеристик интегрирующего и апериодического звеньев.
6
5.Каков "физический смысл" постоянной времени интегрирующего зве-
на?
6.Укажите максимальное число способов определения постоянной времени апериодического звена по графику его переходной характеристики.
7.Как связаны полюсы ПФ колебательного звена с поведением огибающей его переходной характеристики и частотой колебаний?
8.Выведите аналитическую зависимость между значением ЛАХ колеба-
тельного звена на частоте 1/ T и коэффициентом затухания .
Лабораторная работа № 2
ВЛИЯНИЕ ПАРАМЕТРОВ НА КАЧЕСТВО АВТОМАТИЧЕСКИХ СИСТЕМ
Цель работы – изучение влияния изменения параметров системы на показатели качества и на характер протекающих в системе процессов.
2.1. Основные сведения
Важнейшими показателями качества (ПК) переходной характеристики (ПХ) h(t) , или прямыми показателями качества системы являются:
время регулирования t р – время, по истечении которого ПХ не выходит из области допустимых (обычно пятипроцентных) отклонений от уста-
новившегося значения (УЗ) h( ) : |
h(t) h( ) |
, t tр , где |
0.05 h( ) ; |
||||
время нарастания |
tн – время первого достижения УЗ; |
|
|||||
перерегулирование |
– превышение максимума ПХ над УЗ в про- |
||||||
центах от УЗ: |
hmax |
h( ) |
100 . |
|
|
|
|
h( |
) |
|
|
|
|
||
|
|
|
|
|
|
||
Среди косвенных ПК систем автоматического управления широко употребляются частотные и корневые.
Некоторые частотные ПК:
частота среза с – частота, при которой ЛАХ разомкнутой системы пересекает ось абсцисс: L( с ) 0 ; служит мерой быстродействия системы; 
запас устойчивости по фазе 
– превышение ЛФХ разомкнутой сис-
темы на частоте среза над уровнем –180 (в устойчивой системе): |
180 + |
+ ( с ) ; с уменьшением 
переходные процессы становятся более колебательными;
7
полоса пропускания |
п – частота, при которой значение АЧХ замкну- |
||
|
|
|
|
той системы в 2 раз меньше ее значения на нулевой частоте: A з ( п ) |
|||
0.707 A з (0) или L з ( п ) |
L з (0) 3 дБ ; является мерой быстродействия |
||
системы; |
|
||
показатель колебательности M – отношение максимального значения АЧХ замкнутой системы к начальному значению: M A з max 
A з (0) ; характеризует склонность системы к колебаниям.
Основные корневые ПК:
степень устойчивости 
– расстояние от мнимой оси до ближайшего корня (или пары комплексно-сопряженных корней) характеристического полинома (ХП) замкнутой системы; является мерой быстродействия; если ПФ не имеет нулей, то при увеличении действительной и мнимой частей каждого полюса в k раз длительность переходного процесса сократится также в k раз;
колебательность 
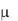– отношение модулей мнимой и вещественной частей ближайшей к мнимой оси пары комплексных корней ХП; чем больше
, тем меньше затухание колебаний за период.
Некоторые способы суждения об устойчивости системы:
для асимптотической устойчивости необходимо и достаточно, чтобы все корни ХП располагались в левой полуплоскости; если один корень находится в начале координат или одна пара корней – на мнимой оси (остальные – в левой полуплоскости), то система находится на границе устойчивости – соответственно, апериодического или колебательного типа);
в асимптотически устойчивой системе все коэффициенты ХП положительны; если хотя бы один из коэффициентов ХП отрицателен, система неустойчива;
согласно критерию Гурвица, для асимптотической устойчивости системы третьего порядка с положительными коэффициентами ХП необходимо и достаточно, чтобы произведение двух средних коэффициентов было больше произведения двух крайних коэффициентов (для колебательной границы устойчивости имеет место равенство этих произведений);
согласно критерию Найквиста, если ПФ разомкнутой системы имеет полюсы только в левой полуплоскости (кроме, возможно, одного нулевого), то для асимптотической устойчивости замкнутой системы необходимо и достаточно, чтобы при изменении частоты от нуля до бесконечности АФХ разомкнутой системы не охватывала точку с координатами (–1, j0), или, что то же самое, чтобы разность между числом положительных (сверху вниз) и
8
отрицательных (снизу вверх) переходов АФХ через луч ( 
, 1] равнялась нулю; в терминах ЛЧХ это соответствует тому, что в диапазоне частот, где ЛАХ разомкнутой системы лежит выше оси, разность между числом положительных (снизу вверх) и отрицательных (сверху вниз) переходов ЛФХ че-
рез горизонтальную прямую с ординатой 180 равняется нулю.
2.2. Программа работы
Работа рассчитана на два занятия: программа первого включает зада-
ния 2.2.1 и 2.2.2, второго – 2.2.3.
2.2.1. Исследование влияния контурного коэффициента усиления системы на ее динамические свойства
1. Задать структурную схему системы третьего порядка, составленную
из последовательно соединенных звеньев с ПФ k p, 1 (T1p 1) |
и 1 (T2 p 1) , |
||||||||||||||||||||
охваченных единичной отрицательной обратной связью. Назначить T1 в со- |
|||||||||||||||||||||
ответствии с нижеприведенными вариантами и задать T2 |
0.1 T1: |
|
|
|
|||||||||||||||||
|
Вариант |
|
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
10 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T1, с |
1.0 |
|
0.1 |
|
2.0 |
|
0.2 |
|
2.5 |
|
0.25 |
|
0.8 |
|
0.5 |
|
0.4 |
|
4.0 |
|
|
2. Для значений k , равных 0.1 T1, 1 T1 и 10 T1 , определить и занести в |
||||||||||||||||||||
таблицу значения t р, t н, , |
|
п, Lз max |
|
20 lg Aз max, корней ХП, |
и |
|
. Опи- |
||||||||||||||
сать изменение характера переходного процесса с увеличением k . |
|
|
|
||||||||||||||||||
|
3. Увеличить k |
до значения 12 T1 . Ответить на вопросы: каким стал пе- |
|||||||||||||||||||
реходный процесс? какие изменения произошли с корнями ХП? |
|
|
|
|
|||||||||||||||||
4. Разомкнуть обратную связь. Для значений k , указанных в пп. 2 и 3, определить и занести в таблицу с и (только для первых трех значений k )
, а также исследовать с позиций критерия Найквиста изменения, происходящие в АФХ и ЛЧХ с ростом k .
2.2.2. Исследование влияния относительной инерционности звеньев системы на ее устойчивость
5. В предыдущей схеме, но с замкнутой обратной связью и со значением k , назначенном в п. 3, уменьшить T1 в 4 раза. Описать изменения, произо-
шедшие в характере переходного процесса и в расположении корней ХП.
6. Задать структурную схему системы, состоящей из трех последовательно соединенных апериодических звеньев с постоянными времени T1,T2
9
и T3 , охваченных единичной отрицательной обратной связью. Одно из звеньев имеет коэффициент передачи k , остальные – единичный.
7. Назначить T1 T2 T3 T , где T – произвольная константа. Подобрать такое значение k кр контурного коэффициента k , при котором система
выйдет на колебательную границу устойчивости, т. е. ПХ примет вид незатухающих колебаний. Определить частоту f , Гц, этих колебаний.
8. Назначить T1 |
T2 |
T3 0.5 T . Снова определить k кр и f , сравнить |
|
их с предыдущими значениями. |
|||
9. Оставив |
k k кр , |
задать новое соотношение постоянных времени: |
|
T1 0.2 T, T2 |
T, T3 |
5T . Охарактеризовать изменения, произошедшие в |
|
свойствах системы. Увеличением k определить новое значение k кр .
10.По результатам исследований в пп. 5–9 ответить на вопрос: какие факторы – абсолютные значения постоянных времени или их соотношения – влияют на устойчивость, характер переходных процессов в системе и на ее критический коэффициент усиления ?
2.2.3.Изучение стандартных полиномов
идиаграммы Вышнеградского
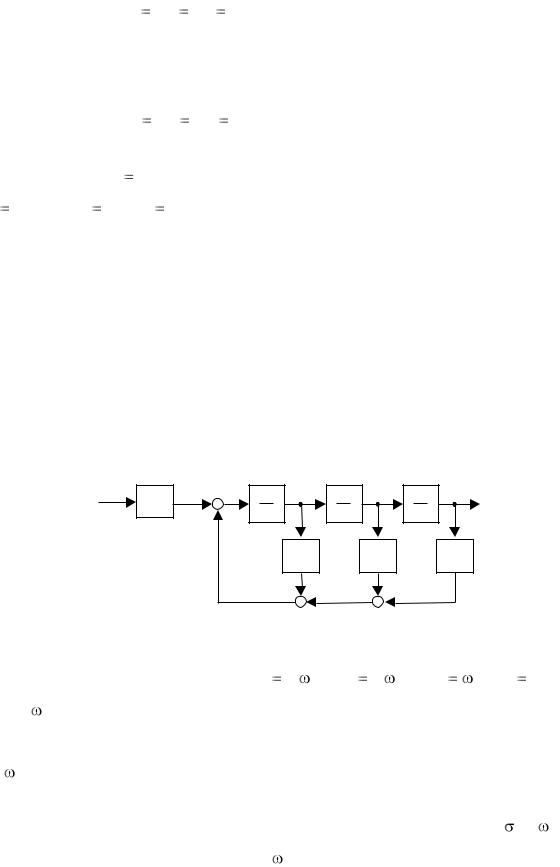
11.Задать структурную схему системы третьего порядка в управляемой канонической форме (рисунок).
u |
|
|
|
y |
b |
|
1 |
1 |
1 |
|
- |
p |
p |
p |
|
|
|
|
|
|
|
a1 |
a2 |
a3 |
|
|
+ |
+ |
|
12. |
Задать систему с единичным коэффициентом передачи и ХП Бат- |
||||||||||||||||||||||||
терворта, для чего назначить a |
|
2 |
0 |
, a |
2 |
2 |
, a |
3 |
, b |
a |
. Зна- |
||||||||||||||
|
|
|
|
|
1 |
|
|
|
2 |
|
0 |
3 |
0 |
|
|
3 |
|
|
|||||||
чение |
0 взять из приведенных ниже: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Вариант |
|
2 |
|
3 |
|
4 |
|
|
5 |
|
|
6 |
|
7 |
|
8 |
|
9 |
|
|
10 |
|
||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 , рад/с |
1 |
10 |
|
2 |
|
5 |
|
|
4 |
|
|
2,5 |
|
3 |
|
20 |
|
8 |
|
|
12 |
|
||
13. |
Определить корни ХП и установить закономерность их геометриче- |
||||||||||||||||||||||||
ского расположения на комплексной плоскости. Определить t р , |
и |
п. |
|||||||||||||||||||||||
|
14. Повторить анализ, увеличив |
|
0 |
|
в 2 раза. |
|
|
|
|
|
|
|
|
|
|
||||||||||
10