
Задачник / Глава 09 (223-253)
.pdf
Глава 9 Универсальный метод определения перемещений в стержневых системах.
Метод Мора–Верещагина
9.1 Теоретическая и методическая информация. Примеры
9.1.1 Основные понятия о методе Мора–Верещагина
Универсальным методом определения перемещений в стержневых системах является применение формулы Мора. В общем случае для пространственного действия сил она имеет вид:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
i |
NFj N |
ijdz xjQxFjQxijdz |
yjQyFjQyijdz |
|||||||||||||||||||||||
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
j 1 l |
|
E j Aj |
j 1 l |
j |
|
G j Aj |
j 1 l |
j |
|
G j Aj |
||||||||||||||||
|
|
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
n |
|
M xFj M xijdz |
n |
|
|
M yFj M yijdz |
n |
|
|
M kFj M kijdz |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|||||||||
|
|
E j Ixj |
E j I yj |
|
||||||||||||||||||||||
j 1 l |
j |
|
|
j 1 l |
j |
j 1 l |
j |
|
G j I pj |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где i – характеризует положение сечения, перемещение которого определяется, и направление искомого перемещения;
j – порядковый номер участка;
n – общее число участков в заданной стержневой системе;
NFj, QxFj, QyFj, MxFj, MyFj, MkFj – выражения для внутренних усилий на j-м участке (1 j n ) от заданной нагрузки
(на это указывает индекс F);
– выражения для внутренних усилий на j-м
участке от единичной безразмерной нагрузки (на это указывает черта над буквой), приложенной в i-м сечении в направлении искомого перемещения;
lj – длина j-го участка;
νхj и νyj – коэффициенты, зависящие от формы сечения стержня на j-м участке. Для прямоугольного сечения νхj = νyj = 1,2; для кругового сечения νхj = νyj = 32/27.
223
При определении внутренних усилий от внешней нагрузки и от еди- |
|||||||||
ничной нагрузки координатные оси х и y, расположенные в сечении |
|||||||||
стержня, на каждом из участков должны быть главными центральными |
|||||||||
осями инерции, а ось z предполагается совмещенной с осью стержня. |
|||||||||
Влиянием поперечных сил на величину перемещения |
i при отно- |
||||||||
шении длины стержня к его высоте более 10 можно пренебречь, тогда в |
|||||||||
правой части формулы останется только четыре члена – первый и три по- |
|||||||||
следних. |
|
|
|
|
|
|
|
|
|
Для шарнирно-стержневых систем с узловой нагрузкой, элементы |
|||||||||
которых испытывают только деформацию растяжения–сжатия, формула |
|||||||||
для определения перемещений принимает вид: |
|
||||||||
|
|
n |
N |
Fj |
N |
ij |
l |
j . |
|
|
|
i |
|
|
|
|
|||
|
|
j 1 |
E j Aj |
|
|
|
|||
Эту формулу впервые предложил Максвелл, поэтому она носит его имя. |
|||||||||
Для прямолинейных участков стержней с постоянной жесткостью |
|||||||||
она выносится из-под знака интеграла. А. Н. Верещагиным было показано, |
|||||||||
что операцию аналитического интегрирования в этом случае можно заме- |
|||||||||
нить графоаналитической операцией, так называемым «перемножением |
|||||||||
эпюр», заключающимся в том, что площадь F эпюры усилий на рассмат- |
|||||||||
риваемом участке стержня от заданных сил умножается на ординату ηi |
|||||||||
эпюры на том же участке, построенной от единичной силы, соответствую- |
|||||||||
щей искомому перемещению. Ординаты на единичной эпюре берутся в тех |
|||||||||
сечениях, где располагаются центры тяжести площадей эпюр от заданной |
|||||||||
нагрузки. |
|
|
|
|
|
|
|
|
|
|
|
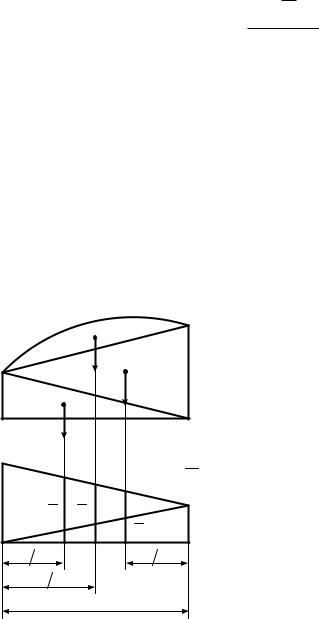
Эп. МF |
|
|
|
Эпюра от внешней нагрузки мо- |
|||
|
|
жет быть и линейной, и криволиней- |
|||||||
а) |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ной (так, в случае равномерно распре- |
||||||
|
F 2 |
b |
деленной нагрузки эпюра изгибающих |
||||||
|
моментов очерчена квадратной пара- |
||||||||
а |
|
F 3 |
|||||||
|
|
болой). Эпюра от единичной силы |
|||||||
|
|
|
|||||||
|
F1 |
|
может быть только линейной в преде- |
||||||
б) |
|
|
лах одного участка (рис. 9.1). |
||||||
|
|
|
|
|
В |
общем случае на |
некотором |
||
|
|
Эп. М i |
|
|
|
||||
|
|
участке стержня перемножение эпюр, |
|||||||
с |
|
|
|||||||
1 2 |
|
когда одна из них очерчена квадрат- |
|||||||
|
d |
||||||||
|
|
ной параболой, производится так: де- |
|||||||
|
|
3 |
|||||||
l |
3 |
l 3 |
лим эпюры на составные части – тре- |
||||||
|
l 2 |
|
угольники и квадратную параболу, |
||||||
|
l |
|
площади и центры тяжести которых |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
легко определимы. Центр тяжести |
||||||
|
Рис. 9.1 |
|
треугольника располагается на рас- |
||||||
|
|
стоянии 1/3 высоты от основания тре- |
|||||||
|
|
|
|||||||
224 |
|
|
|
|
|
|
|
|
|
угольника, а у параболы, как у симметричной фигуры, – посередине (см. рис. 9.1). Тогда
ωF η ωF1η1 ωF 2η2 ωF 3η3 ;
|
|
ω |
|
|
|
al / 2 ; |
ω |
bl / 2 ; ω |
ql3 /12 |
, |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
F1 |
|
|
|
|
|
|
|
|
|
|
|
|
F 3 |
|
|
|
|
|
|
F 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где q – распределенная нагрузка на данном участке стержня; |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
η |
2 |
c |
1 |
d ; |
|
|
η |
1 |
c |
2 |
d ; |
η |
1 |
c |
1 |
d . |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
1 |
3 |
|
|
|
3 |
|
|
|
|
3 |
3 |
|
3 |
|
|
2 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
9.1.2 |
Перемещения в шарнирно-стержневых системах |
||||||||||||||||||||||||||||||||||||||||
Пример 9.1.1. Найти полное перемещение нижнего узла двухстерж- |
|||||||||||||||||||||||||||||||||||||||||
невой системы, изображенной на рис. 9.2, а. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
70 ; |
|
2 |
|
30 ; |
h = 2 м; |
F = 40 кН; |
A1 = 1,3 см2; |
|
A2 = 2,4 см2; |
||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
E 2 105 МПа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
l1 h / cos 1 2 / cos70 5,848м; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
l2 h / cos 2 2 / cos30 2,309 м. |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
2 2 |
|
h |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
В шарнирно-стержневых системах с |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
нагрузкой, приложенной в узлах, все |
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
элементы работают только на растя- |
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
жение–сжатие. Следовательно, в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
формуле |
Мора |
|
ненулевым |
будет |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
лишь один член: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
n |
|
|
|
|
NFj Nijdz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
|
|
|
|
E j Aj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
j 1 l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а так как в пределах каждого из |
в) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
стержней j жесткости Еj Aj |
и про- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
дольные силы |
NFj , Nij остаются по- |
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
стоянными, то выражение принимает |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||||||||||||||||||||||||
вид формулы Максвелла: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
n |
NFj Nijl j |
|
|
|
|
|
|
|
|
|
|
|
Рис. 9.2 |
|
|
|
|
|
|
|
|||||||||||||||||||
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
E j Aj |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Для определения полного перемещения узла надо найти вертикальную и горизонтальную составляющие искомого перемещения.
225
Изобразим |
|
|
два |
вспомогательных единичных |
|
загружения |
системы |
|
|||||||||||||||||||||||||||||||||||||||||
(рис. 9.2, б, в). Затем найдем усилия в стержнях системы от заданной на- |
|
||||||||||||||||||||||||||||||||||||||||||||||||
грузки и от каждой из единичных сил в отдельности (рис. 9.3). |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 9.3, а: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
а) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X 0 ; |
|
|
NF1sin 1 NF 2sin 2 |
0 ; |
|
||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
2 |
NF2 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
NF1 |
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
NF1 NF 2 |
sin 2 |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
1 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
Y 0 ; |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
NF1cos 1 |
NF 2cos 2 |
F . |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставив NF1, выраженное через NF 2 , |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
Nв2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
N |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
находим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
в1 |
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
40 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
NF 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 2 |
cos |
2 |
|
sin30 |
cos30 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg 1 |
|
|
|
|
|
tg70 |
|
|
|
|
|||||||||||||||
в) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
1 |
|
|
2 |
|
Nг 2 |
|
|
|
|
38,17 кН; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Nг1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 30 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
38,17 |
20,31 кН. |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
F1 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 70 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 9.3, |
б: |
|
|
по аналогии с пре- |
|
|||||||||||||||||||||
|
|
|
|
Рис. 9.3 |
|
|
|
|
|
|
|
|
|
|
|
|
дыдущим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
0,954 ; |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Nв2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 2 |
|
cos |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tg 1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin 2 |
|
0,508. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
в1 |
в2 sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определяем вертикальную составляющую искомого перемещения:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
NFj Nвjl j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
|
|
N |
F1 |
N |
l |
N |
F 2 |
N |
в2 |
l |
2 |
|
|
|||||||
|
в |
|
|
|
|
|
|
|
|
в1 1 |
|
|
|
|
|
|
|
|||||
|
E j Aj |
|
|
|
|
|
|
|
|
EA2 |
|
|
|
|||||||||
|
j 1 |
|
|
|
EA1 |
|
|
|
|
|
||||||||||||
|
20,31 0,508 5,848 |
|
|
38,17 0,954 2,309 |
|
|||||||||||||||||
|
2 105 103 1,3 10 4 |
|
|
|
2 105 103 2,4 10 4 |
|
||||||||||||||||
23,21 10 4 17,52 10 4 4,073 10 3 м 4,073 мм.
Рисунок 9.3, в:
Y 0 ; Nг1cos 1 Nг2cos 2 0 ;
Nг1 Nг 2 cos 2 ;
cos 1
226
X 0; |
Nг1sin 1 |
Nг2sin 2 1 0 . |
|
|
|
|||||||
Решая уравнения равновесия, находим: |
|
|
|
|||||||||
|
|
|
|
|
Nг1 0,879; |
Nг2 0,347. |
|
|
||||
Определяем горизонтальную составляющую перемещения: |
|
|
||||||||||
|
|
г |
NF1Nг1l1 NF 2 Nг 2l2 |
|
20,31 0,879 5,848 |
|
|
|||||
|
|
|
|
EA |
EA |
|
2 105 103 |
1,3 10 4 |
|
|
||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
38,17 ( 0,347) 2,309 |
|
|
|
||||
|
|
|
|
|
2 105 103 2, 4 10 4 |
|
|
|
||||
|
40,15 10 4 6,37 10 4 33,78 10 4 м 3,38 мм. |
|
||||||||||
Находим полное перемещение: |
|
|
|
|
|
|
||||||
|
|
|
|
в2 2г 4,072 3,382 5, 29мм. |
|
|
||||||
Ответ: |
= 5,29 мм. |
|
|
|
|
|
|
|
||||
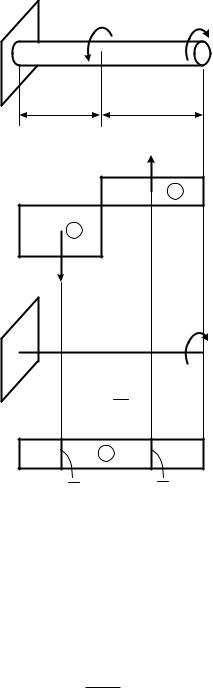
Пример 9.1.2. В заданной плоской ферме (рис.9.4, а) определить |
||||||||||||
вертикальное перемещение загруженного узла. |
|
|
|
|||||||||
Дано: l = 2 м; h = 1 м; |
|
|
|
|
|
|
|
|||||
A12= A23 = 34,94 см2; |
|
|
|
|
2 |
|
|
|||||
|
|
|
|
|
2 |
|
|
а) |
|
|
|
|
A24 = A14 = A13 = 31,25 см ; |
|
|
|
|
|
|
|
|||||
|
5 |
|
|
|
|
|
|
|
|
|
|
h |
E 2 10 МПа; |
F = 500 кН. |
|
R |
|
|
Rb |
||||||
|
С |
|
|
|||||||||
Решение. |
Перемещение узла |
|
|
|
|
|
||||||
|
С |
|
|
|
|
|||||||
4 ищем по |
|
формуле Максвелла. |
|
1 |
4 |
3 |
В |
|||||
|
|
|
||||||||||
Наряду с заданным рассматриваем |
|
|
|
F |
|
|
||||||
|
|
l |
l |
|
|
|||||||
единичное |
состояние системы – |
|
|
|
|
|||||||
|
|
|
|
|
|
|||||||
загружение фермы в узле 4 верти- |
|
|
|
2 |
|
|
||||||
кальной единичной силой (рис 9.4, |
|
б) |
|
|
|
|||||||
|
|
|
|
|
||||||||
б). Находим усилия во всех стерж- |
|
|
|
|
|
|
||||||
нях фермы в каждом из двух за- |
|
|
|
|
|
|
||||||
гружений методом вырезания уз- |
|
1 |
|
4 |
|
3 |
||||||
|
|
|
|
|
|
|||||||
лов. |
|
|
|
|
|
|
|
|
|
1 |
|
|
Рассмотрим |
заданное |
со- |
|
|
|
|
|
|
||||
стояние. |
|
|
|
|
|
|
|
|
|
Рис. 9.4 |
|
|
|
|
|
|
|
F 250 |
|
|
|
|
|
|
|
Реакции R |
R |
кН. |
|
|
|
|
|
|
||||
|
С |
|
|
B |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вырезаем узел 1 (рис. 9.5, а): |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
tg h 0,5 ; |
26,57 . |
|
|
|
|||
|
|
|
|
|
|
l |
|
|
|
|
|
|
Составляем уравнение равновесия узла 1: |
|
|
|
|||||||||
227
Y 0; N12F sin RC 0;
N F |
|
RС |
|
250 |
559,02 кН; |
|
|
||||
12 |
|
sin |
|
sin26,57 |
|
|
|
|
|
X 0; N12F cos N14F 0;
N14F N12F cos 559,02cos26,57 500кН.
Вырезаем узел 4 (рис. 9.5,
а) |
|
|
|
|
|
|
N12F |
|
||
1 |
|
|
|
|
|
|
|
х |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N F |
|
|||
|
|
|
|
|
|
|
|
|||
|
|
|
RС |
14 |
|
|||||
y |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
N24F |
|
|||
б) |
N14F |
|
|
|
||||||
|
|
|||||||||
|
|
4 N43F |
х |
|||||||
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
F
y
Рис. 9.5
б):
Y 0 ; N24F F 500 кН;
X 0 ; N14F N43F 500кН.
Узел 3 аналогичен узлу 1. Следовательно,
N23F N12F .
Рассмотрим единичное состояние. Загружение аналогично заданному, по-
этому все усилия определяются по тем же зависимостям, но будут в F раз меньше и безразмерны:
RС RB 0,5; N12 N23 1,118; N24 1;
N14 N43 1.
Кроме того, учтем, что l14 = l43 = 2 м; l24 = 1 м;
l12 l23 
 l142 h2
l142 h2 
 22 12
22 12 
 5 2,24 м.
5 2,24 м.
Подсчитываем по формуле Максвелла перемещение узла 4:
|
|
|
|
|
|
|
|
N F |
|
|
|
|
|
|
N F |
|
|
|
|
N F |
|
|
|
|
|
|
|
|
||
|
|
|
|
NFj N jl j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
5 |
|
N l |
|
|
|
N l |
N |
24 |
l |
24 |
|
|
||||||||||||||||
4 |
|
|
|
2 |
|
12 |
12 12 |
2 |
|
14 |
|
14 14 |
|
24 |
|
|
|
|
|
|||||||||||
E j Aj |
|
EA12 |
|
|
|
|
|
EA24 |
|
|
|
|||||||||||||||||||
|
j 1 |
|
|
|
|
|
|
EA14 |
|
|
|
|
||||||||||||||||||
2 |
559,02 1,118 2,24 |
2 |
|
|
|
500 1 2 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
2 108 |
34,94 10 4 |
|
|
|
|
2 108 31,25 10 4 |
|
|
|
|||||||||||||||||
|
|
|
|
500 1 1 |
|
40,06 |
10 4 |
32 10 4 8 10 4 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
108 31,25 10 4 |
|
||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
80,06 10 4 м 8,006 мм. |
|
|
|
|
|
|
|
|
|
||||||||||||||
Ответ: 4 |
8,006 мм. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
228
9.1.3 Углы закручивания при кручении стержней
Пример 9.1.3. Для стержня, загруженного крутящими моментами (рис. 9.6, а), определить угол поворота сечения В.
Известна жесткость стержня при кручении GIp=1400 кНм2. При решении применим метод Мора–Верещагина.
а) |
|
mк1 40кНм mк2 |
10кНм |
|
C |
|
|
|
B |
|
|
2м |
3м |
|
|
|
Эп. МкF, кНм |
|
|
|
|
|
к2 |
|
б) |
|
|
- |
10 |
|
|
|
|
|
|
|
+ |
|
|
|
30 |
к1 |
|
|
|
|
|
|
|
в) |
|
|
|
|
|
|
|
|
1 |
г) |
|
Эп. М к |
|
|
1 |
|
|
1 |
|
|
- |
|
||
|
|
|
|
|
|
|
1 |
2 |
|
|
|
Рис. 9.6 |
|
|
Решение. В формуле Мора в этом случае остается один член
|
1 |
n |
|
|
|
θB |
MкFj M |
кBj dz . |
|||
|
|||||
|
GI p j 1 l |
||||
|
|
j |
|||
С использованием приема Верещагина формула принимает вид:
θB 1 n ωкjηBj .
GI p j 1
229

Строим эпюры крутящих моментов от заданных сил (рис.9.6, б) и в единичном состоянии при приложении в сечении В единичного крутящего момента (рис. 9.6, в, г). Перемножим эпюры MкF и Mк :
θB GI1 p 30 2 1 10 3 1 140030 2,14 10 2 рад.
Минус в ответе показывает, что поворот сечения В произошел в сторону, противоположную направлению единичного момента.
Ответ: θB 0,0214 рад.
9.1.4 Перемещения в балках
|
|
|
|
Пример 9.1.4. В заданной балке (рис. 9.7, а) найти прогибы в точках |
|||||||||||||||||||||||||||||||||||||||||||||
С и D и угол поворота сечения А двумя способами: |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1) по формуле Мора без использования приема Верещагина; |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2) по формуле Мора с использованием приема Верещагина. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Дано: m =50 кНм; |
|
q = 10 кН/м; |
F = 40 кН; |
l = 4 м; |
а = 1 м; |
||||||||||||||||||||||||||||||||||||||||
EIx = 7600 кНм2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
m |
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 . |
|
Решение по |
формуле |
|||||||||||||
а) |
|
|
|
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
Мора. В |
данной задаче |
имеем |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
|
F |
C |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дело с плоским поперечным из- |
|||||||||||||||
|
A |
|
|
|
|
|
|
|
l 2 |
|
|
D |
|
|
|
|
|
z1 |
|
z |
гибом. Изгибающих моментов и |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
а |
|
|
поперечных сил в горизонталь- |
||||||||||||||||||||||
|
RАF |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ной |
плоскости нет, продольная |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
RВF |
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
б) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сила |
и крутящий момент тоже |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
RВС |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отсутствуют. |
Поперечной силой |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
АС |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
|
|
|
|
|
|||||||||||||||
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
в вертикальной плоскости при |
||||||||||||||
|
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z1 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
в) 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
определении |
прогиба |
|
|
можно |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пренебречь. Следовательно, в |
||||||||||
|
|
|
|
|
|
|
|
RАА |
|
|
|
|
|
|
|
|
RВА |
|
|
В |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
формуле |
Мора остается |
только |
|||||||||||||||||||||||
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z1 |
один член |
n |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
г) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
M Fj Mijdz . |
||||||||
|
RАD |
|
|
|
l 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
EI x |
||||||||||||||||||||||||||||
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
ВD |
|
В |
|
|
|
C |
|
|
j 1 l j |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
z1 |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
Для определения искомых |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
перемещений надо рассмотреть |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
три единичных загружения, ука- |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 9.7 |
|
|
|
|
|
|
|
занных на рисунке 9.7, б, в, г. |
||||||||||||||||||||
230 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Первое – для определения прогиба в сечении С, второе – для определения угла поворота сечения А, третье – для определения прогиба в сечении D.
а) Заданное состояние. Определяем реакции:
|
|
|
|
M B 0; RAF l |
ql2 |
m Fa 0; |
|||||||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
R |
|
|
|
|
ql 2 |
/ 2 m Fa |
|
80 50 40 |
2,5 кН; |
||||||||
AF |
|
l |
|
|
4 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
M A 0; RBF l m |
ql2 |
F (a l) 0 ; |
|||||||||||||
|
|
2 |
|||||||||||||||
|
|
m ql 2 / 2 F a l |
|
|
|
|
|
|
|||||||||
R |
|
|
50 80 200 |
82,5 кН. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
BF |
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Проверка: RAF RBF ql F 0 ; |
|
|
|
||||||||||||||
|
|
|
|
2,5 82,5 10 4 40 0; |
0 0. |
|
|||||||||||
Пишем уравнения изгибающих моментов:
|
|
0 z1 a; |
M1F Fz1 ; |
|||||||
0 z |
|
l; M |
|
R |
|
z |
|
m |
qz22 |
. |
2 |
2 F |
AF |
2 |
|
||||||
|
|
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
||
б) Рассмотрим единичное состояние для определения прогиба в точке С. Из уравнений равновесия балки находим реакции:
|
|
|
|
a |
|
|
|
|
a l |
. |
|
R |
AC |
; |
R |
||||||||
|
|
||||||||||
|
|
|
l |
|
|
BC |
l |
||||
|
|
|
|
|
|
|
|
||||
Составим уравнения изгибающих моментов:
|
|
0 z1 a ; |
|
|
|
1С z1 ; |
|
|
|
||||||||
|
|
M |
|
|
|
||||||||||||
0 z |
|
l ; |
|
|
|
|
|
z |
|
|
a |
z |
|
|
|||
2 |
M |
2С |
R |
AC |
2 |
2 |
. |
||||||||||
l |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Определяем прогиб в точке С:
|
|
|
|
1 |
a |
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
υС |
|
|
|
|
M1F M1С dz M 2 F M 2С dz |
|
|
|
|
|
||||||||||||||
|
EI |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 a |
|
|
|
|
|
|
l |
|
|
|
|
qz2 |
|
|
|
a |
|
|
|
||||||
|
|
Fz1 z1 dz |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
m |
|
|
|
|
|
|
z2 |
dz |
|||||||||||||||
|
RAF z2 |
|
2 |
|
l |
|||||||||||||||||||||
|
EI 0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 Fa3 |
|
RAF al 2 |
m al |
|
|
qal3 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
EI |
3 |
|
|
3 |
|
2 |
|
8 |
|
|
|
|
|
|
|
|
|||||||
231
|
1 |
|
|
40 13 |
2,5 1 42 |
50 1 4 |
10 1 43 |
|
||||||||||
|
|
|
|
3 |
|
|
|
3 |
|
2 |
|
|
|
8 |
|
|
||
|
EI |
|
|
|
|
|
|
|||||||||||
|
|
|
6,67 |
|
6,67 |
8,772 10 4 |
м 0,877мм. |
|
||||||||||
|
|
|
EI |
7600 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
в) Рассмотрим единичное состояние для определения угла поворота сечения А.
Из уравнений равновесия балки (рис. 9.7, в) находим
|
|
|
|
1 |
|
|
|
|
1 |
. |
|
R |
AA |
; |
R |
||||||||
|
|
||||||||||
|
|
|
l |
|
|
BA |
l |
||||
|
|
|
|
|
|
|
|
||||
Пишем уравнения изгибающих моментов по участкам:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 z1 a; |
|
|
|
|
|
|
|
1A 0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 z |
|
l; |
|
|
|
|
|
|
|
1 |
|
|
|
|
z |
|
|
1 |
z2 |
. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
M |
2 A |
R |
AA |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Определяем угол поворота сечения А: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qz |
2 |
|
|
|
|
|
|
z |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
θ |
|
|
|
|
|
|
|
|
M |
|
M |
|
dz |
|
|
|
|
|
|
|
R |
|
|
z |
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
dz |
||||||||||||||||||||||||||||
|
A |
|
|
|
|
|
|
|
|
|
|
2F |
|
|
|
|
|
2 A |
|
|
EI |
|
|
|
|
AF |
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
l |
|
|
|||||||||||||||||
|
|
|
|
EI 0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
RAF l |
3 |
|
|
m l |
2 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
1 |
|
RAF l |
|
|
m l |
ql |
|
|
|
|
|
|
|
|
|
ql |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
EI |
|
2 |
|
|
|
|
|
|
|
|
|
|
3 2 |
|
|
|
3l |
|
|
|
|
|
|
|
2l |
|
|
|
|
|
|
4 2 l |
|
|
|
|||||||||||||||||||||||||
|
1 |
|
|
|
2,5 16 |
50 4 |
10 64 |
|
2,5 64 |
|
50 16 |
|
10 64 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
3 2 |
|
|
|
|
|
3 4 |
|
|
|
2 |
4 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 4 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
66,67 |
|
|
66,67 |
8,772 10 3 рад. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EI |
|
7600 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
г) Для определения прогиба в середине пролета (сечение D) в единичном состоянии прикладываем вертикальную единичную силу в точке D
(рис. 9.7, г).
|
|
|
|
|
|
|
|
|
|
|
1 |
. |
|||
Реакции R |
AD |
R |
BD |
||||||||||||
|
|||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В единичном состоянии балка имеет три участка. Составляем урав- |
|||||||||||||||
нения моментов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 z1 a; |
|
|
|
1D 0 ; |
|||||||||||
|
M |
||||||||||||||
0 z2 l / 2; |
|
|
|
|
|
|
|
2 D z2 / 2; |
|||||||
|
|
|
M |
||||||||||||
l / 2 z3 l ; |
|
|
|
|
3D z3 / 2 1 z3 l / 2 l z3 / 2 . |
||||||||||
|
|
M |
|||||||||||||
232
