Лекции по Математическому Анализу 1 курс ИПММ лектор Моисеев / matan

Добавил:

FilimonLipin86 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский политехнический университет Петра Великого (бывш. СПбГПУ)

Предмет:

Математический анализ

Файл:

F x g ax b a,

F x g ax b a

.pdf

Скачиваний:

132

Добавлен:

18.10.2017

Размер:

6.76 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 127 8 9 10 11 12 > Следующая >>>

dG x		, h G x			h f x		g x		f x		0	g x	0	h
	0			0		0		0			0		0
	f x		h g x	f x		g x		h df x		, h g x			f x		dg x	, h
		0	0		0	0			0			0		0	0

Следствие. Дифференцирование линейной комбинации

Пусть f , g — функции, заданные в некоторой окрестности точки точке; G f g .

Тогда функция G дифференцируема в точке x0 ,
	x0	f	x0		x0	,
G				g

x	0

и дифференцируемые в этой

(5)

Теорема 3. Дифференцирование частного

Пусть

f ,

— функции, заданные в некоторой окрестности точки

точке,

;

H .

Тогда функция H

дифференцируема в точке

x0 ,

f x0 g x0 f x0 g x0

g x 2

и дифференцируемые в этой

. (6)

Доказательство

H x H x				f x		f x				f	x			f	x				f	x			f x
H x H x				g x		0				g x					0				g	0				0
		0		g x		g x				g x				g x					g	x			g x
		0
						0																		0
H x H x				1	f x f				x					f x					g x g x
		0								0					0									0
	x x			g x		x x							g x g			x					x x
		0						0										0					0
H x H x		1	f x			f	x					g	x				f x			g x				f	x		g x
0			f x					0				g	x						0			0				0	0
0								0											0			0				0	0
x x	0	g x		0		g x	g		x					0							g x					2
0	x x	0		0		0				0				0							g x					2
	x x
																							0

§ 4 Производная обратной функции

Теорема 1

Пусть функция f

определена, непрерывна и строго монотонна на интервале

;

c, d f a, b f x0 0 .

f	1	: c,

d a,

;

x	a,
0

, а

дифференцируема в точке x0 ,

Тогда функция

дифференцируема в точке

g y
	0
dg x
0

	f
	f

df

x0 , 1

(1)

Доказательство

Заметим, что по теореме об обращении строго монотонной непрерывной функции функция

непрерывна на интервале c, d .

Мы должны показать, что

g y

(2)

y y

y y0

d , yn

y0 ,

yn y0 и положим

Возьмем произвольную последовательность yn

n 1

xn g yn . Тогда xn a,

b , xn

, xn

;

xn yn .

g y

f x

Дифференциал функции f

есть операция умножения на f

, а дифференциал g —

умножение на обратное число

. Указанные умножения нейтрализуют друг друга,

дифференциалы — взаимно обратные линейные функции.

§ 5 Дифференцирование сложной функции

Теорема 1

Пусть	f	— функция, определенная в окрестности точки				x0	и дифференцируемая в этой точке;
— функция, определенная в окрестности точки			y	0	f	x	и дифференцируемая в этой точке;
— функция, определенная в окрестности точки				0		0	и дифференцируемая в этой точке;
F g		f : F x g f x .

Тогда F — дифференцируема в точке x0 ,

F x0 g y0 f x0 .

(1)

Доказательство

Мы должны показать, что

F x

x F x

g y

f x

Запишем приращение функции

в виде

где 0 0 lim y .

y 0

Возьмем произвольную последовательность

0, xn

0 . Положим

n 1

Тогда

Теперь

0 .

Формула (3) дает нам

F x0 xn F x0 g y0 yn yn yn ,

F x x

F x

y0 yn

x0 .

Теорема 2 Об инвариантности формы дифференциала

В условиях теоремы 1 дифференциал композиции равен композиции дифференциалов,

dF x0 dg y0

df x0

, x

x ,

Доказательство

, x

x g

, x

, df

В традиционных обозначениях

z g y , dz g y dy ,

dy — дифференциал независимой переменной y .

(2)

(3)

(4)

(5)

(6)

	z g y , y f x , z g f x F x , dz F	x
	z g y , y f x , z g f x F x , dz F	x
dy	— дифференциал функции y f x .

Дифференциал инвариантен по форме — внешне выражения

dx g y f

(6) и (7) для

dx g y dy

совпадают.

,(7)

§ 6 Таблица производных

f x

1.	C
2.	x
3.	x	n

4.	x

5.	e	x

6.	ln x
7.	sin x
8.	cos x
9.	tg x
10.	ctg x

11.	arcsin x
12.	arccos x
13.	arctg x

14.	arcctg x

nxn 1

x 1

	e		x
	e
		1
		x
	cos x
sin x
		1
cos			2		x
cos					x
			1
				2
	sin			2		x
	sin					x
		1
	1 x
					2
			1
							2
	1 x						2
		1

1 x2
			1
		x				2
1		x

Доказательство

Формулы 12 получены раньше.

Третью формулу можем получить индукцией:

	x x				x
4)	x x				x
4)			x
			x
	e	x x	e	x
5)	e		e		e
5)		x			e
		x

6) Пусть f x

x	g		y	0	. По
0

xn1

xn x

n xn1x xn1 n xn xn

n 1

x 0

1 e

ex , g f 1

: g y ln y . Возьмем произвольную точку

теореме о производной обратной функции

, положим

sin

7) sin

8) f

g y	1	1	.
	f x0
0		y0

x x sin x 2 sin x cos x x ;

2 2

x x sin x	2 sin		x			x
	2 sin		2
			2	cos	x		cos x
x		x		cos	x	2	cos x
x		x				2	x0
							x0
x cos x sin
x cos x sin		x .
	2

По теореме о дифференцировании композиции

f x

9) f x tg x cossin xx .

f x cos

cos		x	1	sin x
cos		x	1	sin x
	2

x cos x sin x sin x cos2 x

cos2 x

11)	g

y arcsin

, f g 1 :

f x sin x .

Пусть y	0	1, 1 ,	x	g y	0	, тогда		y	0	f x
	0		0		0				0		0
По теореме о производной обратной функции
				g y0			1				1

							f x0				cos x0
							f x0				cos x0

sin x0 .

1	1	.


1 sin2 x	1 y2
0	0

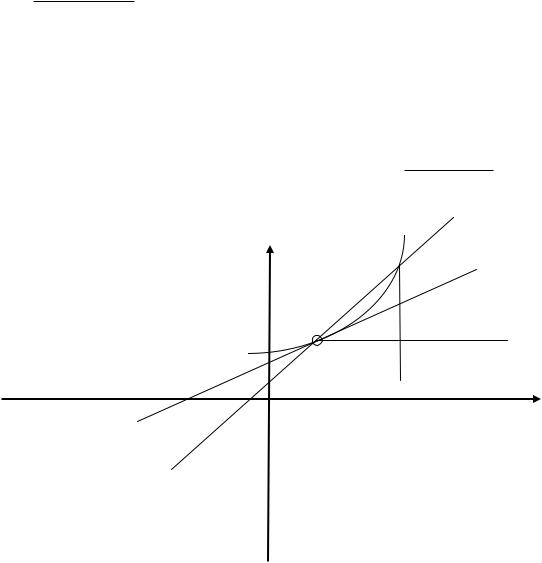
§ 7 Механический и геометрический смысл производной и дифференциала

10. Пусть x x t — закон движения точки,

движущейся по прямой, тогда x x t t

xx t

x t

— координата в момент t точки,

— путь пройденный точкой за период

t, t t ,	x t t x t				t		— мгновенная скорость в

		t	— средняя скорость за этот период, x

момент t ,		t dt — путь, который точка прошла бы за время				dt	, если бы двигалась
	dx x
равномерно со скоростью, равной мгновенной скорости в момент t .
20. Пусть — график непрерывной функции на отрезке a, b ,				M	0	x0 , y0 , y0 f x0 ,
x a, b ,	M x,	f x	— соответствующая точка графика. Прямая M 0 M называют секущей

графика, она проходит через точку

M	0

и имеет угловой коэффициент

f	x
	0
x
0

M K N

Устремим M M0 , M . Если функция имеет производную в точке x0 , угловой коэффициент имеет эту производную своим пределом. Секущая имеет некоторое предельное положение.

Предельное положение секущей называется касательной. Касательная — это прямая с угловым

коэффициентом f		x0	, проходящая через точку	M		x	,	f x		. Уравнение касательной имеет
коэффициентом f		x0	, проходящая через точку		0	0		0		. Уравнение касательной имеет

вид

y y	0
	0

x	0	x
	0

x	0
	0

Приращение функции ( y ) — это приращение			NM	ординаты точки графика функции,
соответствующее приращению x M	0 N	абсциссы. Дифференциал dy			f	x dx	—
соответствующее приращению x M	0 N	абсциссы. Дифференциал dy			f	x dx	—
приращение NK ординаты точки касательной.
Если l — касательная, то
M ,	l		M , M0 .
	M ,M		M
			0

(*)

Это следует из представления приращения дифференцируемой функции. Соотношение (*) однозначно определяет прямую l . Мы привели, таким образом, альтернативное определение касательной, основанное на понятии дифференцируемой функции, в отличие от первого описания в терминах производной.

§ 8 Производные и дифференциалы высших порядков

10. Определение

Пусть функция

имеет производную во всех точка некоторой окрестности точки

x	0

. Положим

f :		x		f		x	. Если функция

производной второго порядка функции

имеет производную x0 , эту производную называют

f	в точке		x0	и обозначают
	x	y		d	2	y
f							.
						2
	0			dx

Итак, вторая производная — это производная от производной:

f x
0

По индукции определяем производные последующих порядков:

f		0
	n

Производные обозначают через

		0
n 1		x

f ,

— производная

	f	IV	,	f	V	,	f	VI	.
,

-го порядка.

Если x x t — закон движения точки, то a d 2 x — ускорение. dt 2

Второй дифференциал — дифференциал дифференциала:

d 2 f x0 , x d df , x x0 , x f x0 x2 .

Если y f x , то dy f x dx, d 2 y f x dx2 , d 3 y f x dx3 ,

20. Основные свойства производных высших порядков.

f	n	m
		m

n m

2) Дифференцирование линейной комбинации.

f g	n	f	n	g	n

3) Формула Лейбница

f g	n	n
	n	k	f
		Cn	f
		k 0

nk	g	k
	g

Внешне формула Лейбница напоминает бином Ньютона и аналогичным образом доказывается. Произведение двух функций диффференцируется поочередным дифференцированием

сомножителей. При вычислении производной

-го порядка мы на каждом из n

шагов

выбираем для дифференцирования первый или второй сомножитель. Для получения члена вида

f	nk	g	k	следует выбрать второй сомножитель на k шагах из n возможных. Такой выбор

				k	способами. Формально доказательство легко проводится по индукции. Правило
реализуется Cn

вычисления производной произведения — база индукции. Проведем индукционный переход.

n 1

nk 1

k 1

f g

k 0

nk 1

n 1

k 1

nk 1

n 1

k 1

nk 1

f g

n 1

g Cn

k 0

k 1

n 1

nk 1

Cn 1 f

k 0

30. Таблица производных

1) Для m

имеем


x		n		m m 1	m n 1	x	mn	, n m,
							mn
	m


			0, n m

Для других показателей

	x		n
	x			1

2)	e	x	n	e	x	.

n 1

x	n 1

3) sin x	n		n	,	cos x	n		n
3) sin x		sin x		,	cos x		cos x	.
			2					2

Действительно,

									2	,
sin x	cos x sin x		, cos x	sin x	2		sin x	2	2	,
		2			2	2		2

Заметим еще, что

sin x;

sin x

cos x, sin x sin x, sin x cos x, sin x

sin x, cos x

cos x.

cos x

sin x, cos x

cos x, cos x

40. Дифференцирование сложной функции.

Пусть F x g f x — сложная функция. Тогда

F x g f

x f x ,

f x f x

F x g f x

x g

В простейшем случае, где

ax b

получим.

Повторим дифференцирования в терминах дифференциалов. Если

z g y , y

, то

dy g y dy,				g y d		y
d	2	y g y dy	2		2

Наличие второго слагаемого означает нарушение инвариантности формы второго

дифференциала. Если	y ax b	— линейная функция, то d	2	y 0	, d	n	z f	n	y

дифференциал остается инвариантным по форме.

dyn

-й

§ 9 Дифференцирование функций, заданных параметрически и неявно

1 . Пусть ,

— непрерывные функции на отрезке

. Рассмотрим отображение

отрезка

в координатную плоскость

Oxy

, которое переводит

t ,

в точку

под

Отображение называется путем на плоскости. Образ , отрезка

действием отображения — кривая на плоскости. Если эта кривая является графиком некоторой функции f , то говорят, что функция f параметрически задается системой уравнений

x t ,y t .

Функции

, , f

связаны соотношением

: t


		t		, t ,

В частности, если

— строго монотонная функция, то

	1

Если функции ,

дифференцируемы в точке t0 ,

, то функция

дифференцируема в точке

Действительно, по теореме о производной обратной функции

имеет производную,

, а по теореме о производной сложной функции имеет производную функция

и справедлива доказываемая формула.

Если предположить, что функции

дважды дифференцируемы в точке t0

, то функция

дважды дифференцируема в точке

x0 ,

1 x

Действительно, f

x 1 x ,

В традиционных обозначениях пишут

t t t

d 2 y

dx dx

20. Пусть F — функция двух переменных.

<<< < Предыдущая 1 2 3 4 5 67 / 127 8 9 10 11 12 > Следующая >>>