
- •Условие изоморфизма конечномерных линейных пространств
- •Матрица перехода к новому базису, изменение координат вектора.
- •Формула для размерности суммы двух подпространств
- •Прямая сумма подпространств, различные определения
- •Линейное отображение векторных пространств, ядро и образ.
- •Матрица линейного отображения (оператора), переход к новому
- •Собственные векторы и собственные значения линейного оператора а, способы их нахождения.
- •Существование одно- или двумерного инвариантного подпространства относительно оператора, действующего в вещественном пространстве
- •Критерий диагонализируемости линейного оператора
- •Жорданова форма матрицы. Алгоритм нахождения Жордановой нормальной формы матрицы.
- •Сопряженное пространство, дуальные базисы, второе сопряженное пространство
- •Билинейные функции и формы, изменение матрицы при переходе
- •Алгоритм Лагранжа для приведения квадратичной формы к
- •Закон инерции вещественных квадратичных форм.
- •Положительно определенные квадратичные функции. Критерий Сильвестра.
- •Евклидовы пространства, условие изоморфизма.( не точно!)
- •Неравенство Коши-Буняковского. Модуль вектора, расстояние и косинус угла между векторами.
- •Процесс ортогонализации Грама-Шмидта
- •Ортогональное дополнение к подпространству евклидова пространства.
- •Ортогональные операторы и ортогональные матрицы. (не весь!)
- •Простейший вид матрицы ортогонального оператора евклидова пространства.
- •Сопряженные операторы
- •Симметрические операторы и симметрические матрицы.
- •Существование ортогонального базиса из собственных векторов симметрического оператора
- •Норма оператора. Норма симметрического оператора.
- •Приведение квадратичной формы ортогональным преобразованием к главным осям
- •Приведение пары форм к диагональному виду
- •Число обусловленности матрицы. Связь с приближенным решением систем линейных уравнений
-
Алгоритм Лагранжа для приведения квадратичной формы к
диагональному виду.
Данный метод состоит в последовательном выделении в квадратичной форме полных квадратов. Пусть

есть данная квадратичная форма. Возможны два случая:
-
хотя бы один из коэффициентов
 при
квадратах отличен от нуля. Не нарушая
общности, будем считать
при
квадратах отличен от нуля. Не нарушая
общности, будем считать (этого
всегда можно добиться соответствующей
перенумерацией переменных);
(этого
всегда можно добиться соответствующей
перенумерацией переменных); -
все коэффициенты
 ,
но есть коэффициент
,
но есть коэффициент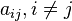 ,
отличный от нуля (для определённости
пусть будет
,
отличный от нуля (для определённости
пусть будет ).
).
В первом случае преобразуем квадратичную форму следующим образом:
![]()
![]()
![]()
где ![]() ,
а через
,
а через![]() обозначены
все остальные слагаемые.
обозначены
все остальные слагаемые.![]() представляет
собой квадратичную форму от n-1 переменных
представляет
собой квадратичную форму от n-1 переменных![]() .
.
С ней поступают аналогичным образом и так далее.
Заметим,
что ![]()
Второй
случай заменой переменных ![]() сводится
к первому.
сводится
к первому.
-
Закон инерции вещественных квадратичных форм.
Число
положительных коэффициентов в нормальном
виде квадратичной формы называемое
положительным индексом инерции; число
отрицательных коэффициентов называемое
отрицательным индексом инерции и число
нулевых коэффициентов называемое
дефектом квадратичной формы являются
инвариантами, т.е. не зависят от базиса,
в котором данная квадратичная форма
принимает нормальный вид.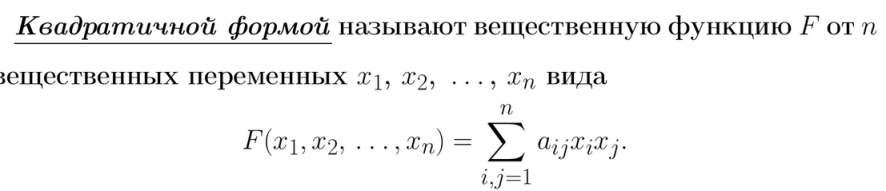
-
Положительно определенные квадратичные функции. Критерий Сильвестра.
Определение.
Квадратичная функция
на линейном
пространстве L
называется положительно определенной,
если
; отрицательно
определенной, если
.
-
Евклидовы пространства, условие изоморфизма.( не точно!)
Вещественное
линейное пространство ![]() называется евклидовым, если каждой
паре элементов
называется евклидовым, если каждой
паре элементов ![]() этого
пространства поставлено в соответствие
действительное число
этого
пространства поставлено в соответствие
действительное число![]() ,
называемое скалярным произведением,
причем это соответствие удовлетворяет
следующим условиям:
,
называемое скалярным произведением,
причем это соответствие удовлетворяет
следующим условиям:

Вещественное линейное пространство со скалярным произведением называется евклидовым пространством. Нормой элемента a ∈ V называется число p ν(a, a).
Изоморфизмом линейных пространств называется биективный линейный оператор. Два линейных пространства U и V называются изо- морфными, если существует изоморфизм из U в V .
-
Неравенство Коши-Буняковского. Модуль вектора, расстояние и косинус угла между векторами.
Неравенство
Коши–Буняковского.
![]()
Модулем
(длиной) вектора ![]() называется длина(норма)
соответствующего отрезка
называется длина(норма)
соответствующего отрезка ![]() и
обозначается как
и
обозначается как ![]() .
.
Для любых двух ненулевых векторов x и y евклидова пространства E со скалярным призведением (x, y) определен угол между векторами x и y:
![]()
Для любых двух ненулевых векторов x и y евклидова пространства E со скалярным призведением (x, y) определено расстояние между векторами x и y:
![]()
-
Процесс ортогонализации Грама-Шмидта
Пусть
![]() –
базис евклидова пространства V . Тогда
элементы
–
базис евклидова пространства V . Тогда
элементы

являются
ортогональным базисом V . Более того,
если
![]() –
система образующих V , то ненулевые
элементы набора
–
система образующих V , то ненулевые
элементы набора![]() образуют
базис пространства V .
образуют
базис пространства V .
-
Ортогональное дополнение к подпространству евклидова пространства.
Определение: Два подпространства и унитарного (евклидова) пространства наз-ся ортогональными , если : или
Вектор, ортогональный
к подпространству : Пусть
L – линейное подпространство евклидова
(унитарного) пространства
![]() .
Вектор x называется ортогональным к
подпространству L, если он ортогонален
каждому вектору из этого подпространства.
Обозначение:
.
Вектор x называется ортогональным к
подпространству L, если он ортогонален
каждому вектору из этого подпространства.
Обозначение:
![]() .
.
Ортогональное
дополнение к подпространству: Пусть
L – линейное подпространство евклидова
пространства
![]() .
Совокупность всех
векторов
.
Совокупность всех
векторов
![]() ,
ортогональных подпространству L,
называется ортогональным дополнением
к L. Обозначение:
,
ортогональных подпространству L,
называется ортогональным дополнением
к L. Обозначение:
![]() .
.
Т. об ортогональном дополнении как подпространстве : Ортогональное дополнение к подпространству является линейным подпространством того же пространства.
