10. Жорданова форма матрицы. Алгоритм нахождения Жордановой нормальной формы матрицы.

Жорданова форма. Матрица вида

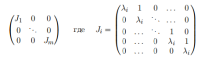
называется жордановой матрицей или жордановой формой матрицы оператора. Теорема. Для любого оператора, действующего в комплексном линейном пространстве, существует базис, в котором его матрица жорданова. Такой базис называется жордановым базисом оператора. Естественно, любая из клеток может иметь размер 1 × 1. Если все жордановы клетки имеют такой размер, то жорданова форма – это просто диагональная форма матрицы оператора.

Для нахождения жордановой формы квадратной матрицынужно выполнить следующие действия.

1. Составить характеристическую матрицу .

2. Найти ее инвариантные множители одним из способов

3. По инвариантным множителям составить таблицу элементарных делителей.

4. По элементарным делителям составить жорданову форму .

11. Сопряженное пространство, дуальные базисы, второе сопряженное пространство

Сопряженное пространство

Для линейных функционалов на линейном пространстве можно определить операции сложения и умножения на число:

• 

• 

Эти определения удовлетворяют аксиомам линейного пространства. То есть, совокупность всех линейных функционалов на также образует линейное пространство. Это пространство называетсясопряжённым к , оно обычно обозначается . В конечномерном случае сопряжённое пространство имеет ту же размерность что и пространство . Обычно элементы пространства обозначают вектором-строкой, а элементы — вектором-столбцом. В тензорном исчислении применяется обозначение для элементов (верхний, или контравариантный индекс) и для элементов (нижний, или ковариантный индекс).

Верно также что пространство, сопряжённое к сопряжённому , совпадает с .

Второе сопряженное пространство

ВТОРОЕ СОПРЯЖЕННОЕ ПРОСТРАНСТВО - пространство X'', сопряженное к пространству X', сопряженному к отделимому локально выпуклому пространству X, наделенному сильной топологией. Каждый элемент х ∈ Х порождает элемент F ∈ X'' по формуле F(f) = f(x) (f ∈ X'). Если X'' = X, то пространство X наз. рефлексивным. Если X - бочечное пространство, то линейное отображение π : x → F является изоморфным вложением пространства X в пространство X'', наделенное сильной топологией. Вложение π наз. каноническим. Для нормированных пространств π есть изометрическое вложение.

Дуальный базис

ДВОЙСТВЕННЫЙ БАЗИС, дуальный базис, к базису {е₁, ..., е_n} модуля Е относительно формы f - такой базис {c₁, ..., c_n} модуля Е, что

f(e_i, c_i) = 1, f(e_i, c_j) = 0, i ≠ j, 1 ≤ i, j ≥ n,

12. Билинейные функции и формы, изменение матрицы при переходе

к новому базису.

Пусть векторное пространство над полем .

Определение 1. Билинейной формой векторного пространства называется скалярная функция двух векторных аргументов со значениями в , линейная по каждому аргументу. Т. е. каждой паре ставится в соответствие число , удовлетворяющее условиям линейности: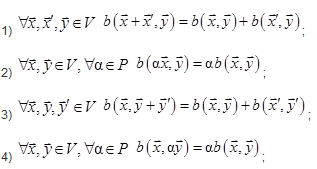

Координатную форму записи билинейной формы.

Матричная форма записи билинейной формы.

Где матрица, 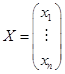это координатный столбец вектора , а 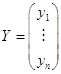это координатный столбец вектора .

Итак, каждой билинейной форме соответствует квадратная матрица, и обратное, каждой квадратной матрице соответствует билинейная форма в этом же базисе.

Изменение матрицы билинейной формы при изменении базиса.

Пусть заданы два базиса и , матрица перехода, матрица билинейной формы в старом базисе, — в новом, тогда

Определение 2. Билинейная форма называется Невырожденной, если ее матрица в некотором базисе, а значит и в любом, невырожденная.

Определение 3. Билинейная форма называется Симметричной Если .