1. Условие изоморфизма конечномерных линейных пространств

Два линейных пространства иназываютсяизоморфными, если между их элементами можно установить такое взаимно однозначное соответствие, что выполняются условия:

1) сумме векторов пространства соответствует сумма соответствующих векторов пространства

2) произведению числа на вектор пространства соответствует про изведение того же числа на соответствующий вектор пространства

Другими словами, изоморфизм — это взаимно однозначное соответствие, сохраняющее линейные операции

2. Матрица перехода к новому базису, изменение координат вектора.

Пусть векторы , ... ,  образуют базис пространства V, а векторы  , , ... ,   - другой базис этого пространства. Каждый вектор разлагается по базису , ... , . Запишем эти разложения в виде системы равенств

                                = + + ... + ,

                               = + + ... + ,

                                 ............................................

                               = + + ... +                         (2)

или, кратко,

                                                  = 

(суммирование по первому индексу коэффициентов ).

Коэффициенты разложений (2) образуют матрицу T перехода от базиса , ... ,  к базису  , , ... , .

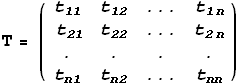
3. Формула для размерности суммы двух подпространств

Теорема о размерности суммы двух линейных подпространств (формула Грассмана). Если U и V – подпространства линейного пространства W, то

dim U + dim V = dim(U + V ) + dim(U ∩ V ).

Линейные подпространства, размерность линейной оболочки,

способы задания линейного подпространства

Множество K векторов из линейного пространства L называется линейным подпространством пространства L , если сумма x + y любых двух векторов x и y из L принадлежит K и произведение α·x любого числа α и любого вектора x и y из L принадлежит K:

Размерность линейной оболочки столбцов (строк) матрицы равна рангу матрицы.

Линейные подпространства могут быть заданы двумя способами: или однородной системой линейных уравнений илилинейной оболочной.

4. Прямая сумма подпространств, различные определения

Определение 1 Пространство V называется прямой суммой подпространств U и W, если каждый элемент v ∈ V мо жет быть единственным способом представлен в виде суммы v = u + w, где u ∈ U, а w ∈ W. Обозначение: V = U ⊕ W. Эквивалентная формули- ровка: V = U ⊕ W, если V = U + W и U ∩ V = ∅. Если V = U ⊕ W, то объединение базисов подпространств U и W есть базис пространства V .

Определение 2 Определение. Пусть и М – произвольные векторные подпространства векторного пространства . Сумма подпространств  называется прямой суммой, если , существует только одна пара векторов , такая, что .

5. Линейное отображение векторных пространств, ядро и образ.

Линейным отображением векторного пространства S в векторное пространство T называется функция α, определенная на S со значениями а T,удовлетворяющая требованию линейности

Ядром линейного отображения L : U → V называется множество всех тех элементов x пространства U, для которых L(x) = 0 (т. е. ядро линейного оператора – это пространство решений уравнения L(x) = 0). Обозначение: Ker L

Образом линейного отображения Образом линейного оператора L : U → V называется множество всех элементов y пространства V , представимых в виде y = L(x). Образ обозначается через Im L. Другими словами

Im L = {L(x)| x ∈ V }