Добавил:

okl5xcv667 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Нижегородский Государственный Технический Университет им. Р.Е. Алексеева

Предмет:

Сопротивление материалов

Файл:

РАЗДЕЛ 1

.pdf

Скачиваний:

Добавлен:

19.06.2017

Размер:

1.02 Mб

Скачать

☆

<<< < Предыдущая 12 / 22

Q y

Mx1

2qa

const

Mx2

1z2

/ 0a л.з

Mx2

Mx 0 0

0 0

Mx2 0

Mx1

Mx a 2qa 2

a a

III участок: 0 z3

-6qa 6qz

/ a л.

a z3

Mx3

/ a

Mx3 qa2 6qaz3

/ a

л.з.

6qz32

л.з.

0 0

п.з.

z3 / 0

Mx3

Mx3 0 1

0 a

a a

Mx3

Mx3 0

Mx3

Mx3 a

2qa

Т а б л и ц а 2

Вычисление элементов площади грузовой эпюры и ординат единичных эпюр

	Грузовое							I-е единичное							II-е единичное													III-е едини
состояние								состояние								состояние												состояние
ω1	1	2qa2			a qa3			1	2		a			a				1	2		a		a						1		2a			a

	2							2	3
	2							2	3			3				2 3						3							2a 3 3
																1				a		4a
	1							1	2				a				a									1					a			4		2
																	a
ω2				2			3									2				3		6
		2qa			a qa						a																	a
	2	2qa			a qa			2	3		a	3				2a												a
	2							2	3			3				2a										2a					3			6 3
																3
ω3			6qa3			qa3		1		a		a				1					a			3a				1					a		3
																	a													a
		12				2											a				2				4					a		2			4
		12				2		2 2 4								2					2				4		2a					2			4

Лист

КР-СМ-НГТУ-12КС3-012-14

Изм. Лист

№ докум.

Подпись Дата

ω4							1			qa2 a
ω4										qa2 a																	1			1									a							1							2a							5a							1				2a		5
			2																								1			1									a							1							2a							5a							1				2a		5
	qa3																															a																a																					a
	qa3																										2 3												6							2							3							6							2a				3		6
		2
		2
				ω5 qa3																												0																1				a						a												0
				ω5 qa3																												0																1																						0
																																																				2					2
B			qa4										1			1			1			1				1		1							17qa4
yC								1							1																										;
yC			EJ x					1							1																										;
			EJ x										3			3 2 4 2 6																			24EJ x
B			qa4							1				1	1			2			1			3			1			5						1			1				11qa	4
yD																																														;
yD			EJ x																																								24EJ x			;
			EJ x											3				3 2 4 2 6																					2				24EJ x
B				qa3									1	1		2			1				3			1			5									23qa		3
QB									1																																	.
QB				EJ x					1																																	.
				EJ x									3				3 2 4 2 6																				24EJ x
7) Из условия прочности и жесткости подберем размер поперечного сечения
Условие прочности при изгибе:																																																Условие жесткости при изгибе:
					М max									;																														D							a				;
								x						;																														D											;
																																																	200
						Wx																																											200
					М xmax								2qa 2 ;																																		11qa 4										a		;
												bh		2		b 2b				2					4b		3				2b			3													24EJ x										200		;
				Wx								bh				b 2b									4b						2b							;											bh			3								3			8b	4		2b		4
				Wx																						6						3						;														3								3				4				4
													6					6								6						3													J x											b 2b													;
																																																	12								12					12				3
					2qa					2		3			T					3					3qa			2	nT
										2																		2

															nT ; b																		;												11qa3 3												1
						2b3																					T						;												11qa3 3												1		;
						2b3																					T																		24E 2b4												200		;
				b 3							3 0,015 (0,8)2 1,5																																		24E 2b4												200

																											;																	b 4						33qa3 200											; b	4			33 0,015(0,8)3							200		;
																240											;																							33qa3 200															33 0,015(0,8)3							200
																240																																						48E													48 2,1105
				b 0,0565м;																																																		48E													48 2,1105
				b 0,0565м;																																								b 0,05001м
				b 0,057м.																																								b 0,05001м
				b 0,057м.																																								b 0,051м
																																												b 0,051м

8) Сравнивая результаты расчетов на прочность и жесткость, выбираем больший из полученных размеров, как удовлетворяющий обоим условиям: b=0,057 м.

Лист

КР-СМ-НГТУ-12КС3-012-14

Изм. Лист

№ докум.

Подпись Дата

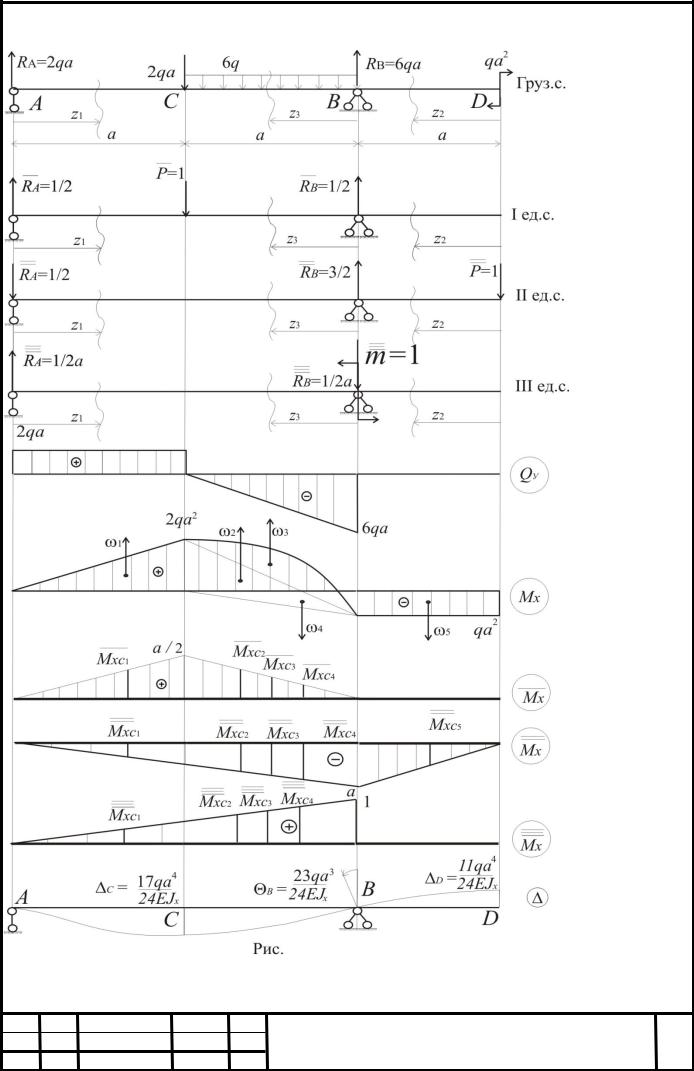
Рисунок 3. К расчету изгиба статически определимого бруса

Лист

КР-СМ-НГТУ-12КС3-012-14

Изм. Лист

№ докум.

Подпись Дата

1.3 Расчет плоской статически определимой рамы. 1.3.1 Условие задачи.

Для плоской рамы (схема 36) постоянной жесткости, выполненной из стали 35ХГСА и имеющей кольцевое сечение (D/d = 2), из условий прочности и жесткости сечения D ( A a / 200 ) определить размеры кольцевого сечения.

1.3.2 Краткие теоретические сведения При воздействии на плоскую раму силовой нагрузкой поперечные

сечения стержней рамы получают продольные (вдоль рассматриваемого стержня), поперечные (перпендикулярно оси рассматриваемого стержня) и угловые (угол поворота рассматриваемого сечения) перемещения, которые определяются методом Мора, интеграл которого должен содержать три слагаемых:

перемещение, обусловленное действием продольных сил в стержнях рамы;

перемещение, обусловленное действием поперечных сил в стержнях рамы;

перемещение, обусловленное действием изгибающих моментов в стержнях рамы;

Однако эксплуатационная практика и расчеты показывают, что доминирующими перемещениями, являются перемещения, обусловленные изгибающим моментом, а перемещения вызванные действием продольных и поперечных сил можно пренебречь. Таким образом, интеграл Мора для определения перемещений сечений рамы принимает вид


	M x M x	ds ,

	EJ x
S

где M x и M x ‒ изгибающие моменты в исходном (грузовом) и единичном

состояниях;

EJ x ‒ жесткость стержней рамы на изгиб;

S‒ контур рамы.

1.3.3 Решение задачи (рис. 4).

1) Определяем опорные реакции для грузового состояния из условия равновесия

momA 0 RD qa2 ; momB 0 RAy qa2 ; X 0 RAx qa.

Проверка: Y 0.

2)Строим эпюру изгибающих моментов в грузовом состоянии (рис. 4);

3)Снимаем с рамы заданную нагрузку и в сеченииD, перемещение которого

ищется, прикладываем единичную силу P 1 (единичное состояние)в

Лист

КР-СМ-НГТУ-12КС3-012-14

Изм. Лист

№ докум.

Подпись Дата

горизонтальном направлении, т.к. в вертикальном направлении перемещение сечения Dравно нулю согласно опоре.

4)Определяем опорные реакции в единичном состоянии

momA 0 RD 1; momB 0 RAy 1; X 0 RAx 1.

Проверка: Y 0.

5)Строим эпюры изгибающих моментов в единичном состоянии (рис. 4).

6)Определяем горизонтальное перемещение сечения Dметодом Мора, вычисляя интеграл Мора по правилу Верещагина. Для сокращения записи будем считать, что ω‒ площадь грузовой эпюры Mx.

										qa2					a				qa3										1		2		a					2	a
										qa2																M xc

											2
							1				2																1			3								3
							1				2									4										3								3
											2									4
							2					qa3																	1			a					a
												qa3														M xc2						a					a


											12																			2						2
												qa2																						2								2
																	a					qa3				M xc3 1									a								a
							3						2
													2																					3							3
																2						4												3							3
																2						4
									3														qa			3				qa3										qa3
		M	x	M xc					3					M xc								1	qa			3	2			qa3						a				qa3				2
D			x			ds						i						i										a																	a
D			EJ x			ds						EJ x									EJ x							a																	a
	S		EJ x						i 1			EJ x									EJ x				4 3					12						2					4 3
	S								i 1								i
qa4 1			1		1				7		qa4					0,292						qa4		.
																0,292								.
			24					24 EJ x														EJ x
EJ x 6			24		6			24 EJ x														EJ x

7) Определяем размер кольцевого сечения из условия жесткости

D 0,292 qa4 D ,

EJ x

где D 200a 5 мм ‒допускаемое перемещение сечения D, обусловленное

эксплуатационными условиями рамы.

Отсюда находим сначала необходимый момент инерции поперечного сечения

0,292qa4

0,292 0,002

14 м

55,62 10 8 м4 55,62 см4 .

E D

2,1 10

5 MH

5 10

Лист

КР-СМ-НГТУ-12КС3-012-14

Изм. Лист

№ докум.

Подпись Дата

Теперь, зная, что

		D	4		d		4	D	4	1 0,5 4 D	4	0,9375 55,62 10 8 м4 ,
J				1	d			D
J	x			1
	x	64						64		64
		64				D		64		64

определяем необходимый размер внешнего диаметра из условия жесткости

D 4

64 55,62 10 8 м4

10 2 м 5,897 10 2

м 0,059 м 59 мм.

1209 ,2

0,9375

8) Определяем размер кольцевого сечения из условия прочности

max

M xmax

где M xmax

qa2

‒ изгибающий момент в опасном сечении рамы;

1400

933 МПа ‒допускаемые напряжения;

nт

1,5

= 1400 МПа ‒ предел текучести стали 35ХГСА;

nт 1,5 ‒ коэффициент запаса по пределу текучести.

Отсюда находим сначала необходимый момент сопротивления поперечного сечения

			M xmax					qa2		0,002			МН		12 м2
			M xmax					2		0,002			м		12 м2				6		3		3
	Wx																1,072 10			м		1,072 см		.
	Wx										2 933			МН			1,072 10			м		1,072 см		.
														МН
															м2
															м2
Теперь, зная, что для кольцевого сечения
		D		3		d			4	D	3	1 0,5 4				D		3	1,072 10 6 м3 ,
W					1	d				D						D		0,9375
W	x				1													0,9375
	x	32								32						32
		32					D			32						32

определяем необходимый размер внешнего диаметра из условия прочности

D 3 32 1,072 10 6 м3 3 11,647 10 2 м 2,267 10 2 м 2,3 см =23 мм.

0,9375

Из двух размеров (59 мм и 23 мм) выбираем наибольший и принимаем D=59 мм, как удовлетворяющий обоим условиям ‒ условию прочности и условию жесткости.

Лист

КР-СМ-НГТУ-12КС3-012-14

Изм. Лист

№ докум.

Подпись Дата

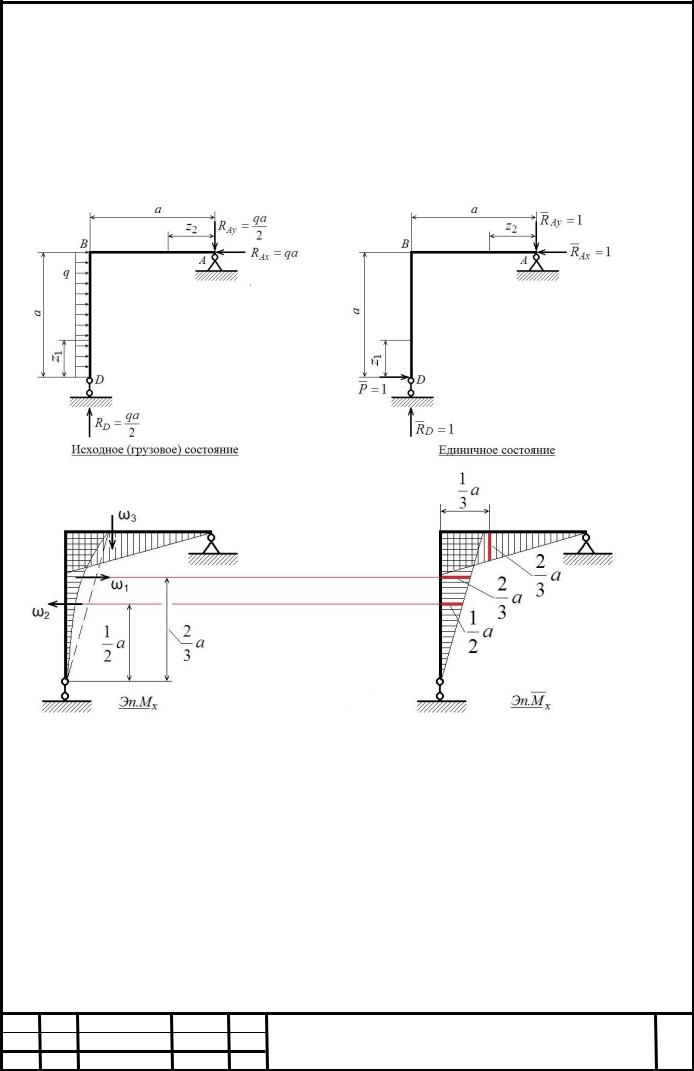
Рисунок 4. К расчету статически определимой рамы

Лист

КР-СМ-НГТУ-12КС3-012-14

Изм. Лист

№ докум.

Подпись Дата

1.5. Расчет статически определимой рамы при сложном нагружении. 1.5.1. Условие задачи.

Для плоско-пространственной рамы (схема 15), выполненной из стальных брусьев (Ст.3) круглого поперечного сечения диаметром d, из условия прочности определить d и при найденном значении вычислить вертикальное перемещение сечения A. (при расчете принять G=0,4E).

1.5.2. Краткие теоретические сведения.

При сложном нагружении пространственной рамы в поперечных сечениях стержней в общем случае возникают все шесть внутренних усилий, однако основными усилиями, влияющими на деформированный вид рамы, являются изгибающие Мх, Муи крутящий Мz моменты. Поэтому интеграл Мора будет содержать три слагаемых

M x M x

M y M y

M z M z

ds .

EJ x

EJ y

EJk

1.5.3. Решение задачи (рис.5).

1) Строим эпюры и аналитические выражения изгибающего и крутящего моментов в грузовом и единичном состояниях. Так как рама плоскопространственная, лежащая в горизонтальной плоскости, и нагрузка действует только в вертикальной плоскости, то в поперечных сечениях стержней рамы возникнут только Mx и Mz, а Му на всех участках равен нулю.

Грузовое состояние

Участок 1

M x qa2

M z1 0;

Участок 2

M x2 qa z2

M z2 qa2

Единичное состояние

Участок 1

M x

1 z

M z

Участок 2

1 z

1 a;

M x

M z

Опасным будет сечение в заделке, где M x qa2

и M z qa2 .

2) Определяем диаметр стержней рамы из условия прочности.

Так как в опасном сечении стержень испытывает одновременно изгиб и кручение, а материал рамы относится к пластичным, по используем гипотезу наибольших касательных напряжений, согласно которой

экв. 2z 4 2 ,

где т 240 160 МПа ‒ допускаемые напряжения; nт 1,5

т 240 МПа ‒ предел текучести стали Ст.3;

d 3

В результате условие прочности принимает вид

Лист

КР-СМ-НГТУ-12КС3-012-14

Изм. Лист

№ докум.

Подпись Дата

экв.

M x2 M z2

Отсюда находим необходимый по условию прочности диаметр стержней рамы

3 32 2qa

32 1,414 0,002 MH

12 м2

d 3

M x M z

3 0,180 10 3 м

160

МН

м2

0,565 10 1 м 0,0565

м 56,5 мм.

Принимаем d=56,5 мм.

3) Определяем в общем виде вертикальное перемещение сеченияА,

вычисляя интеграл Мора по правилу Верещагина.

M x

M z

qa2 a

EJ x

EJ k

EJ x

qa2

a a

qa4 1

2,917 qa4 .

0,4 EJ k

0,4 2

EJ x

Знак минус говорит о том, что сечение А переместилось в сторону,

противоположную единичной силе, т.е. в верх. Здесь учтено, что

d 4

(56,5)410 12

м4 500223 ,0 10 12 м4 5 10 7 108

см4 50 см4 ;

J k

d 4

2J x .

4) Вычисляем перемещение сечения А при найденном диаметре

стержней рамы

МН

2,917

qa4

2,917

0,002

14 м4

EJ x

5 МН

2,1 10

50 10

м2

5,556 10 5 103 м 0,0556

м 55,6 мм.

Лист

Изм. Лист

№ докум.

Подпись Дата

КР-СМ-НГТУ-12КС3-012-14

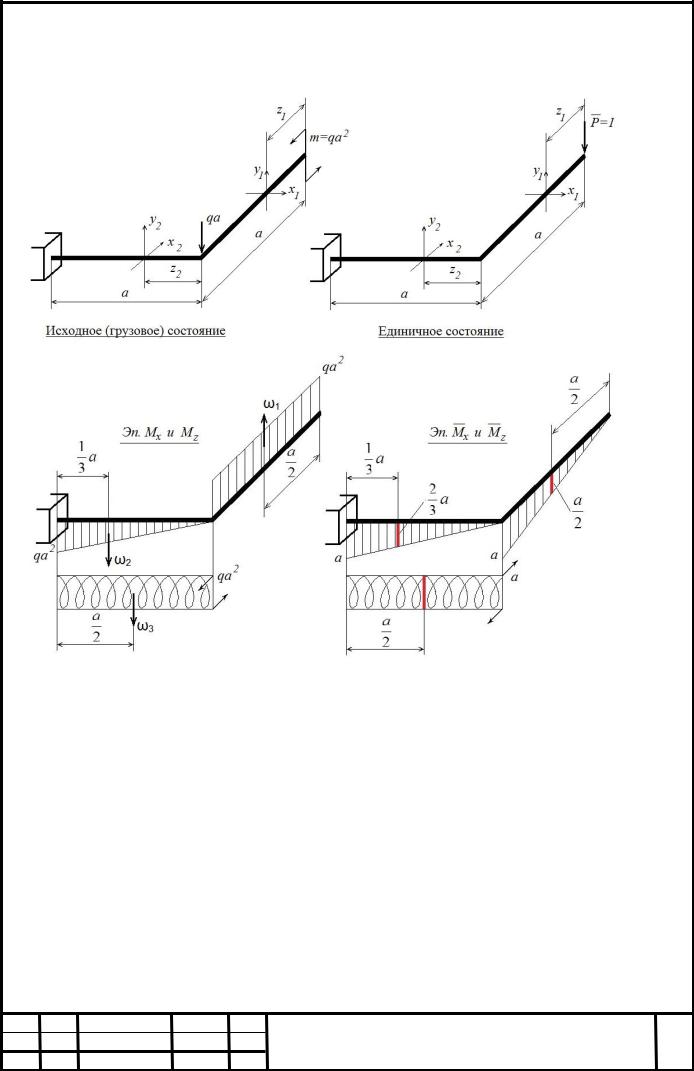
Рисунок 5. К расчету плоско-пространственной рамы

Лист

КР-СМ-НГТУ-12КС3-012-14

Изм. Лист

№ докум.

Подпись Дата

<<< < Предыдущая 12 / 22

Соседние файлы в предмете Сопротивление материалов

#
19.06.2017361.37 Кб6Введение, понятия, обозначения.pdf
#
19.06.2017345.2 Кб3ЗАДАНИЕ, ШИЛЬДИК, ТИТ.ЛИСТ.pdf
#
19.06.2017177.36 Кб6ЗАКЛЮЧЕНИЕ, Литература.pdf
#
19.06.20172.27 Mб3ПРИЛОЖЕНИЯ.pdf
#
19.06.20171.02 Mб7РАЗДЕЛ 1.pdf
#
19.06.2017706.45 Кб6РАЗДЕЛ 2.pdf
#
19.06.2017312.37 Кб3РАЗДЕЛ 3.pdf
#
19.06.2017377.52 Кб4РАЗДЕЛ 4.pdf