
РАЗДЕЛ 2
.pdf
2. Расчет на прочность и жесткость статически неопределимых элементов конструкций
Задание № 12
Выполнил: студент гр. 12-КС-3 Иванов И.И.
Принял: к.т.н., доцент Сидоров А.А.
Номер схемы |
42 |
43 |
47 |
Средний балл |
Оценка |
|
|
|
|
|
|
|
|
|
Подпись |
|
|
|
|
|
|
|
|
|
Нижний Новгород 2015
Лист
КР-СМ-НГТУ-12КС3-012-14
Изм. Лист |
№ докум. |
Подпись Дата |

2.1. Расчет статически неопределимой рамы на прочность. 2.1.1.Условие задачи
Для стальной (Ст.3) рамы (схема 47), имеющей одинаковое квадратное поперечное сечение на всех участках из условия прочности определить размер квадратного поперечного сечения.
2.1.2. Краткие теоретические сведения.
Статически неопределимой системой (конструкцией) называется геометрически неизменяемая система, в которой для определения внутренних усилий в элементах и реакций опор недостаточно одних лишь уравнений статики. Для раскрытия статической неопределимости применяется метод сил, согласно которому выбирается основная система, формируется эквивалентная система и из условия совместности деформаций составляются канонические уравнения
метода сил
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
ip ij X j 0 |
(i, j 1,2,..., n) , |
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
где n –степень статической неопределимости; |
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||
ip |
M xp M xi |
ds - перемещение в точке приложения и в направлении i-го |
|||||||||||
|
|
|
|
||||||||||
|
|
|
|
S |
|
EJ x |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
неизвестного от действия внешней нагрузки в основной системе; |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EJ |
|
|
|
|
|
|
|||
|
|
|
|
M xi M xj |
ds |
- перемещение в точке приложения и в направлении i- |
|||||||
ij |
|
|
|||||||||||
|
|
|
S |
|
|
|
|
x |
|
|
|
||
гонеизвестного от действия единичного усилия, приложенного в точке приложения и в направлении j-го неизвестного ( X j 1) в основной системе;
S - контур рамы;
Е – модуль упругости материала;
J x - момент инерции поперечного сечения;
M xp - изгибающий момент в основной системе от действия внешней нагрузки
(грузовое состояние);
M xi - изгибающий момент в основной системе от действия единичного усилия, приложенного в точке приложения и в направлении i-го неизвестного Xi 1 (i-
единичное состояние);
X1, X2 , ..., Xi , ..., Xn - неизвестные усилия в эквивалентной системе.
2.1.3. Решение задачи (рис. 6÷10).
1)Определяем степень статической неопределимости.
Данную раму удобнее рассматривать как внешне статически неопределимую. Так как к раме приложено пять опорных усилий, а в плоскости рамы можно составить только три уравнения равновесия, то степень статической неопределимости n=5-3=2.
Лист
КР-СМ-НГТУ-12КС3-012-14
Изм. Лист |
№ докум. |
Подпись Дата |
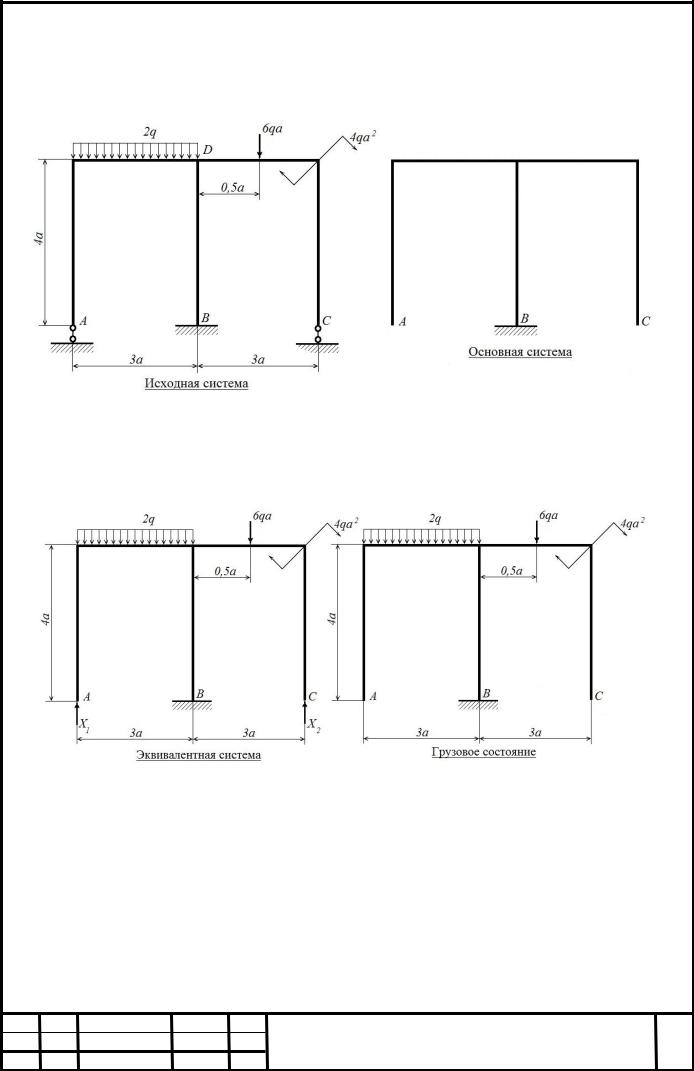
2) Из нескольких, возможных основных систем выбираем ту, с которой удобнее работать с точки зрения объема вычислений (рис. 6).
Рисунок 6. Исходная и основная системы рамы
3) Изображаем эквивалентную систему, загружая основную систему внешней нагрузкой и неизвестными опорными усилиями X1, X 2 (рис. 7).
Рисунок 7. Эквивалентная система и грузовое состояние рамы
4) Строим эпюры изгибающих моментов в грузовом и единичных состояниях (рис. 8 и 9)
Лист
КР-СМ-НГТУ-12КС3-012-14
Изм. Лист |
№ докум. |
Подпись Дата |
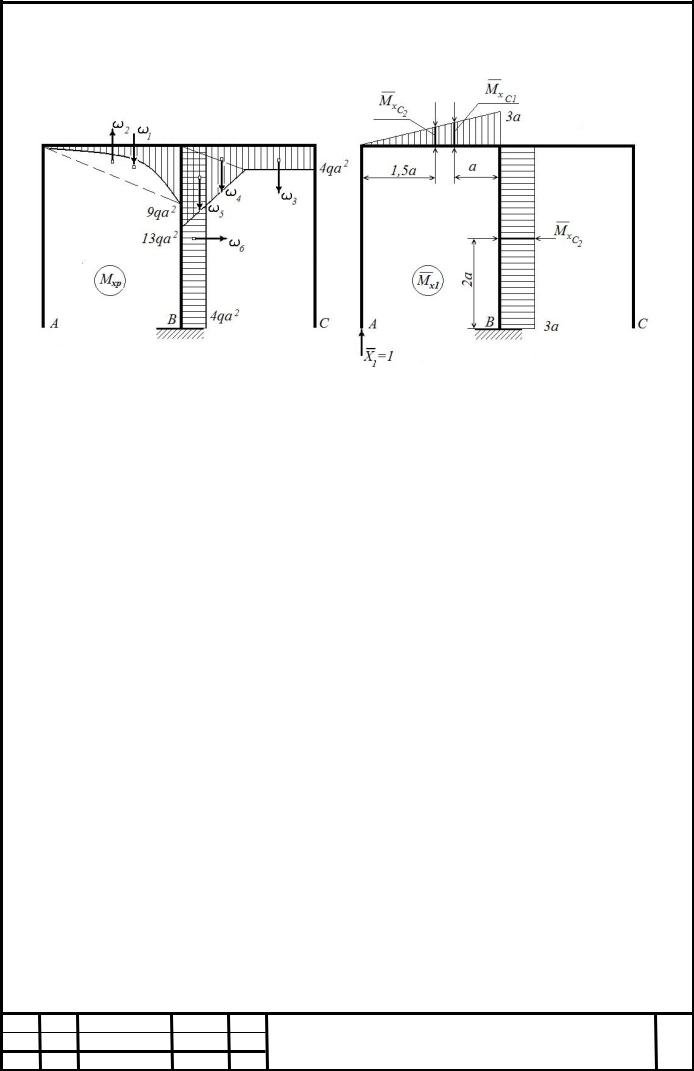
Рисунок 8. Эпюры изгибающих моментов в грузовом и первом единичном состояниях
5) Подсчитываем коэффициенты канонических уравнений методом Мора, вычисляя интегралы по способу Верещагина.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9qa2 |
3a |
|
|
|
|
|
|
|
|
|
|
|
2q (3a)3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
111 qa4 |
|
|
|
|
|
|
|
qa4 |
|
|
|
|||||||||||||||||||||||||
1 p |
|
M xp M x1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
ds |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3a |
|
|
|
|
|
|
|
|
|
a |
4qa |
|
|
|
4a 3a |
|
|
|
|
|
|
27,750 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
EJ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 EJ x |
EJ x |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
S |
|
|
|
|
|
|
|
|
|
EJ x |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
12 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3a 3a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
11 |
|
|
M |
x1 |
M |
x1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qa3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
ds |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3a 4a 3a 3a 45 |
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
EJ x |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
EJ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
EJ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
12 |
M x1 M x2 |
ds |
|
1 |
|
|
|
4a 3a 3a 36 |
|
; |
|
21 12 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
EJ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
S |
|
EJ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
EJ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4qa2 |
|
3 |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
13qa2 |
3a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
M xp |
M x1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3a |
|
|
|
1 |
|
3 |
|
|
|
|
|
3a |
|
|
|
|
1 |
|
3a |
|
|
|
3a |
|
2 |
|
|
|
3a |
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
2 p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
ds |
|
|
|
|
|
|
|
[ 4qa |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
EJ x |
|
|
|
EJ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2 2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
2 3 2 |
|
|
|
2 |
|
|
|
|
2 3 2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
4qa2 |
4a 3a] |
|
663 |
|
|
qa4 |
82,875 |
qa4 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
EJ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EJ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
22 |
M |
x2 |
M |
x2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
3a 3a |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
qa3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
ds |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3a |
4a 3a 3a |
|
45 |
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
EJ x |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
EJ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
S |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EJ x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Лист
КР-СМ-НГТУ-12КС3-012-14
Изм. Лист |
№ докум. |
Подпись Дата |

6)Определяем опорные реакции X1 и X 2 . Для этого подставляем найденные коэффициента в систему канонических уравнений. После сокращения на общий
|
qa3 |
|
|
|
|
|
|
|
|
|
множитель |
|
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
EJ x |
|
|
|
|
|
|
|
|
|
|
|
|
27,750qa2 |
45 X |
1 |
36 X |
2 |
0 |
|
|
|
|
|
|
|
|
|
|
. |
||
|
|
|
|
36 X |
|
|
45 X |
|
0 |
|
|
|
82,875qa2 |
1 |
2 |
|
|||||
|
|
|
|
|
|
|
|
|||
Решение этих уравнений дает X1 2,379qa, |
|
X2 3,745qa . |
||||||||
В обоих случаях получили знак плюс, значит направление реакций совпадает с ранее выбранным.
7) Изображаем эквивалентную систему при найденных опорных реакциях и для нее строим эпюру изгибающих моментов как для обычной статически определимой рамы, загруженной заданной внешней нагрузкой и известными теперь уже силами X1 2,379 qa и X2 3,745 qa (рис. 9 и 10).
Рисунок 9. Второе единичное состояние и эквивалентная система рамы при найденных опорных реакциях
Лист
КР-СМ-НГТУ-12КС3-012-14
Изм. Лист |
№ докум. |
Подпись Дата |
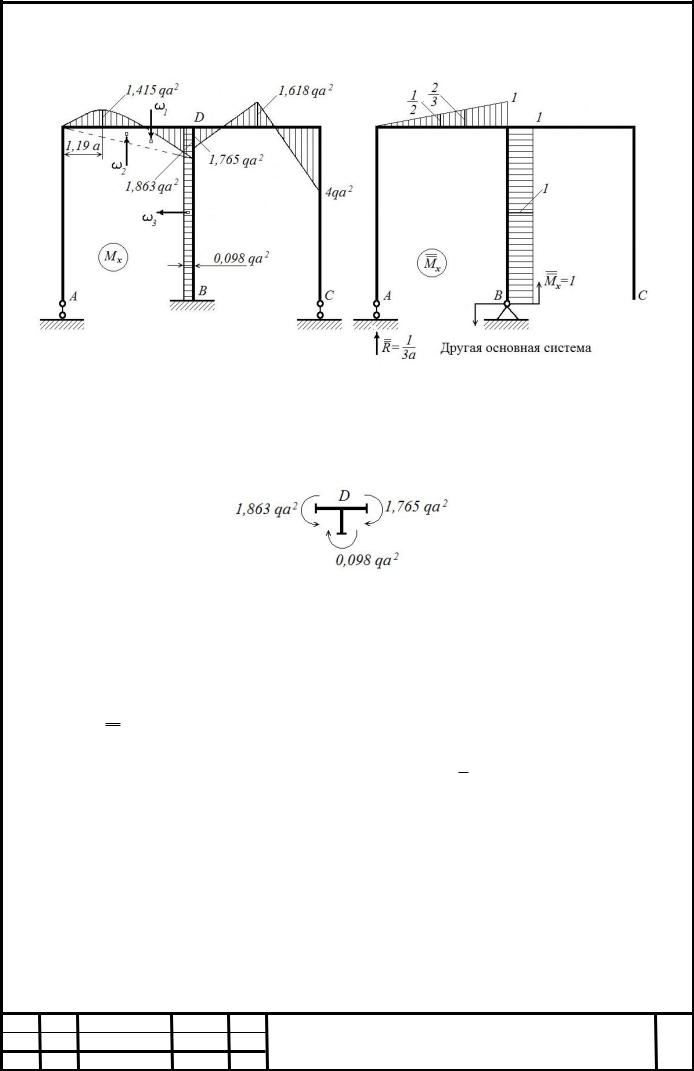
Рисунок 10. Эпюра изгибающих моментов в эквивалентной (исходной) системе и единичное состояние для деформационной проверки
8) Статическая проверка.
Вырежем узел D (рис. 10) и рассмотрим его равновесие по моменту
momD 0 1,863qa2 1,765qa2 0,098qa2 qa2 (1,863 1,863) 0 .
Условие равновесия узла удовлетворяется. 9) Деформационная проверка.
Проверку правильности построения эпюры изгибающего момента M x
делаем из условия, что угол поворота сеченияВв заделке равен нулю. Для этого выбираем другую основную систему и для нее строим эпюру изгибающих
моментов M x .
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
Bугл |
M |
x |
M |
x |
|
1,863qa2 3a |
|
2 |
|
2q (3a)3 |
|||||||||||
|
|
|
|
ds |
|
|
|
|
|
|
|
|
|
|
|||||||
|
EJ x |
|
|
|
|
|
|
|
|
||||||||||||
|
|
S |
|
|
|
|
EJ x |
2 |
|
|
3 |
|
12 |
||||||||
|
qa3 |
1,863 2,250 0,392 |
qa3 |
2,250 2,255 0. |
|||||||||||||||||
|
|
|
|||||||||||||||||||
|
EJ x |
|
|
|
|
|
|
|
|
|
|
|
|
EJ x |
|
|
|
|
|
||
Оценим погрешность в процентах: |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2,255 2,250 |
100% 0,2% |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2,250 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 0,098qa2 4a 1 2
,
что вполне удовлетворительно.
10) Определение поперечного сечения участков рамы.
Размеры квадратного поперечного сечения рамы находим из условия прочности
Лист
КР-СМ-НГТУ-12КС3-012-14
Изм. Лист |
№ докум. |
Подпись Дата |

zmax |
M xmax |
, |
|
Wx |
|||
|
|
где M xmax 4qa2 - изгибающий момент в опасном сечении рамы;
Wx b3 - момент сопротивления поперечного сечения стержней рамы при изгибе;
6
b– размер квадратного поперечного сечения;
т 240 = 160 МПа - допускаемые напряжения; nт 1,5
т 240 МПа - предел текучести стали Ст.3 (ГОСТ 380-2005, Сталь углеродистая обыкновенного качества);
nт =1,5 –коэффициент запаса по пределу текучести при статических нагрузках.
Из условия прочности определяем размер квадратного поперечного сечения стержней рамы
|
6M max |
|
|
6 4 0,002 (2)2 |
|
|
|
||
b 3 |
|
3 |
0,0012 0,106 м = 106 мм. |
||||||
x |
|
|
|
|
3 |
||||
|
|
|
|
|
160 |
|
|
|
|
Принимаем b=106 мм.
2.2.Расчет статически неопределимого бруса переменного сечения,
испытывающего кручение, на прочность. 2.2.1. Условие задачи.
Из условия прочности при кручении определить параметрd бруса переменного поперечного сечения (схема 42), выполненного из стали 35ХГСА.
2.2.2. Решение задачи (рис. 11).
1)Определяем степень статической неопределимости. К брусу приложены внешние моменты относительно его продольной оси, поэтому можно составить только одно уравнение равновесия. Неизвестных опорных моментов будет два. В результате n=2-1=1.
2)Из двух возможных выбираем основную систему, снимая внешнюю нагрузку и отбрасывая, например, правую опору.
3)Изображаем эквивалентную систему, загружая основную систему внешней нагрузкой и неизвестным опорным моментом X (рис.11).
4)Составляем для эквивалентной системы каноническое уравнение метода сил из условия, что угол поворота правого опорного сечения относительно продольной оси (угол закручивания) равен нулю
Лист
КР-СМ-НГТУ-12КС3-012-14
Изм. Лист |
№ докум. |
Подпись Дата |

1p 11 X 0 ,
где 1p ‒ угол поворота (закручивания) правого опорного сечения в эквивалентной системе от действия внешней нагрузки;
11 ‒ угол поворота (закручивания) правого опорного сечения в эквивалентной системе от действия единичного момента, приложенного вместо правого опорного момента X1 ;
G |
E |
|
2,1 105 МПа |
0,8 105 МПа ‒ модуль упругости стали 35ХГСА |
|
2(1 ) |
2(1 0,3) |
||||
|
|
|
при сдвиге;
5)Для вычисления коэффициентов канонического уравнения строим эпюры крутящих моментов в грузовом и единичном состояниях (рис. 11).
6)Так как брус переменного сечения, то подсчитываем моменты инерции при кручении бруса, выражая их через диаметр d для участка со сплошным сечением.
J k |
|
|
d 4 |
‒ момент инерции при кручении поперечного сечения первого |
|||||||||||||||||
1 |
|
32 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
участка; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
d |
4 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
d 4 |
|
|
|
|
|
d 4 |
1 |
|
15 d 4 |
15 |
|
|||||||
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||
J k |
|
|
|
|
|
|
|
|
|
|
|
(1 |
|
|
) |
|
|
|
|
|
J k ‒ момент инерции при |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 |
|
32 |
|
|
32 |
|
|
|
32 |
16 |
|
16 |
32 |
16 |
1 |
|||||
|
|
|
|
|
|
|
|
|
|
||||||||||||
кручении поперечного сечения второго участка; |
|||||||||||||||||||||
J k |
|
|
(2d )4 |
16 |
d 4 |
16J k |
|
‒ момент инерции при кручении поперечного |
|||||||||||||
3 |
|
|
|
|
|
|
|||||||||||||||
|
|
32 |
|
|
|
|
|
|
32 |
1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
сечения третьего участка.
7)Подсчитываем коэффициенты канонического уравнения, вычисляя интегралы Мора по правилу Верещагина.
|
l |
|
|
|
|
|
0,2a M |
|
|
|
|
|
0,3a M |
|
|
|
|
|
|
|
|
|
|
0,2a M |
|
|
|
|
|
|
|
|
|||
|
M |
zp |
M z |
|
zp |
M z |
|
|
zp |
|
M z |
2 |
|
|
|
zp |
M z |
3 |
|
|
|
||||||||||||||
1p |
|
|
|
|
dz |
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
1 |
|
|
dz1 |
|
|
|
|
|
|
|
|
|
dz2 |
|
|
3 |
|
|
|
|
|
dz3 |
||||||
|
GJ k (z) |
|
GJ k |
|
GJ k |
2 |
|
|
|
|
GJ k |
3 |
|
|
|
||||||||||||||||||||
|
0 |
|
|
|
|
|
0 |
|
|
1 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||
Лист
КР-СМ-НГТУ-12КС3-012-14
Изм. Лист |
№ докум. |
Подпись Дата |

0 0,2a ( 1) |
|
8qa2 |
0,3a ( 1) |
|
24qa2 0,2a ( 1) |
|
qa3 |
|||
|
|
|
|
|
|
|
|
|
|
(2,560 0,300) |
|
|
15 |
|
G 16J k1 |
|
|||||
GJ k1 |
|
G |
J k |
|
|
GJ k1 |
||||
|
|
|
|
|
||||||
|
|
|
16 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2,860 |
|
qa3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
GJ k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
0,2a |
|
|
|
|
|
|
0,3a |
|
|
|
|
|
|
|
|
|
0,2a |
|
z |
|
|
|
|
|
|
||||||
|
|
M z M z |
|
|
|
|
M |
z |
M z |
|
M |
z |
2 |
M z |
2 |
|
|
|
M |
3 |
M z |
3 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
dz |
|
|
1 |
|
1 |
dz |
|
|
|
|
|
|
|
dz |
|
|
|
|
|
|
|
|
dz |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||
11 |
|
|
GJ k ( z) |
|
|
|
|
|
|
1 |
|
GJ k |
|
|
|
|
|
GJ k |
|
|
3 |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
GJ k |
|
2 |
|
|
|
|
|
3 |
|
|
|
|
||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
1 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||
|
1 0,2a 1 |
|
1 0,3a 1 |
|
1 0,2a 1 |
|
|
a |
(0,2000 0,3200 0,0125 ) 0,5325 |
a |
. |
|||||
|
|
15 |
|
G 16 J k1 |
|
|
|
|||||||||
|
GJ k1 |
G |
J k |
|
|
GJ k1 |
|
|
|
GJ k1 |
||||||
|
|
|
|
|
|
|||||||||||
|
|
|
16 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Записываем каноническое уравнение при вычисленных коэффициентах |
||||||||||||||||
|
|
|
|
|
|
|
2,850 |
|
qa3 |
0,5325 |
a |
X 0 . |
|
|
||
|
|
|
|
|
|
|
GJ k |
GJ k |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
Отсюда находим правый опорный момент
X 0,53252,8500 qa2 5,3521qa2 .
Знак плюс говорит о том, что направление опорного момента выбрано правильно.
8)Изображаем эквивалентную систему при найденном опорном моменте и для нее строим искомую эпюру крутящих моментов по длине бруса (рис. ).
Делаем деформационную проверку из условия, что угол закручивания на левой опоре равен нулю. Для этого выбираем другую основную систему, отбрасывая левую опору, загружаем ее единичным моментом
Лист
КР-СМ-НГТУ-12КС3-012-14
Изм. Лист |
№ докум. |
Подпись Дата |

|
|
1) m 1и строим эпюру крутящих моментов в дополнительном единичном |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
состоянии. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
l |
M |
z |
M z |
|
|
0,2a M z |
M z1 |
|
|
|
0,3a M z |
2 |
M z2 |
|
0,2a M z |
3 |
M z3 |
|
|
|||||||||||||
|
|
|
|
A |
|
|
|
|
|
dz |
|
|
|
|
1 |
|
|
dz1 |
|
|
|
|
|
|
|
dz1 |
|
|
|
|
|
dz3 |
|
||||||||
|
|
|
|
GJ k (z) |
|
|
GJ k |
|
GJ k |
|
|
|
GJ k |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
1 |
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|||
|
|
|
|
5,3521qa2 0,2a 1 |
|
2,648qa2 0,3a 1 |
|
18,648qa2 0,2a 1 |
|
qa3 |
( 1,0704 |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 J k |
|
|
|
|
|
G 16J k1 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
GJ k1 |
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
GJ k1 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,8474 0,2331) |
qa3 |
( 1,0704 |
1,0805) 0 . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
GJ k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оценим погрешность в процентах: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,0805 1,0704 |
100% 0,9% , |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,0704 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
что вполне удовлетворительно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
2) Определяем диаметр dиз условия прочности для всего бруса. |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
Так как брус имеет переменное (ступенчатое) поперечное сечение и на каждом |
|||||||||||||||||||||||||||||||||||||||
|
|
участке действует свой крутящий момент, то необходимо составить условие |
|||||||||||||||||||||||||||||||||||||||
|
|
прочности для каждого участка. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
Участок 1: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Wz |
|
d 3 |
‒ момент сопротивления бруса кручению на 1-ом участке; |
|
|||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
M z |
5,352qa2 ‒ крутящий момент на 1-ом участке; |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ ] |
|
т |
1400 |
933 МПа ‒ допускаемые напряжения для стали 35ХГСА; |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
nт |
|
1,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
max |
|
M z |
|
d 3 |
16M z |
3 |
16 5,352qa2 |
|
|
85,632 0,002 |
МН |
12 м2 |
|
|||||||||||||||||||||||||
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
м |
|
||||||||||||||||||
|
|
|
1 |
|
|
|
|
Wz1 |
|
|
|
|
|
|
|
|
[ ] |
|
|
|
|
[ ] |
|
|
|
|
|
3,14 933 МН |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
м2 |
|
|
|
|
|
3 5,846 10 5 м3 |
0,0388 |
м 38,8 мм . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
Участок 2: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
15 |
|
d 4 |
|
|
|
d 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
W |
|
|
|
Jk |
|
|
|
16 |
32 |
|
15 |
|
|
15 |
d |
3 ‒ момент сопротивления бруса кручению |
|||||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
z2 |
|
|
ymax |
|
|
d |
|
|
16 |
|
16 |
256 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на 2-ом участке; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
M z |
2 |
2,648qa2 ‒ крутящий момент на 2-ом участке; |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Лист |
Изм. Лист |
|
|
|
№ докум. |
|
Подпись Дата |
|
|
|
КР-СМ-НГТУ-12КС3-012-14 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
