7
Нормальное распределение (распределение Гаусса)
Аппарат математической статистики достаточно хорошо разработан применительно к условию, когда распределение случайной величины подчиняется закону нормального распределения (закон Гаусса).
Исследованиями в технологии машиностроения установлено, что большинство характеристик технологических процессов подчиняется именно этому закону.
Нормальный закон распределения играет исключительно важную роль во всех областях техники и технологии и занимает особое положение среди других законов распределения.
Нормальное распределение случайной величины возникает в тех случаях, когда результат испытаний является следствием влияния большого количества факторов, среди которых нет доминирующих, а объем наблюдений достаточно велик. Многие непрерывные наблюдения при увеличении объема испытаний стремятся к нормальному распределению.
Случайная величина распределена по нормальному закону, если уравнение плотности распределения вероятности имеет вид:
|
|
|
|
(Y −Y |
)2 |
|
|
|
|
1 |
− |
o |
|
|
|
|
|
2σo2 |
|
|
|
||
|
ϕ(Y ) = |
σo 2π e |
|
|
. |
|
|
Параметрами |
закона |
нормального |
распределения |
являются |
|||
среднеквадратическое отклонение σ0 и среднее значение Yо .
Точную формулу для функции распределения, подчиненного нормальному закону, получить нельзя, так как выражение плотности вероятности представляет неинтегрируемую функцию. Для расчета вероятности попадания случайной величины в какой-либо интервал используется функция Лапласа. Значения функции Лапласа табулированы и представлены в справочниках и учебниках по теории вероятности.
ϕ(Y) 1σo 
2π
M(Y) |
Y |
±σo |
|
±2σo
±3σo
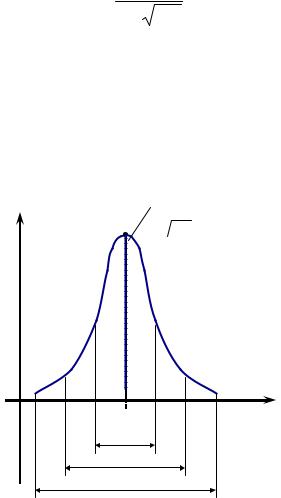
Кривая закона нормального распределения
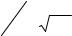
8
Теоретическая кривая закона нормального распределения имеет колоколообразный вид, симметричный относительно перпендикуляра к оси абсцисс, проходящего через точку на оси абсцисс с координатой Yо, достигает максимума в этой точке ( 1σ0 2π ) и асимптотически приближается к нулю
при ± ∞.
Математическое ожидание: M(Y) = Y0 . Дисперсия: D(Y) = σ02 .
Площадь под кривой, ограниченная интервалом Y1≤Y0≤Y2, соответствует вероятности того, что результаты эксперимента попадут в данный интервал. В пределах ±3σ0 от Y0 находится 99,73% площади под кривой.
Поэтому на практике для нормального распределения применяют «правило трех сигм». Для закона нормального распределения на основании «правила трех сигм» поле рассеяния р случайной величины составляет:
p= (Yo +3σo ) −(Yo −3σo ) = 6σo .
Всвязи с тем, что оценивать σ0 и х0 можно с помощью характеристик S и x выборки, практическое поле рассеяния определяют по формуле:
p = 2 l S,
где l – табличное значение коэффициента, взятое при данном объеме выборки для α=0,95 (причем l рассчитано из условия, что количество значений случайных величин, находящихся в пределах практического поля рассеяния, составляет 99,73 %).
Примерами нормального закона распределения могут служить:
–распределение погрешности измерительных приборов;
–характеристики измерения показателя в партии одинаковых изделий;
–погрешности позиционирования станков с ЧПУ, роботов и т.п.