Теорія ймовірностей (Задачі)

3. З цифр «4», «7», «9» складають числа. Скільки можна скласти: а) трицифрових чисел так, щоб жодна з них не повторювалась; б) трицифрових чисел; в) двоцифрових чисел так, щоб жодна з них не повторювалась; г) двоцифрових чисел?

а)

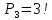
б)

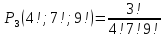
в)

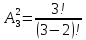
г)

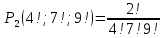
7. Скільки різних дільників має число 2310?

Розкладемо число 2310 на прості множники і складатимемо їх різні добутки (від 1 до 5 множників), тобто скла- датимемо різні підмножини. 2310 = 2 *3⋅5* 7⋅11 — усього п’ять множників. Тоді маємо:

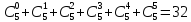
6. Яку кількість різних натуральних чисел можна скласти з цифр 0, 2, 3, 4, щоб в кожне таке число кожна цифра входила не більше одного разу?

одноцифрових =

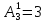
двоцифрових =

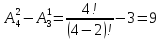
трицифрових =

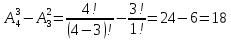
чотирицифрових =

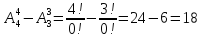
всього = 3+9+18+18 = 48

10. У ящику 20 деталей, серед яких 4 браковані. Скількома способами можна взяти: а) 5 деталей; б) дві браковані; в) одну браковану і чотири стандартні; г) шість деталей, серед яких хоча б одна бракована; д) дві однакові за якістю?

а)

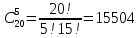
б)

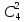
в)

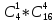
21. Знайти ймовірність того, що дні народження 12 осіб припадуть на різні місяці року.

n = 12¹²

m = 12!

P(A) =

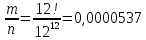
22. Студент прийшов на екзамен підготувавши 20 з 25 питань, екзаменатор задав йому 3 питання. Знайти ймовірність тго, що студент знає відповіді на всі питання.

Аі – випадкова подія

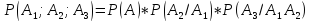
Р(А) =

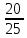
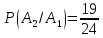
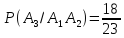
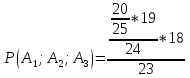= 0,497

27. На книжковій полиці випадковим чином розставляють 4 книги з економіки і три книги з географії. Яка ймовірність того, що книги з одного предмета стоятимуть поруч?

P₄*P₃ =

30. Десять осіб випадковим чином сідають за круглий стіл. Знайти ймовірність того, що чотири певні особи опиняться поруч.

Р(А) = 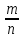Загальна кількість рівноможливих способів розмістити 10 осіб на 10 місцях за круглим столом дорівнює кількості перестановок із 10 елементів, тому n! = 10!

4 певні людини можна розмістити поруч 4! способами. Інших 6 людей можна розмістити 6! способами. За круглим столом (10 місць) пару певних 4 людей можна розмістити 10 спосо- бами.

m = 4!*6!*10

P(A) =

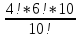
32. А та В і ще 8 осіб стоять у черзі. Знайти ймовірність того, що між А та В стоять три особи.

n = 2+8 = 10 r =3

P(A) =

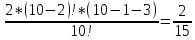
33. З урни, в якій лежать 12 білих і 8 червоних кульок, беруть послідовно дві кульки. Відомо, що перша кулька виявилась білою. Яка ймовірність того, що друга кулька виявиться: а) білою; б) червоною?

А – взята біла кулька

В – взята червона кулька

Якщо першою взяли білу кулю, то в урні залишилося 11 білих кулі та 8 червоних, тому

а)

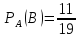
б)

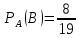
42. Маємо 8 квитків вартістю по 16 гривень, 2 квитки по 35 гривень, 3 квитки по 44 гривень. Навмання беруть три квитки. Знайти ймовірність того, що принаймні два з них мають однакову вартість.

Розв’язання

Нехай А1, А2 та А3 – події за якої серед взятих квитків 2 виявились по 16 гривень, 35 гривень та по 44 гривень відповідно. А4 та А5 - 3 квитки виявились по 16 гривень та по 44 гривень відповідно. А- принаймі два квитка мають однакову вартість.

Р(А)=Р(А₁)+ Р(А₂)+ Р(А₃)+ Р(А₄)+ Р(А₅)

44. З двох гармат зроблено по одному пострілу. Ймовірність влучення з першої гармати – 0,9, з другої – 0,6. Знайти ймовірність: а) одного влучення; б) принаймні одного влучення.

a) p1*q2 + q1*p2 =

б) 1 – q1*q2 = 1 – 0,1*0,4 =

45. (д\з) Два стрільці влучають у ціль з ймовірностями 0,7; 0,8 відповідно. Кожен з них робить один постріл. Яка ймовірність того, що: а) обидва влучать; б) жоден не влучить; в) принаймні один влучить; г) лише один влучить у ціль?

a) p1*p2 =

б) q1*q2 =

в) 1 – q1*q2 =

г) p1*q2 + q1*p2 =

55. Два стрільці незалежно один від одного роблять по одному пострілу по мішені. Ймовірність влучення першого – 0,8, другого – 0,4. Відомо, що є одне влучення. Знайти ймовірність того, що в мішень влучив перший стрілець.

Позначимо випадкові події:   Х1:”влучив перший стрілець”,   Х2:”влучив другий стрілець”,   Y: “є одне влучення у мішень”,   Z: “влучив другий, а перший не влучив”  Апріорна ймовірність того, що при одному пострілі влучить другий стрілець і не влучить перший, (подія Z) визначаємо як ймовірність перерізу (добутку) подій :”перший не влучив” і Х2:”другий влучив”.  За умовою  Ймовірність події Y дорівнює (згідно з теоремами множення і додавання):  В силу незалежності подій Х1 та Х2, і враховуючи, що ймовірність події Z – це умовна ймовірність події Х2 при умові події , знаходимо  З іншого боку, подію Z можна подати як переріз події Y та події Х2 при умові, що подія Y здійснилася. Згідно з теоремою множення  ,  де  – апостеріорна ймовірність того, що наявне одне влучення у мішень зроблено другим стрільцем.  Звідси знаходимо шукану ймовірність того, що влучив другий стрілець при умові, що є одне попадання: 

43. Студент забув останню цифру номера телефону і набирає її навмання. Яка ймовірність того, що йому доведеться набрати номер не більше трьох разів?

Нехай А – описана подія. Її імовірність рівна сумі імовір- ностей несумісних подій В₁ ,В₂ ,В₃ - В₁ – цифра набрана вірно з першого разу.

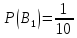
В₂ – цифра набрана вірно з другого разу, отже з першого разу вона не вгадана

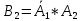
,оскільки

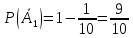
В₃ – цифра набрана вірно з третього разу, тоді

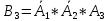
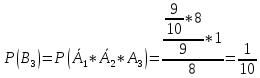,оскільки

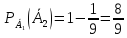
P(A) = P(B1+B2+B3) = P(В1)+Р(В2)+Р(В3) =

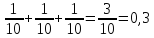
34. В урні 10 білих і 5 чорних кульок. З урни одну за одною беруть дві кульки. Яка ймовірності того, що другою буде взята біла кулька?

Нехай подія В₁ полягає в тому, що першою з урни навмання взяли білу кульку; В₂ — у тому, що першою з урни навмання взяли чорну кульку; подія А — у тому, що друга взята кулька виявилась білою. Для події В₁ з 15 можливих результатів сприятливими є 10, тобто

Р(В₁) =

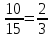
для події В₂ з 15 можливих результатів сприятли- вими є 5, тобто

Р(В₂) =

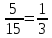
Для події А за умови, що подія В₁ відбулася, з 14 можливих результатів, що залишились, сприятливими є 9 тобто:

Р_в1(А) =

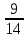
для події А за умови, що подія В₂ відбулася, з 14 можливих результатів, що залишились, сприятливими є 10, тобто

Р_в2(А) =

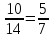
Отже: A = B₁ ⋅ A + B₂ ⋅ A , тоді

Р(А) = Р(В₁А) + Р(В₂А) = Р(В₁)*Р_в1(А) + Р(В₂)*Р_в2(А)=

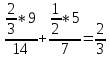
35. В одному ящику 5 білих та 10 червоних кульок, у другому 10 білих та 5 червоних кульок. З кожного ящика навмання беруть по одній кульці. Знайти ймовірність того, що буде вийнято одну білу кульку.

Нехай подія А — навмання взята кулька виявилась білою; подія — навмання взята кулька виявилась червоною.

Події: H₁ — кульку дістали з першої урни, H₂ — із другої

Р(Н₁) = Р(Н₂) =

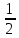
Р(Н₁) + Р(Н₂) = 1

Умовні ймовірності події А: (Р_н1) 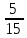— імовірність дістати білу кульку з першої урни;

Умовні ймовірності події А: (Р_н2)

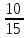
За формулою повної ймовірності:

Р(А) = Р(Н₁)*Р_н1(А) + Р(Н₂)*Р_н2(А) =

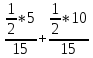
36. В урні чотири білі та три чорні кульки. Два гравці по черзі виймають по одній кульці, не повертаючи їх до урни. Виграє той, який першим витягне білу кульку. Знайти ймовірність подій:

А – виграє перший гравець;

В – виграє другий гравець.

Нехай A - поява білої кулі у першої людини; B - поява білої кулі у другої людини. Якщо подія A відбулася, то P(B) = 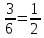. Якщо відбулася подія 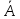- поява чорної кулі у першої людини, то P(B) =

41. Навмання називають одне з чисел від 100 до 999. Яка ймовірність того, що в цьому числі принаймні дві цифри однакові?

Події «взяли навмання число N» (N = 100, 101, ..., 999) різновірогідні (у цьому сенс слова «навмання») і утворюють безліч випадків цього досвіду. Число випадків n = 900. Нас цікавить подія А - «у обраного числа збігаються хоча б дві цифри». Простіше, однак, підрахувати ймовірність протилежного події 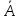 - «у обраного числа всі цифри різні». 

Кожне таке число є розміщення без повторень з 10 цифр по 3, що не має першим елементом нуль. Отже, m =

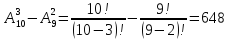
P(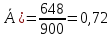 , тоді Р(А) = 1 – Р(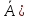 = 1 – 0,72 = 0,28

47. Ймовірність принаймні одного влучення в ціль при трьох пострілах дорівнює 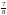. Знайти ймовірність влучення при одному пострілі.

Розв’язання. Ймовірність влучення по мішені хоча б при одному з трьох пострілів (подія А ) дорівнює

де q - ймовірність того, що стрілок промахнеться.

За умовою Р(А)=0,875. Отже, 0,875= 1- q³ =1- 0,875 = 0,125. Звідси .

Шукана ймовірність Р(А) = 1-0,5=0,5.

58. Серед п екзаменаційних білетів т «щасливих». Студенти підходять за білетами один за одним. У кого більша ймовірність взяти «щасливий» білет: у того, хто підійшов першим, чи у того, хто підійшов другим?

А – 1-й витягнув щасливий

В – 2-й витягнув щасливий

гіпотеза:

Н1 – 1-й щасливий

Н2 – 1-й не витягнув щасливий

Р(В) = Р(Н1)*Р(В/Н1)+Р(Н2)*Р(В/Н2)

Р(Н1) =

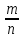
P(H2) =

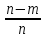
P(B/H1) =

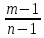
P(B/H2) =

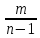
P(B) =

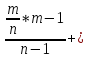
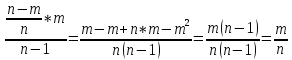
немає значення яким заходити

63. Ймовірність появи деякої події у одному випробуванні 0,8. Яка ймовірність того, що при 8-ми випробуваннях, подія відбудеться: а) 5 разів; б) 0 разів; в) 8 разів; г) не менше 4 разів; д) більше 2 разів; е) не менше 2-х, але менше 5-ти разів; є) принаймні один раз.

а) 5 разів

Р₈ (5) =

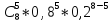
г) не менше 4 разів;

Р₈ (4) =

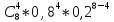
Р₈ (5) =

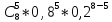
Р₈ (6) =

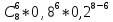
Р₈ (7) =

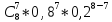
Р₈ (8) =

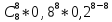
P(4 < x <8) = додаємо всі розраховані ймовірності

д) більше 2 разів;

Р₈ (2) =

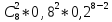
Р₈ (3) =

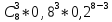
Р₈ (4) =

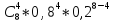
Р₈ (5) =

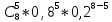
Р₈ (6) =

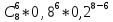
Р₈ (7) =

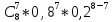
Р₈ (8) =

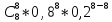
P(2 < x <8) = додаємо всі розраховані ймовірності

е) не менше 2-х, але менше 5-ти разів;

Р₈ (2) =

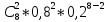
Р₈ (3) =

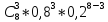
Р₈ (4) =

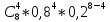
Р₈ (5) =

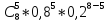
P(2 < x <5) = додаємо всі розраховані ймовірності

є) принаймні один раз.

Р₈ (0) =

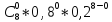
P(1 < x <8) = 1 – P₈ (0)

64. Ймовірність появи деякої події у одному випробуванні 0,7. Яка ймовірність того, що при 120-ти випробуваннях, подія відбудеться: а) 10 разів; б) 0 разів; в) 84 рази; г) не менше 100 разів; д) не більше 20 разів; е) від 80 до 100 разів.

а) 10 разів

Локальна теорема Муавра-Лапласа:

Рn(R) =

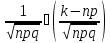
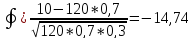
Р₁₂₀(10) =

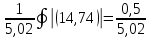
г) не менше 100 разів

Інтегральна теорема Муавра-Лапласа

Pn = (k1 ≤ k ≤ k2) ≈ ∮ -

∮

∮

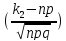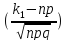
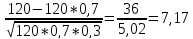
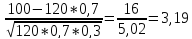
P₁₂₀ = (100 ≤ k ≤ 120) ≈ ∮(7,17) - ∮(3,19) = 0,5 - 0,0025 =

65. Ймовірність появи деякої події у одному випробуванні 0,004. Яка ймовірність того, що при 1000 випробуваннях, подія відбудеться: а) 5 разів; б) 0 разів; в) 10 разів; г)менше 5 разів; д) не більше 3 разів; е) від 3 до 5 разів.

Рn(K) ≈ p(K) = 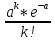, a = np(*)

Ця формула дає досить точне наближення при невеликих р (менше ніж 0,1) і добуток npq ≤ 9

Для знаходження ймов. a = np(*) використовуємо таблицю.

а) 5 разів

a = np = 1000*0,004 = 4

P₁₀₀₀(5) =

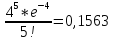
г)менше 5 разів

P₁₀₀₀(k < 5) =

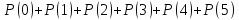
70. Ймовірність появи події А в кожному з 10 незалежних випробувань дорівнює 0,2. Знайти найімовірнішу частоту появи події А у 10 незалежних повторних випробуваннях.

np − q ≤ m₀ ≤ np + p

Частота m₀ є цілим числом. Останню нерівність задовольняє лише одне ціле значення

71. Ймовірність появи події А в кожному з п незалежних випробувань дорівнює 0,8. Скільки таких випробувань потрібно виконати, щоб найімовірніша частота появи події А в цих випробуваннях дорівнювала 30?

np − q ≤ m₀ ≤ np + p

0,8*n – 0,2 ≤ 30 ≤ 0,8*n + 0,8

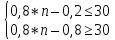
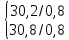
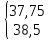
Необхідно провести 38 або 39 незалежних випробувань

81. Імовірність появи “успіху” в кожному з 100 незалежних випробувань дорівнює 0,7. Знайти таке додатне число , щоб з ймовірністю 0,7777 абсолютна величина відхилення відносної частоти появи успіху від його ймовірності 0,7 не перевищила .

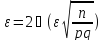
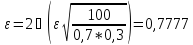
ϕ (21,82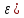 = 0,3888

За таблицею знаходимо ст. 295: 21,82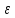 = 1,22

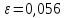
82. Скільки потрібно провести випробувань, щоб з імовірністю 0,96 а гарантувати, що відхилення відносної частоти появи події А від сталої ймовірності її настання не перевищить 0,025? Відомо, що ймовірність настання події А у кожному випробуванні дорівнює 0,7.

Ймовірність події |W(A)-p| ≤  можна розрахувати за формулою:

P{|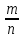 – p| ≤ } ≈ 2 ∮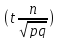

За умовою: р = 0,7 q = 0,3

x = 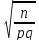 => n =

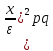
P{|W(A) – 0,7| ≤ 0,025} ≈ 0,96

P{|W(A) – 0,7| ≤ 0,025} ≈ 2 ∮ (0,025

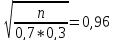
∮(X) = 0,48

X = 2,054

n =

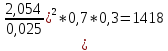
Отже, нелбхідно провести 1418 випробувань.

83. Ймовірність появи події А в кожному з 3 незалежних випробувань різна й дорівнює: р₁=0,5; р₂=0,6; р₃=0,7. Знайти ймовірність того, що внаслідок випробувань подія А з’явиться: а) один раз; б) два; в) три; г) жодного разу.

Імовірності появи події А у випробуваннях різні, тому застосуємо твірну функцію, яка в цьому разі матиме вигляд:

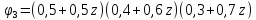
Розкриємо дужки і зведемо подібні доданки:

ділі вирішуємо та знаходимо z – один раз z² – 2 рази і так далі.

Задача №1

Задано ряд розподілу випадкової величини Х:

хі	-3	-2	-1	0	1
рі	0,1	0,05	0,2	0,22	0,05

Побудувати та обчислити: а) многокутник розподілу; б) функцію розподілу; в) графік функції розподілу; г) моду; д) математичне сподівання; е) дисперсію; є) середнє квадратичне відхи-лення; ж) асиметрію; з) ексцес; и) P (–2,5 ≤ Х < 3,5).

а) Будуємо многокутник розподілу

б) Запишемо функцію розподілу F(x)

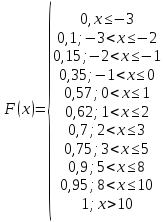
в) Будуємо графік функції розподілу

г) Мода:

М₀ = 0

д) Математичне сподівання:

М(Х) = 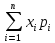= (-3)*0,1 + (-2)*0,05 + (-1)*0,2 + 0*0,22 + 1*0,05 + 2*0,08 + 3*0,05 + 5*0,15 + +8*0,05 + 10*0,05 = 1,41

e) Дисперсія

D(X) = M(X²) – M²(X) = 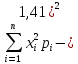= 9*0,1 + 4*0,05 + 1*0,2 + 0*0,22 + 1*0,05 + 4*0,08+ + 9*0,05 + 25*0,15 + 64*0,05 + 100*0,05 – (1,41²) = 12,08

є) Середнє квадратичне відхилення

σ =

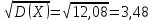
ж) Асиметрія

A_s =

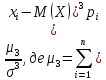
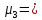(-3-4,41)³*0,1 + (-2-1,41)³*0,05 + (-1-1,41)³*0,2 + (0-1,41)³*0,22 + (1-1,41)³*0,05 + (2-1,41)³*0,08 + (3-1,41)³*0,05 + (5-1,41)³*0,15 + (8-1,41)³*0,05 + (10-1,41)³*0,05 = 39,18

A_s =

з) Ексцес

E_s =

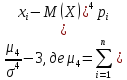
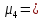(-3-4,41)⁴*0,1 + (-2-1,41)⁴*0,05 + (-1-1,41)⁴*0,2 + (0-1,41)⁴*0,22 + (1-1,41)⁴*0,05 + (2-1,41)⁴*0,08 + (3-1,41)⁴*0,05 + (5-1,41)⁴*0,15 + (8-1,41)⁴*0,05 + (10-1,41)⁴*0,05 = 443,98

E_s =

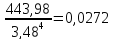
и) Р (-2,5 ≤ X < 3,5) = P(x = -2) + P(x = -1) + P(x = 0) + P(x = 1) + P(x = 2) + P(x = 3) = 0,05 + 0,2 + 0,22 + 0,05 + 0,08 + 0,05 = 0,65

92. Відмова у виконанні певної операції для кожної фінансової установи дорівнює 0,9. Знайти середню кількість відмов та дисперсію відмов у десяти фінансових установах.

M(X) = np = 10*0,9 =

D(X) = npq = 10*0,9*0,1

94. Величина Х розподілена за законом Пуассона з 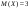. Побудувати многокутник розподілу, функцію розподілу 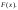Знайти : а) 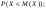б)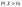

98. Стрілець стріляє в мішень допоки влучить. Ймовірність влучення при одному пострілі дорівнює 0,7. Знайти середню кількість вдалих пострілів та дисперсію кількості пострілів.

геометричний розподіл

М(Х) =

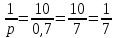
D(X) =

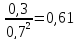
99. В партії із 50 виробів знаходиться 5 бракованих виробів. Здійснюється безповторна вибірка 6 виробів. Побудувати закон розподілу величини Х – кількості бракованих виробів серед відібраних. Знайти M(X) та D(X)

гіпергеометричний закон розподілу

N = 50 n = 5 k = 6

p = P(X=m) =

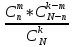
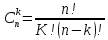
p = P(X=1) =

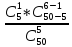
p = P(X=2) =

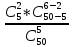
і так далі до 6, а далі закон розподілу

M(X) =

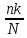
D(X) =

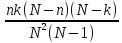
97. Знайти дисперсію успіху при 20 випробуваннях , якщо ймовірність успіху в кожному випробуванні дорівнює 0,2.

біноміальний розподіл

D(X) = npq = 20*0,2*0,8 = 3,2

96. Знайти математичне сподівання числа лотерейних білетів, на які випадуть виграші, якщо придбано 20 білетів і ймовірність виграшу по одному білету дорівнює 0,05.

розподіл Пуасона

а = np = 20*0,05 = 1

M(X) = D(X) = a = 1

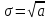
95. Ймовірність того, що грошовий приймач автомата при подачі грошей спрацює правильно, дорівнює 0,97. Скласти закон розподілу величини Х – числа подачі грошей в автомат :

а) до першої правильної роботи автомата;

б) до першої неправильної роботи автомата.

геометричний закон розподілу

Можливі значення величини X = {1, 2, 3, ...}. Подія А — перша правильна робота автомата

X	1	2	3	….	m
p	0,97	0,03*0,97	0,032*0,97	….	0,03m-1*0,97

Подія 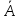— перша неправильна робота автомата

X	1	2	3	….	m
p	0,97	0,97*0,03	0,972*0,03	….	0,97m-1*0,03

100. В біноміальному випробуванні п =15 , р = 0,05. Знайти 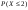та 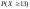. Пояснити результат.

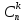P_n (K) = * p^k * q^n-k

P(X ≥ 13) = P (X=13) + P(X = 14) + P(X = 15)

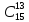P₁₅ (13) = * 0,05¹³ * 0,95^15-13

і так далі

104. Випадкова величина X розподілена за нормальним законом. Математичне сподівання і середнє квадратичне відхилення цієї величини відповідно дорівнюють 25 і 15. Знайти ймовірність того, що X набуде таких значень: а) X належать інтервалу (10; 40); б) X більше 40; в) X менше 10.

P (

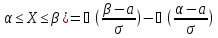
P (

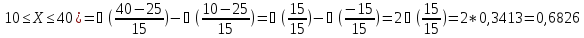
106. Електронна лампа працює справно протягом випадкового часу T, розподіленого за показниковим законом:

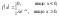
Після того, як лампа вийде з ладу, її замінюють іншою. Знайти ймовірність того, що за час t : а) лампу не доведеться замінювати; б) лампу доведеться замінити рівно три рази; в) лампу доведеться замінити не менше трьох раз.

a) P₀ =

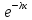
б) Р₃ =

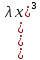
в) R₃ = 1 – (P₀ + P₁ + P₂) = 1 -

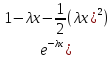
107. Під час роботи деякого приладу у випадкові моменти часу виникають несправності. Час T роботи приладу від його

ввімкнення до його відключення розподілено за показниковим законом:

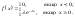
При виникненні несправності вона миттєво виявляється, і прилад ремонтується. Ремонт продовжується час t, після чого прилад знову починає використовуватись. Знайти щільність розподілу, функцію розподілу проміжку часу T між двома сусідніми несправностями. Обчислити .
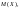
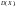
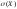