
6 (1)
.docВаріант №7 А=6 В=5
№1.
Серед студентів університету навмання обирають одного. Подія А полягає в тому, що обраним студентом є хлопець, подія В полягає в тому, що студент навчається на вечірньому відділені, подія С -у тому, що студент працює у банку. Записати у чому полягають події:
1.
![]() 2.
2.
![]()
Розв’язання
1)
![]() - обраний студент не є хлопцем, який
навчається на вечірньому відділені і
не працює в банку.
- обраний студент не є хлопцем, який
навчається на вечірньому відділені і
не працює в банку.
2)
![]() - обраний студент є хлопцем, який працює
в банку
- обраний студент є хлопцем, який працює
в банку
або - обраний студент не є хлопцем, який не працює в банку.
№2.
Після співбесіди з 16 особами, правління інвестиційної компанії обирає для працевлаштування 5 осіб.
1. Скільки різних можливостей послідовності проходження співбесіди має кожна особа?
2. Скільки різних можливостей обрання 5 осіб має інвестиційна компанія, якщо
А) всі обрані особи приймаються на одну посаду?
Б) всі обрані особи приймаються на різні посади?
Розв’язання
1) Переставленням із n елементів називають такі впорядковані множини з n елементів, які різняться між собою порядком їх розміщення.
Кількість таких упорядкованих множин обчислюється за формулою
![]() ,
,
де n набуває лише цілих невід’ємних значень. Тому підставивши значення умови задачі отримаємо:
n=16!=1•2•3•4•5•6•……..•11•12•13•14•15•16=20922789888000
2)
А) Комбінаціями
з n
елементів по
![]() називаються такі множини з m
елементів, які різняться між собою хоча
б одним елементом.
називаються такі множини з m
елементів, які різняться між собою хоча
б одним елементом.
Кількість
таких множин
![]() .
.
![]()
Б) Коли всі обрані особи приймаються на різні посади , то кількість можливостей буде рівна
![]()
№3.
Троє студентів домовились про зустріч. Ймовірність того, що кожен з трьох студентів з'явиться дорівнює 0,76; 0,55 ; 0,7. Знайти ймовірність того, що зустріч відбудеться, якщо для цього достатньо, щоб на зустріч прийшли принаймні два студента.
Розв’язання
Ймовірність, того що всі три студенти прийдуть за зустріч знайдемо за формулою: Р=р1·р2·р3
![]()
Ймовірність,
того що двоє студенти прийдуть за
зустріч :![]()
![]()
Тоді ймовірність зустрічі складатиме: Р=0,2926+0,4572=0,7498
№4.
В студентській групі 26 осіб, серед них 20 студентів віком старше 19 років, та а студентів віком старше
20 років. Розігрується один білет на виставу. Чому дорівнює ймовірність того, що цей білет отримає студент віком старше 19 років або студент віком старше 20 років?
Розв’язання
Нехай А - білет отримає студент віком старше 19 років або студент віком старше 20 років.
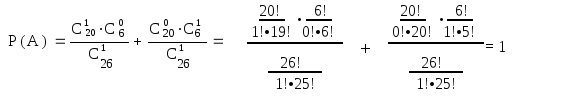
№5.
Ймовірність знайти необхідний товар у однієї крамниці дорівнює 0,5, а ймовірність домовитись про його купівлю - 0,6. Обчислити ймовірність придбання товару, якщо побувати не більше ніж у 5 крамницях.
Розв’язання
Імовірність появи випадкової події принаймні один раз при n незалежних спробах
![]() Якщо
Р(Аі)
= pі
= p
= const, то qі
= q
= const. Тоді Р(С)
= 1 – qn.
Якщо
Р(Аі)
= pі
= p
= const, то qі
= q
= const. Тоді Р(С)
= 1 – qn.
Обчислимо ймовірність покупки для одного магазину: Р=р1·р2
Р=0,5•0,6=0,3. Тоді ймовірність не купівля буде рівна: q=1-p=1-0,3=0,7
Отже ймовірність придбання товару, якщо побувати не більше ніж у 5 крамницях складатиме:
![]()
№6
На промисловому підприємстві встановлено систему пожежної сигналізації. Якщо виникає пожежа, сигналізація спрацьовує з ймовірністю 0,95. Але сигналізація може спрацювати випадково
(коли пожежі немає) з ймовірністю 0,12. Ймовірність настання пожежі 0,02. Сигналізація спрацювала. Чому дорівнює ймовірність того, що почалась пожежа?
Розв’язання
Формулу
Байєса використовують для переоцінювання
ймовірностей гіпотез Ві
за умови, що випадкова подія А здійсниться
, тобто
![]()
Нехай В1 та В2 – пожежа настала та відсутня відповідно. А – сигналізація спрацювала, тоді
![]()
№7
Ймовірність того, що впродовж робочого дня не виникне порушення у забезпеченні сировиною, дорівнює 0,86. Знайти ймовірність того, що впродовж робочого тижня (5 днів):
а) в продовж трьох робочих днів не буде порушень у забезпеченні сировиною;
б) порушення будуть менше, ніж в продовж трьох днів ;
в) порушення виникнуть не менше, як впродовж одного дня , але не більше ніж впродовж трьох днів.
Розв’язання
а) Імовірність того, що в результаті n незалежних експериментів за схемою Бернуллі подія А з’явиться m раз, подається у вигляді
![]()
![]()
б) порушення будуть менше, ніж в продовж трьох днів ;
![]()
![]()
Р(3<X<5)=0,1247+0,3829+0,4704=0,978
в) порушення виникнуть не менше, як впродовж одного дня , але не більше ніж впродовж трьох днів.
![]()
Р(2<X<4)=0,0203+0,1247+0,3829=0,5279
№8.
Ймовірність влучення в мішень при одному пострілі дорівнює 0,96. Зайти ймовірність того, що при 100 пострілах мішень буде уражена :
а) 42 разів; б) не менше 45 разів та не більше 50 разів?
Розв’язання
а) Якщо
ймовірність появи випадкової події в
кожному з n
незалежних експериментів є величиною
сталою і дорівнює
![]() ,
то для великих значень n
і m
імовірність того, що випадкова подія А
настане m
раз, подається такою асимптотичною
формулою:
,
то для великих значень n
і m
імовірність того, що випадкова подія А
настане m
раз, подається такою асимптотичною
формулою:
![]() ,
де
,
де
![]() .
.
![]()
![]()
б) Якщо
ймовірність появи випадкової події в
кожному з n
незалежних експериментів є величиною
сталою і дорівнює
![]() ,
то для великих значень n
імовірність появи випадкової події від
mі
до mj
раз обчислюється за такою асимптотичною
формулою:
,
то для великих значень n
імовірність появи випадкової події від
mі
до mj
раз обчислюється за такою асимптотичною
формулою:
![]() ,
де
,
де
![]()
![]() ,
,
![]()
![]() №9.
№9.
4006 автомобілів було відправлено на продаж. Ймовірність того, що автомобіль буде з дефектом дорівнює 0,01 . Яка ймовірність того, що 5 автомобілів із цієї загальної кількості будуть з дефектами?
Розв’язання
За умови
np = a = const
імовірність появи випадкової події m
раз
![]() обчислюється за такою асимптотичною
формулою:
обчислюється за такою асимптотичною
формулою:
![]() де а=n·p
де а=n·p
а=4006•0,01=40,06
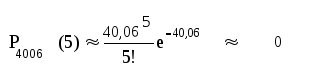
№10.
Скільки потрібно провести випробувань, щоб з ймовірністю 0,96 гарантувати, що відхилення відносної частоти появи події А від сталої ймовірності її настання не перевищить 0,025.
Відомо, що ймовірність настання події А у кожному випробуванні дорівнює 0,7.
Розв’язання
Ймовірність події W(A) – р< ( > 0 і є малою величиною) можна розрахувати за формулою:
![]() За
умовою задачі р=0,7, q=1-p=1-0,7=0,3
За
умовою задачі р=0,7, q=1-p=1-0,7=0,3
![]()
![]()
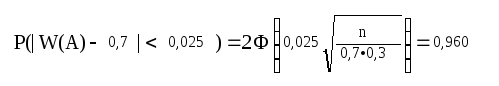
Ф(Х)=0,48. Звідси Х=2,054
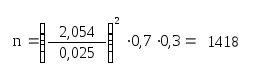
Отже потрібно провести 1418 випробувань.
