6

Варіант №8 А=6 В=5

№1

Три стрільці стріляють по мішені. Подія А - в мішені два влучення. Подія В- в мішені не менше двох влучень. Запишіть простір елементарних подій та події:

Розв’язання

- в мішені одне влучення або жодного

- події не сумісні

- в мішені одне влучення або жодного

№2.

Підприємство для маркування своєї продукції використовує товарний знак, який містить 13 смуг червоного, блакитного та жовтого кольорів. Скільки різних товарних знаків може бути складено для підприємства , якщо відомо, що кожне маркування містить 3 червоні та дві жовті смуги.

Розв’язання

Використаємо розміщення

№3.

В автомобільних гонках прийняли участь 11 автомобілів, які успішно пройшли дистанцію Автомобілі під номером 3 і номером 4 належать одному спортивному клубу. Яка ймовірність того, що ці два автомобілі фінішували один за одним?

Примітка. Жодна пара автомобілів не фінішувала одночасно.

Розв’язання

Нехай А та В – події за якої автомобілі під номер 3 та 4 фінішували відповідно. С- два автомобілі фінішували один за одним

Р(А)=1/11 = 0,0909

Р(В/А)=1/10 = 0,1

Р(С)=Р(А)•Р(В/А)=0,0909•0,1=0,0091

№4

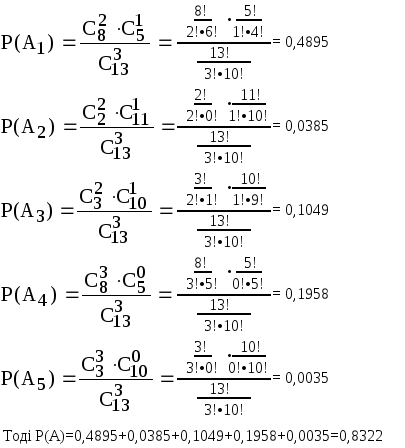
Маємо 8 квитків вартістю по 16 гривень, 2 квитки по 35 гривень, 3 квитки по 44 гривень. Навмання беруть три квитки. Знайти ймовірність того, що принаймні два з них мають однакову вартість.

Розв’язання

Нехай А1, А2 та А3 – події за якої серед взятих квитків 2 виявились по 16 гривень, 35 гривень та по 44 гривень відповідно. А4 та А5 - 3 квитки виявились по 16 гривень та по 44 гривень відповідно. А- принаймі два квитка мають однакову вартість.

Р(А)=Р(А₁)+ Р(А₂)+ Р(А₃)+ Р(А₄)+ Р(А₅)

№5

В аеропорту Бориспіль очікують прибуття трьох міжнародних рейсів. Ймовірність своєчасного

прибуття літака до аеропорту дорівнює : для першого рейсу - 0,76. для другого рейсу -0,65, для третього рейсу -0,8. Знайти ймовірність того, що:

A) принаймні один з літаків прибуде вчасно; Б) не менше двох прибуде вчасно;

B) перший, та третій прибудуть вчасно.

Розв’язання

А)

Б) Ймовірність того, що всі вчасно прибудуть в аеропорт складає:

Ймовірність того, що 2 вчасно прибудуть в аеропорт складає

Тоді ймовірність того, що прибуде не менше двох вчасно рівна

Р=0,3952+0,4364=0,8316

В) перший, та третій прибудуть вчасно

№6

Три робітники виготовляють однотипні деталі, при цьому їх продуктивності співвідносяться як 5:4:6. Ймовірність допустити брак при виготовленні однієї деталі для кожного із робітників

відповідно дорівнює 0,12; 0,15; 0,01. Всі деталі, виготовлені робітниками, складаються до одного контейнеру. Яка ймовірність того, що:

А) навмання взята одна деталь з контейнеру виявиться бракованою: Б) браковану деталь виготовлено другим робітником

Розв’язання

А) Нехай А – деталь виявилась бракованою, В1,В2,В3 – деталь виготовив 1-й, 2-й та 3-й робітник відповідно , тоді запишемо ймовірності подій:

Р(В1)=5/15=0,3333

Р(В2)=4/15=0,2667

Р(В3)=6/15=0,4

Тоді за формулою повної ймовірності знайдемо ймовірність події А:

Р(А)=0,3333•0,12+0,2667•0,15+0,4•0,01=0,084

Б) Використаємо формулу Байєса для знаходження того, що браковану деталь виготовлено другим робітником

№7.

Спортсмен 5 разів стріляє по мішені. Ймовірність влучення в мішень при одному пострілі 0,76. Для одержання заліку необхідно влучити не менше 3-х разів. Знайти

А) ймовірність одержання заліку спортсменом; Б) найбільш ймовірну кількість влучень у мішень.

Розв’язання

А) Імовірність того, що в результаті n незалежних експериментів за схемою Бернуллі подія А з’явиться m раз, подається у вигляді

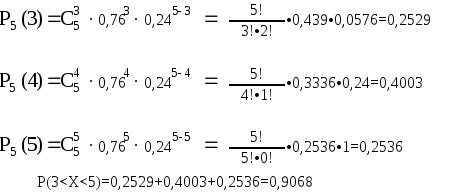
Б) Використовуючи подвійну нерівність знайдемо найвірогідніше число влучень:

5•0,76-0,24 <m<5•0,76+0,76

3,56<m<4,56

Найвірогідніше кількість влучень складає 4.

№8.

Ймовірність присутності студента на занятті дорівнює 0,86. Знайти ймовірність того, що із 60 студентів на занятті будуть присутні: A) рівно 56 студента; Б) не менше ніж 55, але не більше 58 студентів? B) всі.

Розв’язання

а) Якщо ймовірність появи випадкової події в кожному з n незалеж­них експериментів є величиною сталою і дорівнює , то для великих значень n і m імовірність того, що випадкова подія А настане m раз, подається такою асимптотичною формулою:

, де .

б) Якщо ймовірність появи випадкової події в кожному з n незалеж­них експериментів є величиною сталою і дорівнює , то для великих значень n імовірність появи випадкової події від m_і до m_j раз обчислюється за такою асимптотичною формулою:

, де ,

в )

№9

За оцінкою експертів банку, середня кількість платіжних карток, які будуть заблоковані під час користування за різними причинами, дорівнює 0,02%. Знайти ймовірність того, що із 5000 платіжних карток:

А) буде заблоковано 3 картки; Б) не буде заблоковано 4997 картки;

Розв’язання

А) За умови np = a = const імовірність появи випадкової події m раз обчислюється за такою асимптотичною формулою: де а=n·p

а=5000•0,0002=1

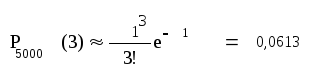
Б)

№10.

На кожні 100 виготовлених деталей припадає у середньому І0 деталей першого сорту. Для

перевірки обирається партія з 600 деталей. У яких межах може міститися відносна частота появи

деталі першого сорту, якщо відхилення її від теоретичної ймовірності потрібно гарантувати з

ймовірністю 0,936. Визначити можливу кількість деталей першого сорту цієї партії за даних умов.

Розв’язання

Ймовірність події W(A) – р<  ( > 0 і є малою величиною) можна розрахувати за формулою:

За умовою задачі р=0,7, q=1-p=1-0,7=0,3

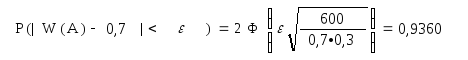
Ф(Х)=0,468. Звідси Х=1,852

Отже відносна частота має бути в межах від 0,6654 до 0,7346

Можлива кількість деталей першого сорту складає: n=600•0,7346=441