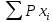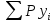1

Варіант – 7 с - 6

Задача №1

Задано ряд розподілу випадкової величини Х:

хі	-3	-2	-1	0	1	2	3	5	8	10
рі	0,1	0,05	0,2	0,22	0,05	0,08	0,05	0,15	0,05	0,05

Побудувати та обчислити: а) многокутник розподілу; б) функцію розподілу; в) графік функції розподілу; г) моду; д) математичне сподівання; е) дисперсію; є) середнє квадратичне відхи-лення; ж) асиметрію; з) ексцес; и) P (–2,5 ≤ Х < 3,5).

а) Будуємо многокутник розподілу

б) Запишемо функцію розподілу F(x)

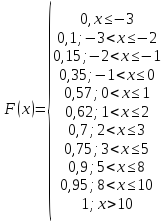
в) Будуємо графік функції розподілу

г) Мода:

М₀ = 0

д) Математичне сподівання:

М(Х) = 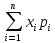= (-3)*0,1 + (-2)*0,05 + (-1)*0,2 + 0*0,22 + 1*0,05 + 2*0,08 + 3*0,05 + 5*0,15 + +8*0,05 + 10*0,05 = 1,41

e) Дисперсія

D(X) = M(X²) – M²(X) = 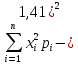= 9*0,1 + 4*0,05 + 1*0,2 + 0*0,22 + 1*0,05 + 4*0,08+ + 9*0,05 + 25*0,15 + 64*0,05 + 100*0,05 – (1,41²) = 12,08

є) Середнє квадратичне відхилення

σ =

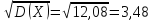
ж) Асиметрія

A_s =

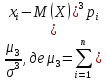
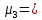(-3-4,41)³*0,1 + (-2-1,41)³*0,05 + (-1-1,41)³*0,2 + (0-1,41)³*0,22 + (1-1,41)³*0,05 + (2-1,41)³*0,08 + (3-1,41)³*0,05 + (5-1,41)³*0,15 + (8-1,41)³*0,05 + (10-1,41)³*0,05 = 39,18

A_s =

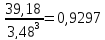
з) Ексцес

E_s =

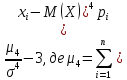
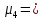(-3-4,41)⁴*0,1 + (-2-1,41)⁴*0,05 + (-1-1,41)⁴*0,2 + (0-1,41)⁴*0,22 + (1-1,41)⁴*0,05 + (2-1,41)⁴*0,08 + (3-1,41)⁴*0,05 + (5-1,41)⁴*0,15 + (8-1,41)⁴*0,05 + (10-1,41)⁴*0,05 = 443,98

E_s =

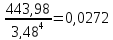
и) Р (-2,5 ≤ X < 3,5) = P(x = -2) + P(x = -1) + P(x = 0) + P(x = 1) + P(x = 2) + P(x = 3) = 0,05 + 0,2 + 0,22 + 0,05 + 0,08 + 0,05 = 0,65

Задача №2

Імовірність пройти перевірку фірми без штрафних санкцій дорівнює 0,06. Відбулося 9 перевірок. Побудувати ряд розподілу випадкової величини Х — кількості перевірок без штрафних санкцій.

p = 0,06 q = 0,94 n = 9

xi	0	1	2	3	4	5	6	7	8	9
pi	0,5730	0,3292	0,0840	0,0125	0,0012	0,0000765	0,0000033	89*10-9	142*10-11	1*10-11

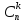P_n (K) = * p^k * q^n-k

P₉ (0) = 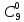* 0,06⁰ * 0,94⁹ = 0,5730

P₉ (1) = 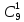* 0,06¹ * 0,94^9-1 = 0,3292

P₉ (2) = 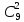* 0,06² * 0,94^9-2 = 0,0840

P₉ (3) = 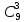* 0,06³ * 0,94^9-3 = 0,0125

P₉ (4) = 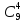* 0,06⁴ * 0,94^9-4 = 0,0012

P₉ (5) = 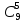* 0,06⁵ * 0,94^9-5 = 0,0000765

P₉ (6) = 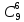* 0,06⁶ * 0,94^9-6 = 0,0000033

P₉ (7) = 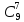* 0,06⁷ * 0,94^9-7 = 0,000000089047 = 89*10^-9

P₉ (8) = 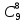* 0,06⁸ * 0,94^9-8 = 0,000000001421 = 142*10^-11

P₉ (9) = 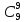* 0,06⁹ * 0,94⁰ = 0,000000000010 = 1*10^-11

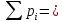0,5730 + 0,3292 + 0,0840 + 0,0125 + 0,0012 + 0,0000765 + 0,0000033 + 0,000000089047 + 0,000000001421 + 0,000000000010 = 1

Задача №4

Час Т безвідмовної роботи двигуна автомобіля розподілений за показниковим законом. Відомо, що середній час напрацювання двигуна на відмову між технічними обслуговуваннями дорівнює 100 год. Визначити ймовірність безвідмовної роботи двигуна за 80 год.

За умовою: М(Х) = 100, Х – час безвідмовної роботи.

Тоді імовірність безвідмовної роботи за 80 годин рівна згідно показникового закону:

Р (

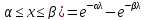
Оскільки М(Х) =

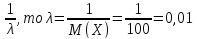
Отже, Р (0 ≤ х ≤ 80) =

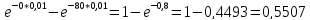
Задача №5

Випадкова величина Х є нормально розподіленою з математичним сподіванням m = 21 і дисперсією D = 3. Записати вирази для щільності розподілу ймовірностей f(x) та функції розподілу F(x) і побудувати їхні графіки. Обчислити ймовірність попадання випадкової величини на проміжок (14, 22]. Яка ймовірність відхилення випадкової величини від її математичного сподівання більше ніж на 1,2 одиниці?

За умовою: m = 21, D = 3, то σ =

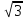
Щільність нормально розподіленої випадкової величини визначається за формулою

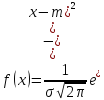
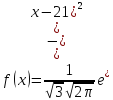
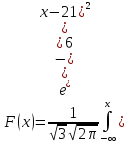
Імовірність попадання випадкової величини Х на (14; 22]

P (14 < X ≤ 22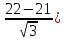) = ϕ ( – ϕ (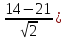 = ϕ (0,58) – ϕ (-4) = 0,2190 + 0,5 = 0,719 = 71,9%

Імовірність відхилення випадкової величини Х від її математичного сподівання більше ніж на 1,2 одиниці: P (| X – 21 | > 1,2) = 1 - P (| X – 21 | ≤ 1,2) = 1 - 2ϕ (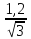) ≈ 1 - 2ϕ(0,69) = 1 – 2*0,2549 = 0,4902

Графіки F(x) та f (x):

Задача №6

До крамниці зайшли три покупці. Ймовірності того, що кожний з них здійснить купівлю, відповідно дорівнюють 0,9; 0,8 та 0,7. Скласти закон розподілу кількості покупців, які здійснили купівлю, та обчислити математичне сподівання і дисперсію цієї випадкової величини.

Випадкова величина Х – покупець здійснить купівлю товару.

Р {X = 0} = 0,1*0,2*0,3 = 0,006

P {X = 1} = 0,9*0,2*0,3 + 0,1*0,8*0,3 + 0,1*0,2*0,7 = 0,092

P {X = 2} = 0,9*0,8*0,3 + 0,1*0,8*0,7 + 0,9*0,2*0,7 = 0,398

P {X = 3} = 0,9*0,8*0,7 = 0,504

xi	0	1	2	3
pi	0,006	0,092	0,398	0,504

Математичне сподівання:

М(Х) = 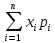= 0*0,006 + 1*0,092 + 2*0,398 + 3*0,504 = 2,4

Дисперсія

D(X) = M(X²) – M²(X) = 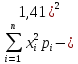= 0*0,006 + 1*0,092 + 4*0,398 + 9*0,504 – (2,4²) = 0,46

Задача №7

Система випадкових величин (Х, Y) задана таблицею розподілу:

X Y	-5	-4	-3	-2	-1	6
-2	0,01	0,02	0,02	0,01	0,02	0,06	0,14
-1	0,03	0,05	0,04	0,01	0,02	0,01	0,16
0	0,06	0,05	0,01	0,04	0,07	0,09	0,32
1	0,04	0,03	0,03	0,03	0,08	0,02	0,23
4	0,05	0,01	0,04	0,03	0,01	0,01	0,15
	0,19	0,16	0,14	0,12	0,2	0,19	1

Знайти: а) двовимірну функцію розподілу; б) ряди розподілу кожної випадкової величини; в) одновимірні функції розподілу; г) числові характеристики системи: математичне сподівання, дисперсію, кореляційний момент; д) умовне математичне сподівання випадкової величини Y, якщо випадкова величина Х набула значення 6.

а) Побудуємо двовимірну функцію розподілу F (x; y) = )

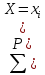б) Ряди розподілу випадкових величин

Ряд розподілу випадкової величини Х:

X	-5	-4	-3	-2	-1	6
Pxi	0,19	0,16	0,14	0,12	0,2	0,19

Ряд розподілу випадкової величини Y :

Y	-2	-1	0	1	4
Pyi	0,14	0,16	0,32	0,23	0,15

в) Будуємо одновимірні функції розподілу:

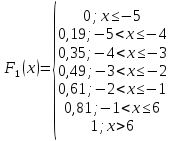
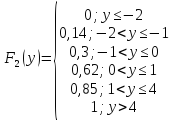
г) Числові характеристики системи: математичне сподівання, дисперсію, кореляційний момент;

М(Х) = (-5)*0,19 + (-4)*0,16 + (-3)*0,14 + (-2)*0,12 + (-1)*0,2 + 6*0,19 = -1,31

М(Y) = (-2)*0,14 + (-1)*0,16 + 0*0,32 + 1*0,23 + 4*0,15 = 0,39

D(X) = 25*0,19 + 16*0,16 + 9*0,14 + 4*0,12 + 1*0,2 + 36*0,19 – 1,72 = 14,37

D(Y) = 4*0,14 + 1*0,16 + 0*0,32 + 1*0,23 + 16*0,15 – 0,15 = 3,2

K_xy = M(XY) – M(X)*M(Y)

M(XY) = -5 *((-2)*0,01 + (-1)*0,03 + 0*0,06 + 1*0,04 + 4*0,05) +

+ (-4)* ((-2)*0,02 + (-1)*0,05 + 0*0,05 + 1*0,03 + 4*0,01) +

+ (-3)* ((-2)*0,02 + (-1)*0,04 + 0*0,01 + 1*0,03 + 4*0,04) +

+ (-2)* ((-2)*0,01 + (-1)*0,01 + 0*0,04 + 1*0,03 + 4*0,03) +

+ (-1)* ((-2)*0,02 + (-1)*0,02 + 0*0,07 + 1*0,08 + 4*0,01) +

+ 6*((-2)*0,06 + (-1)*0,01 + 0*0,09 + 1*0,02 + 4*0,01) = -1,92

K_xy = -1,92 - (-1,31)*0,39 = -1,41

д) Умовне математичне сподівання випадкової величини Y, якщо випадкова величина Х набула значення 6.

Y	-2	-1	0	1	4
Px = 6	0,3158	0,0526	0,4737	0,1053	0,0526

P {Y = -2 / X = 6} = =

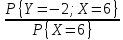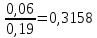
P {Y = -1 / X = 6} = =

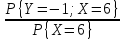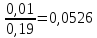
P {Y = 0 / X = 6} = =

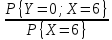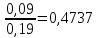
P {Y = 1 / X = 6} = =

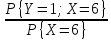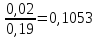
P {Y = 4 / X = 6} = =

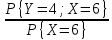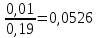
M(Y/X = 6) = (-2)*0,3158 + (-1)*0,0526 + 1*0,1053 + 4*0,0526 = -0,3685