Теорія ймовірностей (Задачі)

T* = T + t₀

f(x) =

F(x) =

M(X) = =

D (X) =

P(T >2t₀) = 1 –F(2t₀) =

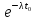
110. Задано математичне сподівання а =10 та середнє квадратичне відхилення нормально розподіленої випадкової величини Х. Знайти :

1.

2.

P (6< X<16) = ϕ (

P(|X-a|< = 2ϕ(

P(|X-10|<10) = 2ϕ (

2ϕ(2,5) = 2*0,4938 = 0,9876

125. Задано закон розподілу випадкової величини X:

	x			0
	p	0,2	0,2	0,4	0,1	0,1	.

Знайти закон розподілу випадкової величини

M(Y) = 2cos - *0,2 + 2cos - *0,2 + 2cos0 * 0,4 + 2cos+ 2cos * 0,1 = далі замість cos - з таблиці косинусів обираємо число.

130. Із чотирьох студентів КНЕУ, два з яких навчаються на обліково-економічному факультеті, один – на фінансовому та один – на факультеті МЕіМ, банк обирає на роботу лише двох. Ймовірність працевлаштування для кожного студента вважається однаковою. Випадкова величина Х – кількість обраних студентів з фінансового факультету, Y – кількість обраних студентів з факультету МеіМ. Скласти закон розподілу системи (X,Y); знайти закони розподілу X та Y; F(x); F(y); F(x;y). Чи залежні величини X та Y?

Х = 0 – жодного студента не обрали з фін. факультету

Р (Х=0) = 0,5

Х = 1 – обрали студента з фін. факультета

Р (Х=1) = 0,5

Y = 0 - жодного студента не обрали з МЕіМ

Р (Y=0) = 0,5

Y = 1 – обрали студента з МЕіМ

Р (Y=1) = 0,5

1. Знайдемо закон сумісного розподілу системи (X,Y).

p₁₁ = P{X = 0;Y = 0}= 0,5*0,5 = 0,25 ;

p₁₂ = P{X = 1;Y =0}= 0,5*0,5 = 0,25 ;

p₂₁ = P{X =0;Y = 1}= 0,5*0,5 = 0,25 ;

p₂₂ = P{X =1;Y =1}= 0,5*0,5 = 0,25 .

X Y	0	1
0	0,25	0,25
1	0,25	0,25

Складемо закони розподілу одновимірних випадкових величин X i Y

X	0	1
p	0,5	0,5

F(x) =

Y	0	1
p	0,5	0,5

F(y) =

Випадкові величини X i Y — незалежні, тому F(x, y) = F₁(x)F₂(y) подаємо таблицею:

X Y	x ≤ 0	0 < x ≤ 1	x > 1
y ≤ 0	0	0	0
0 < y ≤ 1	0	0,25 = 0,5*0,5	0,5 = 1*0,5
y > 1	0	0,5 = 1*0,5	1 = 1*1

134. Двовимірна щільність має вигляд:

. Обчислити сталу (a).

142. Випадкова величина X має обмежені M(X) та . Використовуючи нерівність Чебишова, оцінити ймовірність того, що

.) ≥ 1 -

144. Імовірність появи випадкової події в кожному з 100 експериментів дорівнює 0,8. Використовуючи нерівність Чебишова оцінити ймовірність того, що .

M(X) = 100*0,8 = 80

D(X) = 100*0,8*0,2 = 1,6

P(|X – 80| < 10) ≥ 1 - = 0,984

145. Імовірність появи випадкової події в кожному з 400 випробувань дорівнює 0,5. Оцінити ймовірність того, що у цих незалежних випробуваннях подія відбудеться від 180 до 220 раз: 1) за допомогою нерівності Чебишова; 2) за допомогою інтегральної теореми Лапласа.

M(X) = np = 400*0,5 = 200

D(X) = npq = 400*0,5*0,5 = 100

P(180<X<220) = P(|X – 200|<20) ≥ 1 -

P₄₀₀(180;220) = ϕ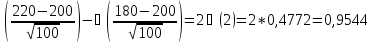

146. Мережа складається з 20 паралельно з’єднаних електричних ламп. Ймовірність того, що за час T лампа буде увімкнена, дорівнює 0,8. За нерівністю Чебишова оцініть ймовірність того, що абсолютна величина різниці між числом увімкнених ламп і середнім числом увімкнених за час T ламп буде : 1) менше чотирьох; 2) не менше чотирьох .

M(X) = np = 20*0,8 = 16

D(X) = npq = 20*0,8*0,2 = 3,2

P(|X – 16| < 4) ≥ 1 - = 0,8

P(|X – 16| > 4) ≤ = 0,2

148. Середнє річне число дощових днів у Київській області дорівнює 30. Оцінити за допомогою нерівності Чебишова ймовірність того, що протягом року в цій місцевості буде менше 50 дощових днів.

Випадкова величина X — річне число дощових днів набуває невід’ємних значень. Її математичне сподівання дорівнює 30.

P(X < 50) ≥ 1 - = 0,4

147. Середня річна кількість опадів в даній місцевості дорівнює 40 см. Використавши нерівність Чебишова оцінити ймовірність того, що в цій місцевості випаде за рік більше 150 см опадів.

Випадкова величина X — річне число дощових днів набуває невід’ємних значень. Її математичне сподівання дорівнює 40.

P(X > 150) ≤

P(X>a) ≤

149. Використовуючи нерівність Чебишова оцінити ймовірність відхилення відносної частоти появи стандартної деталі від імовірності її появи 0,95 не більше ніж на величину ε = 0,02 при контролі 600 деталей.

150. Ймовірність виграшу на кожний лотерейний білет дорівнює 0,2. Придбано 100 білетів. Яка ймовірність того, що відносна частота виграшних білетів знаходиться у межах ? Розв’яжіть задачу: 1) за допомогою нерівності Чебишова; 2) за допомогою інтегральної теореми Лапласа.

M(X) = np = 100*0,2 = 20

D(X) = npq = 100*0,2*0,8 = 16

P(0,1<X<0,3) = P(|X – 20| < 10) ≥ 1 -

P₁₀₀(0,1; 0,3) = ϕ

153. Імовірність виготовлення майстром стандартної деталі дорівнює 0,98. Користуючись нерівністю Чебишова, обчислити скільки деталей потрібно виготовити, щоб з ймовірністю не меншою 0,9 відносна частота виготовлення стандартної деталі відхилялась від її ймовірності на величину не більшу 0,05.

≥ 0,9

n ≥ (7,84/0,1) = 79