

Тольяттинский государственный университет Физико-технический институт
Кафедра «Общая и теоретическая физика»
Потемкина Л.О., Павлова А.П., Леванова Н.Г.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО РЕШЕНИЮ ЗАДАЧ ПО ФИЗИКЕ
3й семестр
Модуль 9
КВАНТОВАЯ ФИЗИКА
Тольятти 2007
Содержание |
|
Условные обозначения..................................................................................................................................................... |
3 |
Занятие №33. Тепловое излучение.................................................................................................................................. |
3 |
Основные формулы..................................................................................................................................................... |
3 |
Примеры решения задач............................................................................................................................................. |
6 |
Занятие №34. Фотоэффект. Волны де Бройля................................................................................................................ |
9 |
Основные формулы..................................................................................................................................................... |
9 |
Примеры решения задач........................................................................................................................................... |
10 |
Занятие №35. Соотношения неопределенностей. Уравнение Шредингера............................................................... |
16 |
Основные формулы................................................................................................................................................... |
16 |
Примеры решения задач........................................................................................................................................... |
18 |
Занятие №36. Физика атомного ядра ............................................................................................................................ |
21 |
Основные формулы................................................................................................................................................... |
21 |
Примеры решения задач........................................................................................................................................... |
23 |
Варианты задач автоматизированной контрольной работы – АКР№9 ...................................................................... |
26 |
2
Условные обозначения
1.ω – циклическая частота;
2.ν – линейная частота;
3.λ - длина волны;
4.R - энергетическая светимость (мощность излучения) тела;
5.Rе - энергетическая светимость абсолютно черного тела (АЧТ);
6.rωT, rλ¸T, rν¸T – спектральная плотность энергетической светимости (испускательная способность тела);
7.RТ – интегральная энергетическая светимость (интегральная излучательность) тела
8.аωT, аνT – спектральная поглощательная (поглощательная) способность тела;
9.T – термодинамическая температура;
10.Tр- радиационная температура;
11.Tц- цветовая температура;
12.Tя – яркостная температура;
13.σ – постоянная Стефана-Больцмана;
14.b – постоянная Вина;
15.f(ω,T) – универсальная функция Кирхгофа;
16.h - постоянная Планка;
17.ħ - постоянная Планка, делённая на 2π;
18.k - постоянная Больцмана;
19.c – скорость света в вакууме.
Занятие №33. Тепловое излучение
Основные формулы
Энергетическая светимость – это поток энергии, испускаемый единицей площади поверхности излучающего тела по всем направлениям (в пределах телесного угла 2π). Энергетическая светимость является функцией температуры.
R = |
dW |
, |
(1) |
|
dS dt |
||||
|
|
|
[ R ] = Дж / ( м2 с ) = Вт / м2.
Спектральная плотность энергетической светимости – это мощность излучения с единицы площади поверхности тела в интервале частот единичной ширины. Спектральная плотность энергетической светимости ( испускательная способность ) является функцией частоты и температуры.
rω T = |
dR |
= |
dWωизл, ω+dω |
, |
(2) |
|
dω |
dt |
|||||
|
|
|
|
[ rω T ] = Дж / м2.
Спектральная поглощательная способность – безразмерная величина, показывающая, какая доля энергии, приносимой за единицу времени на единицу площади поверхности тела падающими на нее электромагнитными волнами с частотами ω, ω+dω , поглощается телом:
3

|
dW погл |
|
|
aω T = |
ω, ω+dω |
. |
(3) |
пад |
|||
|
dW |
|
|
|
ω, ω+dω |
|
|
Спектральная поглощательная способность является функцией частоты и температуры.
Тело, полностью поглощающее падающее на него излучение всех частот аωT ≡ 1 называется абсолютно черным телом.
Тело, для которого аωT ≡ аω = const < 1, называется серым. Закон Кирхгофа:
rω T = f (ω,T ) . aω T
Для любого тела:
RT = ∞∫aω T rω T dω .
0
Для абсолютно черного тела:
Re = ∞∫rω T dω .
0
Для серого тела:
∞
RTC = aω T ∫rω T dω = aω T Re .
0
Закон Кирхгофа описывает только тепловое излучение. Закон Стефана-Больцмана:
Re =σ T 4 .
(4)
(5)
(6)
(7)
(8)
где Re – энергетическая светимость (излучательность) черного тела, σ - постоянная Стефана-Больцмана,
T - термодинамическая температура.
σ = 5,67 * 10-8 Вт/(м2 * К4).
Связь энергетической светимости Re и спектральной плотности энергетической светимости rν ,T ( r λ,T ) черного тела:
Re = ∞∫rν T dν = ∞∫rλ T dλ . |
(9) |
||||
0 |
|
|
0 |
|
|
Энергетическая светимость серого тела: |
|
|
|
|
|
RC = A σ T 4 , |
(10) |
||||
T |
T |
|
|
|
|
где AT – поглощательная способность серого тела. |
|
|
|
||
Закон смещения Вина: |
|
|
|
|
|
λmax = |
b |
|
, |
(11) |
|
T |
|
||||
|
|
|
|
|
|
где λ max – длина волны, соответствующая максимальному значению спектральной плотности энергетической светимости черного тела,
b - постоянная Вина. b = 2,9 · 10-3 м ·К
Зависимость максимальной спектральной плотности энергетической светимости черного тела от температуры:
4

(rλ T )max = C T 5 , |
(12) |
где С = 1,3 · 10 –5 Вт / ( м3 · К 5)
Формула Релея-Джинса для спектральной плотности энергетической светимости черного тела:
r |
= |
2πν2 |
kT , |
(13) |
|
||||
ν , T |
|
c2 |
|
|
|
|
|
|
где k - постоянная Больцмана. k = 1,38 · 10 – 23 Дж / К
Энергия кванта:
ε0 |
= hν = |
hc |
, |
(14) |
|
λ |
|||||
|
|
|
|
где h – постоянная Планка. h = 6,63 · 10 – 34 Дж · с
Формула Планка:
r |
= |
|
2πν2 |
|
|
|
hν |
, |
(15) |
||||
|
c2 |
|
|
|
|
|
|
|
|||||
ν , T |
|
|
|
e |
hν |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
kT |
|
−1 |
|
|
|
|||
r |
= |
2π c2 |
1 |
|
|
. |
(15′) |
||||||
5 |
|
|
|
hc |
|
|
|
|
|||||
λ, T |
|
|
|
|
|
|
|
|
|
||||
|
|
|
λ |
|
e |
|
−1 |
|
|||||
|
|
|
|
λkT |
|
||||||||
Формула Планка для универсальной функции Кирхгофа:
f (ω,T ) = |
=ω3 |
1 |
|
, |
|||
4π2c2 |
|
|
=ω |
|
|
||
|
|
|
|
|
|||
|
|
ekT |
−1 |
||||
|
|
|
|||||
где ħ = 1,05 · 10 – 34 Дж / c
Радиационная температура:
Трад = 4 RσT .
Цветовая температура:
Тцв = λb . max
(16)
(17)
(18)
Яркостная температура – это температура абсолютно черного тела, при которой для определенной длины волны его спектральная плотность энергетической светимости равна спектральной плотности энергетической светимости исследуемого тела:
rλ,Tя = Rλ,T .
Связь между ω иλ:
λ = 2π ωс .
Поглощательная способность:
hc
= ekThc −1 . ekλTя −1
Связь радиационной Tp и истинной T температур:
(19)
(20)
(21)
5
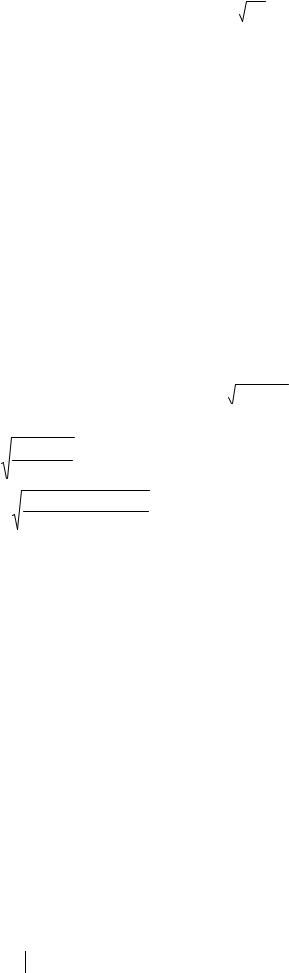
Трад = 4 АТ Т , |
(22) |
где АТ – поглощательная способность серого тела.
Примеры решения задач
Пример №1. Найти температуру Т печи, если известно, что излучение из отверстия в ней площадью S = 6.1 см2 имеет мощность N = 34.6 Вт. Излучение считать близким к излучению АЧТ.
Дано: |
Решение: |
|
|
|
S = 6.1см2 |
По определению: |
|
|
|
N = 34.6 Вт |
|
|
Rэ= W/S·t |
|
Т – ? |
или |
|
|
|
|
|
|
Rэ = N/S |
(1) |
Согласно закону Стефана–Больцмана для АЧТ: |
|
|||
|
|
|
Re =σ T 4 . |
(2) |
Сравнив (1) и (2) получим: |
Т= 4 N /(Sσ). |
|
||
|
|
|
|
|
Проверка единицы измерения: |
|
|
||
[ Т] = К = 4 |
Втм2 К4 |
= К. |
|
|
Втм2 |
|
|
||
|
|
|
|
|
Расчет: T = |
|
34.6 |
=1000 К. |
|
6.1 10−4 5.67 10−8 |
|
|||
Ответ: Т = 1000 К
Пример №2. Температура вольфрамовой спирали 25-ваттной электрической лампочке
T = 2450 К. Отношение ее энергетической светимости к энергетической светимости АЧТ при данной температуре равно k = 0.3. Найти площадь излучаемой поверхности.
Дано: |
Решение: |
N = 25Вт |
Для нечерного тела величина энергетической светимости равна: |
T = 2450К |
Rэ = k1*σ*T4, |
k = 0.3 |
а по определению Rэ' = N/S. |
|
Тогда |
S = ? |
|
|
N/S = k*σ*T4, |
|
S = N/σ*k*T4. |
Проверка единицы измерения: [S] = м2 = Вт*м2*K4/Вт*K4 = м2;
Расчет числового значения: S = 0.4079*10-4 м2 ≈ 0.41см2;
Ответ: S = 0.41 см2
Пример №3. Какую энергетическую светимость Rэ имеет АЧТ, если максимум спектральной плотности его энергетической светимости приходится на длину волны λ = 484 нм?
Дано: Решение:
6

λmax = 484 нм |
Согласно закону Стефана-Больцмана: |
|
Rэ = σ·T4 (1). |
Rэ = ? |
Для нахождения T воспользуемся законом Вина:
λm = C1/T,
отсюда:
T=C1/λ.
Получим:
Rэ = (σ*C14)/λ4.
Проверка единицы измерения:
[Rэ] = Дж/м2·с = Вт/м2·К4 · м4*К4/м4 = Дж/с·м2 ;
Расчет числового результата:
Rэ = (5,67·10-8·2.94·10-12)/(484)4·10-36 = (1020·5.67·2.94)/(484)4 = = 73.5 МВт/м2 Ответ: Rэ = 73.5 МВт/м2.
Пример №4. Абсолютно черное тело имеет температуру T1 = 2900 К. В результате остывания тела длина волны, на которую приходится максимум спектральной плотности энергетической светимости изменилось на ∆λ = 9мкм. До какой температуры T2 охладилось тело?
Дано: |
Решение: |
T1 = 2900 К |
Согласно закону Вина: |
∆λ = 9мкм = 9·10-6 м |
λmax2 = C1/T2, |
|
где T1-начальная, а T2-конечная температура тела; |
T2=? |
|
|
λmax1 = C1/T1 |
Т.к. тело охлаждается, то T2 < T1 , а λmax2 > λmax1;
λmax2 = λmax1+∆λ
И получим:
C1/λmax+∆λ = T2
T2 = C1/(C1/T1)+∆λ = 1/(1/T1)+(∆λ/C1) = C1·T1/(∆λ·T1+C1)
Проверка единицы измерения: [T2] = K= м·К/м = К;
Расчет числового значения: T2 = 290 К;
Ответ: T2 = 290 К.
Пример №5. При нагревании АЧТ длина волны, на которую приходится максимум спектральной плотности энергетической светимости изменилась от 690 до 500 нм. Во сколько раз увеличилась при этом энергетическая светимость тела?
Дано: |
Решение: |
λ1 = 690 нм |
По закону Стефана – Больцмана для АЧТ имеем: |
|
λ2=500 нм |
|
=σ T1 |
|
RЭ1 |
|
|
|
4 |
|
|
|
Rэ2 / Rэ1 = ? |
4 |
|
|
|
=σ T2 |
|
RЭ2 |
|
где Т1 и Т2 – температуры соответствующие значениям λ1 и λ 2. Значения температур найдем из 1-го закона Вина:
T1=С1/λmax1
T2=C1/λmax2
7

Получим:
Rэ1 = σ ·С14/λmax14;
Rэ2 = σ ·С14/ λmax24;
Найдем отношение:
Rэ2/Rэ1=σ·С14·λmax14 / λmax24· σ·C14=(λmax1/λmax2)4
Проверка единицы измерения: [Rэ2/ Rэ1]=1 (безразмерная величина) Расчет числового значения: Rэ2/Rэ1=3.63 (рад)
Ответ: Rэ2/Rэ1=3.63 рад.
Пример №6. Исследования спектра излучения Солнца показывают, что максимум спектральной плотности излучательности соответствует длине волны λ = 500 нм. Принимая Солнце за абсолютно черное тело, определить: 1) излучательность Re Солнца; 2) поток энергии Ф, излучаемый Солнцем; 3) m массу электромагнитных волн (всех длин), излучаемых Солнцем за 1 с.
Дано:
λ = 500 нм t = 1 c
Re - ? Ф - ? m - ?
Решение:
1. Излучательность Re АЧТ выражается законом Стефана-Больцмана: Re = σ * T4.
Температура излучающей поверхности может быть определена из закона смещения Вина:
λ max = b / T.
Выразив отсюда температуру Т и подставив ее в закон Стефана-Больцмана, получим: Re = σ ( b / λ max )4.
Расчет: Re = 64 МВт / м2
2. Поток энергии Ф, излучаемый Солнцем, равен произведению излучательности Солнца на площадь S его поверхности:
Ф = Re S
или
Ф = Re 4 π r2,
где r – радиус Солнца. Подставив в формулу значения π, r и Re и произведя вычисления получим:
Ф = 3,9 10 26 Вт.
3. Массу электромагнитных волн (всех длин), излучаемых Солнцем за время t = 1 c, определим применив закон пропорциональности массы и энергии Е = m с2. Энергия электромагнитных волн, излучаемых за время t, равна произведению потока энергии Ф (мощности излучения) на время:
Е = Ф t.
Следовательно,
Ф t = m с2,
Откуда
m = Ф t / с2.
Расчет: m = 4 10 12 г.
Ответ: m = 4 10 12 г.
8
