
физика метод указания к решению задач модуль 6
.pdf
Тольяттинский государственный университет Физико-технический институт
Кафедра “Общая и теоретическая физика“
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО РЕШЕНИЮ ЗАДАЧ ПО ФИЗИКЕ
2й семестр
Модуль 6
ЯВЛЕНИЯ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ. ПОЛЕ В ВЕЩЕСТВЕ
Потемкина Л.О., Павлова А.П., Леванова Н.Г.
2007
УДК 537(075.8)
ББК 22.33
П 64
Потемкина Л.О., Леванова Н.Г., Павлова А.П. Методические указания для практической аудиторной и самостоятельной работы студента по решению задач 2 семестр, Тольятти: ТГУ, 2006.
Данное пособие предназначено для организации работы студентов во втором семестре обучения при модульном изучении курса «Физика» на практических занятиях. В нем содержание практических занятий соответствует разбиению курса физики на три модуля. Пособие составлено в соответствии с действующей программой по курсу физики для втузов. Подробно расписано каждое практическое занятие по темам. В заключении темы приводится описание автоматизированной контрольной работы и примерный ее вариант. Пособие составлено в двух частях: механика и термодинамика. В каждый раздел включено достаточное количество задач, приводятся основные законы и формулы, даются методические указания, необходимые для решения задач по данной тематике и примеры решения типовых задач.
© Тольяттинский государственный университет, 2006.
ОГЛАВЛЕНИЕ |
|
Явления электромагнитной индукции............................................................................................. |
4 |
Занятия № 21-22 (4 часа)............................................................................................................... |
4 |
Тема: Явление электромагнитной индукции. Работа по перемещению |
|
проводника с током в магнитном поле. Индуктивность. .................................. |
4 |
Поле в веществе................................................................................................................................ |
18 |
Занятие № 23................................................................................................................................ |
18 |
Тема: Электростатическое поле в диэлектрике.................................................. |
18 |
Занятие № 24................................................................................................................................ |
31 |
Тема: Магнитное поле в веществе............................................................................. |
31 |
Вариант контрольной работы – АКР № 6...................................................................................... |
45 |

Явления электромагнитной индукции
Занятия № 21-22 (4 часа). Явление электромагнитной индукции. Работа по перемещению проводника с током в магнитном поле. Индуктивность.
Основные формулы
1. Магнитный поток, пронизывающий площадку S:
|
ΦB = ∫BG dSG =∫Bn dS |
(1) |
|
|
s |
s |
|
G |
Bn |
=| B | cosα , |
(2) |
G |
|
|
|
где α = (B, n) |
|
|
|
2. Работа перемещения замкнутого контура с током в магнитном поле:
A = I Φ,
где Ф – приращение магнитного потока, пронизывающего поверхность, ограниченную контуром, I – сила тока.
3. Закон Фарадея для электромагнитной индукции:
Ei = −N ddtФ = − ddtΨ
или
(3)
(4)
< Ei > = −N |
Ф |
, |
(4`) |
|
t |
||||
|
|
|
где Ei – электродвижущая сила индукции, N – число витков контура,
Ψ = NΦ |
(5) |
Ψ– потокосцепление.
4.Если проводник длиной L движется со скоростью υ в однородном магнитном поле, то
разность потенциалов U на концах проводника равна:
U = BLυsinα |
(6) |
где α – угол между направлениями векторов скорости υ и магнитной индукции В.
5. Если рамка имеет N витков, а площадь рамки S, то при вращении рамки с угловой скоростью ω в однородном магнитном поле с индукцией В в рамке возникает электродвижущая сила индукции Еi, равная:
Ei = NBωS sin(ωt) |
(7) |
или, если ω = 2πn , то |
|
Ei = 2πтNBS sin(2πnt), |
(7`) |

|
|
|
|
|
|
|
→ |
→ |
где 2πnt – мгновенное значение угла между вектором В и вектором нормали n к плоскости |
||||||||
рамки. |
|
|
|
|
|
|
|
|
6. Мгновенное значение электродвижущей силы самоиндукции, возникающей в контуре |
||||||||
при изменении силы тока в нем: |
|
|
||||||
|
|
|
Ei = − |
LdI |
|
|
(8) |
|
|
dt |
|
||||||
|
|
|
|
|
|
|||
или среднее значение ЭДС самоиндукции равно: |
|
|
||||||
|
|
|
< Ei >= − |
L I |
, |
(8`) |
||
|
t |
|||||||
|
|
|
|
|
|
|
||
где L – индуктивность контура. |
|
|
||||||
7. |
Потокосцепление контура: |
|
|
|||||
|
|
|
ψ = LI |
|
(9) |
|||
|
|
|
|
|
|
|
|
|
8. |
Индуктивность соленоида: |
|
|
|||||
|
|
|
L = μμ0n02V |
|
(10) |
|||
где n0 |
= |
N |
– число витков, приходящихся на единицу длины соленоида, V – объем соленоида, |
|||||
|
||||||||
|
|
l |
|
|
||||
μ– магнитная проницаемость сердечника соленоида, μ0 – магнитная постоянная.
9.Для расчета индукции магнитного поля и индуктивности соленоида и тороида с ферромагнитным сердечником из железа можно использовать график зависимости B = f (H ).
μ = B H .
μ0
10. Сила экстратока при размыкании цепи:
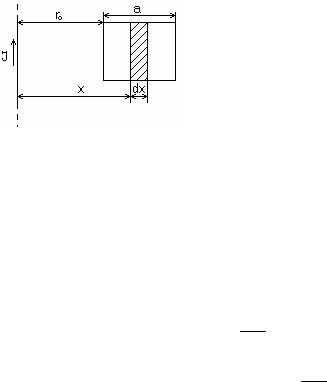
It = I0 exp(− Rt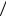 L)
L)
11. Сила экстратока при замыкании цепи:
It = I0 [1−exp(− Rt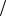 L)]
L)]
12. Заряд, протекший в контуре при изменении магнитного потока через него:
Q = − Rψ
или
(11)
(12)
(13)
(14)
|
R ∫ |
|
R |
|
|
||
Q = |
1 |
|
dψ = |
1 |
(ψ2 |
−ψ1 ) |
(14`) |
|
|
||||||
13. Для преобразования механической энергии в электрическую используются генераторы (электрические машины). При работе генератора в соответствии с законом сохранения и превращения энергии:
N = PЭЛ |
(15) |
или
N = EI |
(15`) |
где Е – ЭДС генератора, I – сила тока в цепи якоря.
14.Для генератора с постоянными магнитами Е определяется по формуле (7).
15.Напряжение U на зажимах генератора равно:
U = E-IR , |
(15``) |
где R – сопротивление якоря.
16. Для преобразования электрической энергии в механическую служат электрические машины, называемые электродвигателями. При работе электродвигателя электрическая мощность, развиваемая источником питания, частично расходуется на нагревание цепи, а частично на вращение якоря. Если Eист – ЭДС источника питания, I – сила тока в цепи, R – сопротивление цепи, N – механическая мощность, развиваемая двигателем, то
|
IEист = I 2 R + N . |
(16) |
||||
17. |
С другой стороны механическая мощность равна: |
|
||||
|
N = Mω = IEi , |
(17) |
||||
где М – вращающий момент на валу мотора, ω – угловая скорость вращения якоря. |
|
|||||
18. |
ЭДС индукции, возникающая в обмотке якоря, Ei, равна: |
|
||||
|
Ei = Eист − IR |
(18) |
||||
19. |
Коэффициент трансформации равен: |
|
|
|
|
|
|
k = |
n1 |
= |
ε1 |
, |
(19) |
|
n2 |
|
||||
|
|
|
ε2 |
|
||
где n1 – число витков в первичной обмотке трансформатора; n2 – во вторичной, ε1 и ε2 – ЭДС самоиндукции и индукции, возникающие в первичной и вторичной обмотках.
20. Если падение напряжения в первичной цепи трансформатора ничтожно мало по сравнению с напряжением U1, подаваемым на трансформатор, то можно считать:
|
|
|
|
|
E1 |
=U1 |
|
|
|
(20) |
||||||
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E2 |
=U 2 , |
|
|
|
(21) |
|||||||
|
|
|
|
n1 |
|
= |
|
U1 |
. |
|
|
(22) |
||||
|
|
|
|
n2 |
|
|
|
|||||||||
|
|
|
|
|
U 2 |
|
|
|
|
|||||||
21. Если во вторичной цепи сила тока велика, то падением напряжения на вторичной |
|
|||||||||||||||
обмотке пренебречь нельзя, и теперь: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E2 = U 2 R2 |
|
|
(23) |
||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n1 |
= |
|
|
|
|
|
U1 |
|
|
, |
(24) |
||||
|
|
U |
|
|
|
r |
||||||||||
|
n |
2 |
|
|
2 |
+ I |
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||

где I2 – сила тока во вторичной цепи, r2 – ее сопротивление.
Методические указания к решению задач
Фундаментальным законом явления ЭМИ является закон Фарадея: εi = − ddtψ .
1. При решении задач на расчет величины электромагнитной индукции, удобно пользоваться следующими рекомендациями:
a)Анализируя условия задачи, необходимо, прежде всего, установить причины изменения магнитного потока, связанного с контуром, и определить, какая из величин: B, S или
α, входящих в выражение для ФB, изменяется с течением времени. После этого нужно записать основное расчетное соотношение (4) или (4’). Если в задаче рассматривается поступательное движение прямого проводника, то ЭДС индукции определяют по формуле (6), вытекающей из закона электромагнитной индукции.
b)Затем выражение для ФB надо представить в развернутом виде. Для этого выбирают два момента времени t1 и t2 и для каждого из них определяют потоки Ф1 и Ф2 связанные с
данным контуром. Изменение магнитного потока за время t =t2 −t1 в зависимости от условия задачи будет равно Ф = (В2 − В1)S cosα , если изменяется индукция магнитного поля, в
котором находится контур, или Ф = ВS(cosα2 −cosα1) , если изменяется положение рамки в поле, или, наконец, Ф = В S cosα , где S −изменение площади контура, описанного в пространстве движущимся проводником.
c) Далее надо подставить выражение для Ф в исходную формулу закона электромагнитной индукции и, записав дополнительные условия, решать полученные уравнения совместно относительно искомой величины. Обычно наибольшие затруднения возникают при расчете электрических цепей, содержащих аккумуляторы, когда на одном из участков цепи возникает ЭДС индукции, вызванная движением проводника в магнитном поле. Решение таких задач нужно начинать с определения полярности и модуля этой ЭДС индукции, после чего задача сведется к расчету обычной цепи постоянного тока с несколькими источниками ЭДС, соединенными между собой последовательно или параллельно.
2. Возможен также другой способ решения задач на явление электромагнитной индукции, когда величина ЭДС находится не через изменение магнитного потока, а непосредственно как работа сторонней силы (чаще всего силы Лоренца).
3. Решение задач о работе электрических машин постоянного тока основано на составлении уравнения закона сохранения и превращения энергии. В простейших случаях его достаточно для нахождения искомой величины; в более сложных задачах к уравнению энергетического баланса необходимо добавить вспомогательные уравнения, позволяющие представить в развернутом виде ту или иную величину, входящую в основное уравнение. Обычно для этого нужно использовать формулы (15), (16),(17).
Примеры решения задач
Пример № 1
В плоскости квадратной рамки с омическим сопротивлением R и стороной а расположен на расстоянии r0 от рамки прямой бесконечный проводник (см. рис. 1). Сила тока в проводнике изменяется по закону I = bt3, где b>0 и b = const. Проводник параллелен одной из сторон рамки. Определить: 1) магнитный поток, пронизывающий площадь рамки; 2) ЭДС индукции, наведенную в рамке; 3) силу тока в рамке в момент времени t.
Дано: |
Решение: |
||
r0 |
|
Сделаем рисунок: |
|
a |
|
|
|
|
|
|
|
I=bt3 |
|
|
|
|
|
|
|
Ф = ? |
|
|
|
εi |
= ? |
|
|
It |
= ? |
|
|
|
Рис.1 |
||
|
|
|
|
Вследствие изменения силы тока в проводнике магнитный поток, пронизывающий плоскость рамки, изменяется и в ней возникает индукционный ток. Рамка находится в неоднородном магнитном поле. Поэтому для расчета потока применим метод ДИ – дифференцирования и интегрирования. Разделим площадь рамки на столь узкие полоски шириной dx, чтобы в пределах каждой полоски магнитное поле можно было считать
однородным. По закону Био-Савара-Лапласа B = μ2π0xI . Выразим элементарный магнитный
поток сквозь узкую полоску шириной dx: dΦ = Badx = adx μ2π0xI .
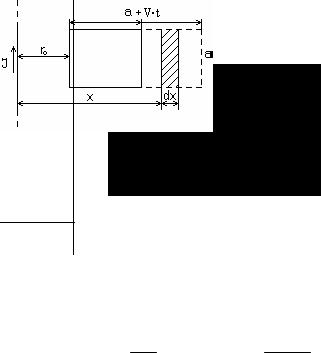
Интегрируя это выражение по х от r0 до (r0 + а), получим:
r0 +a |
Iadx |
|
μ0bt |
3 |
a |
r0 +a |
dx |
|
μ0abt |
3 |
+a |
|
|
|
Φ = ∫ μ0 |
|
|
∫ |
|
r0 |
|
|
|||||||
2πx |
= |
2π |
|
|
x |
= |
2π |
ln |
|
|
|
; |
||
|
|
|
r |
|||||||||||
r |
|
|
|
|
|
r |
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
dΦ |
|
2 |
|
|
μ0b |
|
+а |
|
||||
|
Ei = − |
|
|
|
r0 |
|
|||||||||||
По закону Фарадея найдем ЭДС индукции: |
|
|
= 3t |
|
a |
|
ln |
|
|
. |
|||||||
dt |
|
|
2π |
|
r |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
εi |
t |
2 |
aμ0b |
|
|
+ а |
|
|
|
|
|
||||||
|
r0 |
|
|
|
|
|
|||||||||||
А сила тока из закона Ома равна: I = R = 3 |
|
|
ln |
|
|
|
|
; |
|
|
|
|
|||||
|
2πR |
|
|
r |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||
Проверка размерности: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
[Ф] = 1Вб = 1Тл м2 = |
Дж |
|
= |
Гн |
А м = В·с = |
|
Дж |
; |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
А |
м |
|
А |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
[εi] = |
Гнс2Ам |
= |
ВсА |
=1В; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
мс3 |
|
|
сА |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
[I] = |
|
В |
=1А. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Ом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
μ0abt |
3 |
|
|
+ а |
|
|
2 |
|
μ0b |
|
|
|
|
|
t |
2 |
aμ0b |
|
+ а |
|
|||||||
Ответ: Φ = |
|
|
r0 |
|
; εi = 3t |
a |
|
r0 + а |
|
; I = 3 |
|
r0 |
|
||||||||||||||||||
|
|
|
ln |
|
|
|
|
|
|
ln |
|
|
|
|
|
ln |
|
|
. |
||||||||||||
|
2π |
|
|
r |
|
|
2π |
|
r |
|
2πR |
|
r |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
|
||||
Пример № 2
dΦ = Bds ; B = μ2π0xI ; dΦ = Βadx = μ02Iadxπx ; х0 = а; xt = a +Vt
|
|
|
μ |
|
Ia a+Vt dx |
|
μ |
|
|
Ia |
|
|
|
a +Vt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Φ = |
|
0 |
|
|
∫ |
|
|
|
= |
|
|
0 |
|
|
|
ln |
|
|
|
|
|
, и далее Э.Д.С. индукции: |
|
|||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
a |
|
|
||||||||||||||||||||||||||||
|
|
|
2π |
|
a |
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
ε |
|
|
|
dФ |
|
|
d |
μ |
|
|
Ia |
|
|
|
a +Vt |
|
|
|
|
μ |
0 |
Ia2V |
|
|
|
|
|
|
||||||||||||||
|
= − |
|
|
|
= − |
|
|
|
|
0 |
|
|
|
ln |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
. |
|
|
|||||||||
|
|
dt |
dt |
|
|
|
|
|
|
|
a |
|
2π |
(a +Vt + r )(V + r |
) |
|
||||||||||||||||||||||||||
|
i |
|
|
|
|
|
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
Ответ:ε |
|
= − |
dФ |
= − |
d |
|
|
μ |
|
|
Ia |
|
a +Vt |
= |
|
|
μ |
0 |
Ia2V |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
ln |
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||||||||||||
|
dt |
dt |
|
|
|
|
|
a |
|
2π |
(a +Vt + r )(V + r ) |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
2π |
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
Пример № 3
Прямой бесконечный ток I1 и прямоугольная рамка длиной b и шириной A с током I2
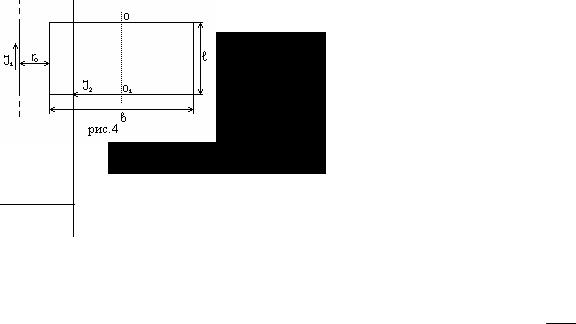
расположены в одной плоскости так, что сторона рамки l параллельна прямому току и отстоит от него на расстоянии r0 = 0,1 b. Определить: какуюработу необходимо совершить для того,
чтобы повернуть рамку на угол ϕ1 = 90° относительно оси 001, параллельной прямому току и проходящей через середины противоположных сторон (b) рамки.
Дано: Решение:
I1
I2
B
A
r
При повороте рамки на угол 90° магнитный поток Ф2 (в конечном положении)
А = ?
равен 0. В начальный момент вращения В перпендикулярен плоскости рамки,
направлен так, что мы видим его хвостик. По определению: А=I2 Ф. Ф = Ф2 – Ф1 = –Ф1. Так как Ф2=0, то работа А будет отрицательна, и надо найти Ф1. Магнитное поле создается
бесконечным прямолинейным током I1. Его поле является неоднородным: В = μ2π0 Ix1 . Для
расчета Ф1 применим метод ДИ. Разделим площадь рамки на столь узкие полоски шириной dx, чтобы в пределах каждой такой полоски магнитное поле можно было считать однородным.
Тогда каждая полоска имеет площадь dS = A dx, а элементарный магнитный поток через эту
полоску равен:
dΦ = BdS = μ0 I1 ldx .
2πx
Полный магнитный поток сквозь рамку равен:
Φ1 = |
|
dФ = |
μ |
|
I l 0,5b dx |
= |
μ |
|
I l |
ln5 ; |
||
|
|
0 |
1 |
|
|
0 |
1 |
|||||
∫ |
2π 0∫,1 x |
2π |
||||||||||
|
|
|
|
|||||||||
