Тренинг по модулю «Кратные интегралы»

Вопросы теории (двойной интеграл)

1. Если D ограничена слева и справа прямыми х = а и х = b (a<b), а снизу и сверху – непрерывными кривыми у = φ1(х) и у = φ2(х) (φ1(х) < φ2(х)), то двойной интеграл вычисляют по формуле

1.по переменной у;

2.по любой переменной

3.по переменной х.

3. Площадь области D, находится по формуле

1)S = ∫∫dxdy

D

2)S = ∫∫ f (x, y)dxdy

D

3)S = ∫∫ Ddxdy

f( x, y)

4.Если f(х,у) > 0 в области D, то двойной интеграл ∫∫ f ( x, y )dxdy равен

D

1.площади области D

2.массе тела, при условии что f(х,у) – плотность в каждой точке

3.объему цилиндрического тела

Вычисление двойного интеграла

1. Вычислить ∫∫ x ln ydxdy , если область D – прямоугольник 0 ≤ х ≤ 4; 1 ≤ у ≤ е;

D

1.16

2.4

3.12

4.8е

5.8

27

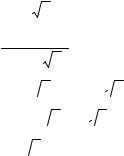
2. Вычислить ∫∫(cos2 x + sin2 y )dxdy , если область D – квадрат 0 ≤ х ≤ π/4; 0 ≤ у ≤ π/4

D

1.π2

2.π2/2

3.π2/4

4.π2/16

5.4π2

3.ab(2 3 − ln(2 + 3)

4.ln(2 + 3) − 2 3

5.ab2 3

Связь полярной и декартовой систем координат

1.Каким соотношением связана переменная х в декартовой и полярной системах координат?

1.r sinϕ

2.rtgϕ

3.r cos2 ϕ

4.r cosϕ

5.r sin2 ϕ

2.Каким соотношением связана переменная у в декартовой и полярной системах координат?

1.rcos φ

2.rcos2 φ

3.rsin2 φ

4.rtg φ

5.rsin φ

28

3.В полярной системе координат двойной интеграл имеет вид

1)∫∫ f (cosϕ,sinϕ )rdrdϕ

D

2) ∫∫ f (sinϕ ,cosϕ )rdrdϕ

D

3) ∫∫ f (r cosϕ ,r sinϕ )rdrdϕ

D

4) ∫∫ f (r sinϕ ,r cosϕ )rdrdϕ

D

5)∫∫ f (r cosϕ , r sinϕ )drdϕ

D

4.В полярной системе координат двойной интеграл имеет вид

1)∫∫ f (r sinϕ ,r cosϕ )rdrdϕ

D

3) ∫∫ f (r cosϕ ,r sinϕ )drdϕ

D

4) ∫∫ f (sinϕ ,cosϕ )rdrdϕ

D

5)∫∫ f (r sinϕ, r cosϕ )drdϕ

D

Связь цилиндрической и сферической систем с декартовой системой координат

1. Координата точки х связана в цилиндрической и декартовой системах координат соотношением

1.x = rsin φ

2.x = cos φ

3.x = x

4.x = sin φ

5.x = rcos φ

2.Координата точки у связана в цилиндрической и декартовой системах координат соотношением

1.у = rcos φ

2.у = sin φ

3.у = у

4.у = rsin φ

5.у = cos φ

29

3.Координата точки z связана в цилиндрической и декартовой системах координат соотношением

1.z =z

2.z = rsin φ

3.z = φ cosr

4.z = sin φ

5.z = rcos φ

4.Координата точки х связана в сферической и декартовой системах координат соотношением

1.х =ρsinφ sinθ

2.х =ρcosφ

3.х =ρcosθ

4.х =ρcosφ sinθ 5). х =ρsinφ cos θ

2. Вычислить в полярной системе координат ∫∫ x2 + y2 dxdy , если D – I четверть круга

D

x2 + y2 ≤ a2

1.π6

2.π6a3

3.a3

6

4.πa2

6

5.a6

30

3. Вычислить в полярной системе координат ∫∫( 3 y − 2x )dxdy , если D: x2 + y2 ≤ 16

D

1.64π/3

2.64

3.64π

4.0

5.3π /64

4.Вычислить площадь фигуры, ограниченной кривой y = x3 , прямой у = 8 и осью ОУ

Вопросы теории (тройной интеграл)

1.Тройной интеграл обозначается

1)∫∫∫ f (x, y)dxdydz

V

2) ∫∫∫ f (x, y, z)dxdy

V

3) ∫∫∫ f (x, y, z)dxdydr

V

4) ∫∫∫ f (x, y, z)dxdydz

V

5) ∫∫∫ f (x, y)dxdy

D

2. Вычисление тройного интеграла ∫∫∫ f ( x, y,z )dxdydz начинается по переменной

V

1.х;

2.у;

3.z;

4.по любой.

3.Какое из свойств тройного интеграла верно?

1) ∫∫∫cf (x, y, z)dxdydz = c∫∫∫ f (x, y, z)dxdydz

V V

31

2) ∫∫∫cf (x, y, z)dxdydz = ∫∫∫ f (x, y, z)cdxdydz

V V

4.Объем тела вычисляется по формуле…

1)∫∫∫ f (x, y, z)dxdydz

(x, y, z)dxdydz

4) ) ∫∫∫xdxdydz

v

5) ∫∫∫xf (x, y, z)dxdydz

v

4. Координата центра тяжести тела V по оси ОХ находится по формуле

Вычисление тройного интеграла

dxdydz

1. Вычислить в сферических координатах ∫∫∫V 1 + ( x2 + y 2 + z2 )3 / 2 ,

где V шарx2 + y2 + z2 ≤ 1

1.2ln 2

3

2.4π ln 2

3

3.43π

4.3π ln 2

4

32

5. 4π ln 2

3

2. Вычислить в сферических координатах ∫∫∫ x2 dxdydz ,

V

где V шар x2 + y2 + z2 ≤ R2

1.2R4π

3

2.4R4π

3

3.43π

4.3R4

4

5.4R4π

2

3. Вычислить ∫∫∫ zdxdydz , где V – область, ограниченная верхней частью конуса

V

x2 + y2 = z2 и плоскостью z = 1

1) 3π ln 2

4

2)4π ln 2

3

3)π ln 2 3

4)π ln 2 4

33

Уважаемые студенты, если вы испытываете затруднения при выполнении тренинговых заданий, обращайтесь, пожалуйста, на образовательный портал, задавая вопросы на форуме или в часы индивидуальных консультаций.

34