
метод указания по решению задач
.pdf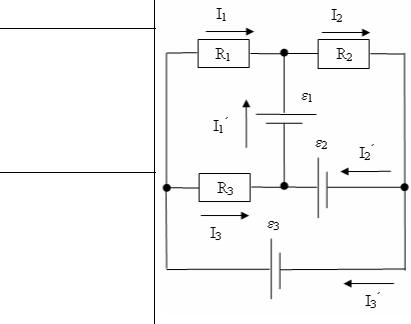
|
1 |
1 |
1 |
− 1 |
|
|
|
||||
= |
2 |
− 4 |
0 |
0 |
= 96 |
|
2 |
0 |
− 4 |
0 |
|
|
0 |
0 |
4 |
2 |
|
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
− 1 |
|
|
|
|
|
|
|
|||||||||
I2 = |
2 |
6 |
0 |
0 |
= 0 ; I3 = |
2 |
− 4 6 |
0 |
|
|
= −96 |
|
|
2 |
10 |
− 4 |
0 |
|
2 |
0 |
10 |
0 |
|
|
|
|
0 |
0 |
4 |
2 |
|
0 |
0 |
0 |
2 |
|
|
|
Отсюда: I2 = 0; I3 = -1A.
Знак «-» у значения I3, свидетельствует о том, что при произвольном выборе направлений токов, направление тока I3 было указано противоположно истинному.
Ответ: I2 = 0; I3 = -1A; ток I3 течет от узла В к узлу А.
Пример № 5
На рисунке ε1 = 10 В, ε2 = 20 В, ε3 = 40 В, а сопротивления R1=R2=R3=R=10 Ом. Определите силу токов, протекающих через сопротивления ( I ) и через источник ЭДС ( I’ ). Внутреннее сопротивление источников ЭДС не учитывать.
Дано:
ε1 = 10 В ε2 = 20 В ε3 = 40 В
R1=R2=R3=R=10 Ом.
I1, I2, I3 - ?
I1’, I2’, I3’ - ?
Решение:
Выберем направления токов.
I ' |
= I |
|
+ I |
|
, |
|
I R |
= ε |
|
− ε |
|
, |
|
3 |
|
1 |
|
3 |
, |
|
|
|
|
||||
I1 + I1' |
= I2 |
; |
1 3 |
|
3 |
|
2 |
|
|
||||
|
+ I2' |
= I1' |
, |
I1 R1 + I2 R2 = ε 3 , |
|
||||||||
I3 |
|
|
= ε 2 + ε 1 |
; |
|
||||||||
|
|
' |
|
' |
|
|
I2 R2 |
|
|||||
I2 |
= I2 |
+ I3 ; |
|
|
|
|
|
|
|
|
|||
I3 10 = 20, |
|
|
|
I2 10 = 30, |
I1 10 + 3 10 = 40; |
||||||||
I3 = 2 A, |
|
|
|
I2 = 3 A, |
|
|
I1 = 1 A; |
||||||
21
I3’ = 3 A, |
I2’ = 0, |
|
I1’ = -2 A, |
I1’ направлен в сторону, противоположную первоначально выбранной. |
|||
Ответ: |
I1 = 1 A; |
I2 = 3 A, |
I3 = 2 A, |
|
I1’ = -2 A, |
I2’ = 0, |
I3’ = 3 A. |
Пример № 6
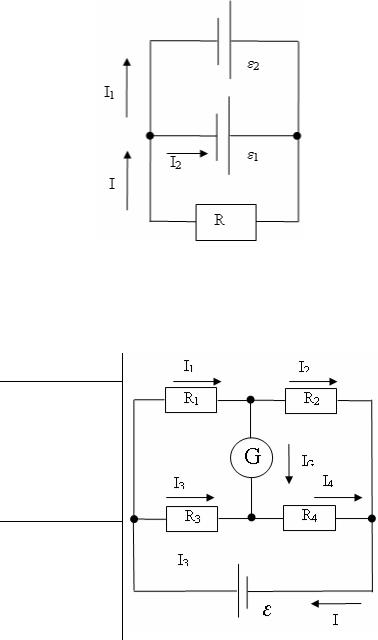
Два источника тока ЭДС ε1 = 2 В и ε2 = 1,5 В и внутренними сопротивлениями
r1 = 0,5 Ом и r2 = 0,4 Ом включены параллельны сопротивлению R = 2 Ом. Определите силу тока через это сопротивление.
Дано: |
Решение: |
||||
|
I = I1 + I 2 , |
||||
ε1 = 2В |
|||||
ε2 = 1,5 В |
IR + I1r1 = ε 1 , |
||||
r1 |
= 0,5 Ом |
IR + I 2r2 = ε 2 , |
|||
r2 |
= 0,4 Ом |
I = |
ε 1r2 + ε 2 r1 |
||
|
|
. |
|||
R = 2 Ом |
Rr1 + r1r2 + Rr2 |
||||
|
|
Ответ: I = 0,775 А. |
|||
I - ? |
|||||
|
|
|
|||
|
|
|
|
|
|
Пример № 7
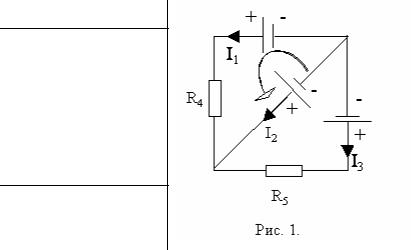
На рисунке ε = 2 В, R1 = 60 Ом, R2 = 40 Ом, R3 = R4 = 20 Ом и RG = 100 Ом. Определить силу тока IG через гальванометр.
Дано:
ε = 2 В
R1 = 60 Ом
R2 = 40 Ом
R3 = R4 = 20 Ом RG = 100 Ом
IG - ?
Решение:
22
I = I1 + I3 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
= I2 |
+ IG |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
+ I4 |
= I, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
+ IG = I4 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
I3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
I1R1 + I2 R2 |
= ε , |
|
|
6I1 |
+ 4I2 |
= 0,2, |
|
|
6I1 + 4(I1 − IG ) |
= 0,2, |
|||||||||
|
|
|
= ε , |
; |
|
+ 2I4 |
= 0,2, |
;→ |
|
|
|
|
|
= 0,2, ; |
|||||
I3 R3 + I4 R4 |
2I3 |
2(I4 − IG ) + 2I4 |
|||||||||||||||||
|
|
|
|
+ I4 R4 = ε ; |
|
+ 10IG + 2I4 |
= 0,2; |
|
|
+ 10IG + 2I4 = 0,2; |
|||||||||
I1R1 + IG RG |
|
6I1 |
|
6I1 |
|||||||||||||||
10I1 − 4IG = 0,2 → I1 |
= |
0,2 + 4IG |
, |
|
|
4I 4 − 2IG = 0,2 → I4 |
= |
|
0,2 + 2IG |
|
, |
||||||||
|
|
4 |
|
||||||||||||||||
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|||
6I1 +10IG + 2I 4 , |
|
|
0,2 + 4IG |
0,2 + 2IG |
|
|
|||||||||||||
|
|
6 |
|
|
|
+ 10IG + 2 |
|
|
|
= 0,2 , |
|
||||||||
|
|
|
10 |
|
|
4 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1,2 + 24IG + 100IG + 1+ 10IG = 2 , |
|
|
|
|
134IG = −0.2 |
|
|
|
IG = -1,49 10-3 A. |
||||||||||
Ответ: IG = -1,49 мA, направлен в сторону, противоположную первоначально выбранной.
Пример 8
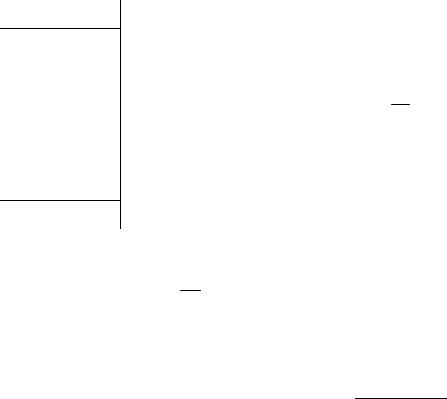
Определить силу токов, текущих в ветвях, если
E1 = 1В, E2 = 2В, E3 = 3В, r1 = 1 Ом, r2 = 0,5 Ом, r3 = 1/3 Ом, R4 = 1 Ом, R5 = 1/3 Ом. (см. рис. 11).
Анализ:
Физическая система - электрическая цепь, в которой имеется несколько различных источников тока. Найти результирующую ЭДС невозможно, и, следовательно, нельзя применить закон Ома для замкнутой цепи. В этом случае электрическая цепь может быть рассчитана с помощью правил Кирхгофа.
Дано:
E1 = 1В, E2 = 2В, E3 = 3В, r1 = 1 Ом,
r2 = 0,5 Ом, r3 = 13 Ом, R4 = 1 Ом, R5 = 13 Ом
I1,I2, I3 = ?
Решение:
Сначала необходимо выбрать (произвольно) направления тока в ветвях. Выберем их так, как показано на рисунке. Если мы ошиблись в выборе направления какого-нибудь тока, то в
23
окончательном решении величина этого тока получится отрицательной, если же случайно выбрано правильное направление тока, то его величина будет положительной.
Применим первое правило Кирхгофа. Оно справедливо для узлов электрической цепи. В данной схеме узлов два: точки А и С. Для узла А по первому правилу Кирхгофа получим: I1 + I2 + I3 = 0. Для узла С первое правило Кирхгофа ничего нового не дает. Применим второе правило Кирхгофа. Оно справедливо только для замкнутых контуров. В данной схеме их три: АВСА, АСDА, АВСDА. Рассмотрим контур АВСА. В этом контуре имеется две ЭДС (Е1 и Е2), три резистора (r1, r2, R4) и два тока (I1 и I2). Для применения второго правила Кирхгофа необходимо выбрать (произвольно) условно-положительное направление обхода контура. Оно необходимо для определения знаков ЭДС и токов. Если направления ЭДС или тока совпадают с направлением обхода контура, то их считают положительными. В противном случае ЭДС или ток считают отрицательными.
Выберем за положительное направление обхода контура АВСА направление против часовой стрелки; ЭДС Е1 направлена против часовой стрелки следовательно, ее считаем положительной; ЭДС Е2 направлена по часовой стрелке (т.е. против направления обхода контура); следовательно, она войдет в уравнение второго правила Кирхгофа со знаком минус. Ток I1 проходит через резисторы r1 и R4, и его направление совпадает с направлением обхода контура. Ток I2 проходит через резистор r2 и направлен против направления обхода. Следовательно, ток I1 положителен, ток I2 отрицателен. По второму правилу Кирхгофа для контура АВСА получаем: E1 − E2 = I1 (r1 + R4)− I 2r2 (1).
Если выбрать за положительное направление обхода этого контура направление по часовой стрелке, то по второму правилу Кирхгофа найдем:
− E1 + E2 = I1 (r1 + R4)+ I 2r2 .
Получено уравнение (1), умноженное на (-1). Очевидно, что эти уравнения эквивалентны. Таким образом, сущность второго правила Кирхгофа не зависит от произвольного выбора направления обхода контура.
Рассмотрим контур АСDА. Выберем за положительное направление обхода этого контура направление против часовой стрелки. Применяя второе правило Кирхгофа,
получим: E2 − E3 = I 2r2 − I 3(r3 + R5)(2).
Система уравнений (1) - (2) является замкнутой. Задача физически решена. Решая полученную систему уравнений, находим: I1 = - 85 A, I2 = - 12 A, I3 = 89 A.
Токи I1 и I2 получились отрицательными. Это означает, что направления их случайно были выбраны ошибочно. Ток I3 положителен; следовательно, его направление случайно выбрано правильно.
24

Ответ: I1 = - 85 A, I2 = - 12 A, I3 = 89 A.
Занятие № 19. Работа и мощность электрического тока. Закон Джоуля-Ленца Основные формулы:
1. Работа, совершаемая электростатическим полем и сторонними силами на участке цепи постоянного тока за время t:
A = IUt = I 2 Rt = U 2t
R
2.Закон Джоуля - Ленца:
1)в интегральной форме (применяется к элементу или участку цепи):
dA = dQ = I 2 Rdt = U 2 dt ; (14) R
t2
Q = ∫ I 2 (t)Rdt;
t1
2) в дифференциальной форме (применяется к малому объему пространства): ω = jE, где ω - удельная тепловая мощность;
3) Мощность тока: P = IU = I 2 R = U 2
R
3. Плотность тока: j = qn < v >
где n-концентрация носителей заряда; < v > - скорость направленного движения носителей (дрейфовая скорость); q - заряд носителей.
Примеры решения:
Пример № 1
По проводнику сопротивлением R=50 Ом течет ток, сила которого равномерно нарастает от Jo=1А до Jmax=4А за время t=6c. Определить за это время: 1) заряд, протекший по проводнику; 2) Выделившееся в проводнике количество теплоты.
Дано:
Jo = 1А Jmax = 4А t = 6с
R = 50 Ом Jmax = Jo+kt
q-?; Q-?
Решение:
По условию задачи сила тока равномерно растет, тогда закон изменения тока с течением времени имеет вид Jmax + kt,
где k коэффициент проводимости. Найдем k:
k = |
J max − J0 |
= |
(4 − 1) 1 |
A |
(1); |
||||
|
|
|
|
|
|
|
|||
t |
6 2 |
|
|||||||
|
|
c |
|
||||||
25
По определению: J = |
dq |
(2), тогда Dq = (J 0 + kt)dt (3); |
|
|
|
||
dt |
|
|
|
||||
|
|
|
|
|
|
||
|
|
q |
|
|
k t2 |
|
|
Проинтегрировав, получаем: ∫dq = ∫t (J0 + k t)dt (4); q = J0 |
t + |
(5); q=15 Kл. |
|||||
|
|||||||
|
|
0 |
0 |
2 |
|
||
Количество теплоты, выделившееся за бесконечно малый промежуток времени согласно закону
Джоуля-Ленца равно: dQ = J 2 Rdt = (J 0 + kt)2 Rdt = J0 |
2 Rdt + 2J0ktRdt + k 2t2 Rdt (6). |
||||
Проинтегрировав (6), и подставив численные значения k, R, Jo, t, получим: |
|||||
Q = J Rt + |
R t2 |
+ |
R t3 |
= 2100 Дж(7). |
|
2 |
12 |
|
|||
0 |
|
|
|
||
|
|
|
|
|
|
Ответ: q=15 Kл; Q=2100 Дж=2,1 кДж.
Пример № 2
Сколько ламп накаливания мощностью 150 Вт каждая, рассчитанных на напряжение 127 В, можно установить в помещении, если напряжение на зажимах генератора поддерживается равным 133 В. Проводка от генератора до потребителя выполнена алюминиевым проводом длинной 100м, с площадью поперечного сечения 14 мм2. Определить суммарную мощность тока потребителя.
Дано:
Ро=150Вт Uo=120B U=100B l =100м
S=15·10-6м2 ρ=2,9·10-8 Ом м
N-?; P-?
Решение:
Так как лампы соединены, то число ламп которые можно включить в данную цепь, найдем, разделив силу тока в магистральном проводе на силу тока Jo,
протекающего через одну лампу: N = J (1);
J0
Сопротивление подводящих проводов: R = |
ρ l |
(2); |
|
||||
S |
|
||||||
|
|
|
|
|
|
|
|
Сила тока в магистральном проводе: |
I = |
(U − U 0 ) |
|
(3), где |
(U - Uo)- |
||
|
R |
|
|
||||
|
|
|
|
|
|
|
|
падение напряжения в проводящих проводах.
Сила тока в 1 лампе: I = P0 (4);
U0
Число ламп: N = |
(U − U0 )U0 |
= |
(U − U0 )U0 S |
(5); |
R P0 |
|
|||
|
|
ρ l P0 |
||
Суммарная мощность тока потребителя: P = N P0 (U − U0 )U0 S (6);
ρ l
Расчет: N=26 ламп; Р=3,94 кВт Ответ: N=26 ламп; Р=3,94 кВт.
Пример № 3
26
В сеть с напряжением 220 В последовательно включили две лампы мощностью 60 Вт и 150 Вт, рассчитанные на напряжение U=110 В. Как распределятся напряжение на лампах? Какое количество теплоты выделится в каждой из ламп за 1 час работы? Каковы сопротивления ламп?
Дано: |
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Так как лампы соединены последовательно, то: |
|||||||||||||
U=220B |
||||||||||||||
U1=U2=110 B |
U = U1 + U 2 (1); R = R1 + R2 (2) , а текущей через каждую из ламп ток одинаков. |
|||||||||||||
Р1=60 Вт |
Сила тока в лампах: I = |
|
|
U |
|
|
(3); |
|
|
|
||||
Р2=150 Вт |
R1 + R2 |
|
|
|
||||||||||
t=3600c |
Мощность лампы: P = |
U1 |
2 |
|
|
(4); P |
= |
U 2 |
2 |
(5) |
||||
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
R1 |
|
|
|
|
|
2 |
|
R |
|
|
|
Q1 - ?; Q2 - ?; |
|
|
|
|
|
|
|
|
|
|
|
|||
P`1 − ? ; P`2 − ? ; |
Сопротивление ламп: R1 = |
U1 |
2 |
|
(6); R1 = 202 Oм; R2 = 81 Ом |
|||||||||
U`1 − ? ;U`2 − ? ; |
|
|
R1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
R1 - ?; R2 - ?; |
Зная R1 и R2 , рассчитаем силу тока в лампах согласно (3): I=0,78 A |
|||||||||||||
|
|
|||||||||||||
Рабочее напряжение на лампах вычислим по закону Ома для |
||||||||||||||
однородного участка цепи: U`1 = J R1 (8); U`2 |
= J R2 (9); U `1 = 157 B; U `2 = 63 B. Мощности, |
|||||||||||||
потребляемые лампами, равны, соответственно: |
P`1 = J U `= 122 Вт; P`2 = 49 Вт |
|||||||||||||
Количество теплоты, выделившееся на каждой из ламп, определится из закона Джоуля-Ленца:
Q = J 2 R t(10)? (т.е.)
Q1 = J 2 R1 t = 4 39 105 Дж; Q2 = 2,26 105 Дж.
Ответ: Q1 = 4,395 Дж; Q2 = 2,26 105 Дж; P’1 = 122 Вт; P’2 = 49 Вт; U’1 = 157 В; U’2 = 63 В; R1 = 202 Ом; R2 = 81 Ом; J = 0,78 A.
Пример № 4
Свинцовый предохранитель, включенный в сеть, плавится, если провод сети нагревается на 25оС. Провод сети сделан из алюминиевой проволоки площадью поперечного сечения 5 мм2: Найти площадь поперечного сечения проволоки свинцового предохранителя. Начальная температура свинцового предохранителя равна 293 К.
27

Дано:
S1 = 5 10−6 м2
p1 = 26 109 Ом м p2 = 2,7 10−7 Ом м
c1=880Дж/кг · К c2=120 Дж/кг · К d1=2,7 · 103кг/м3 d2=1,14 · 103кг/м3 T1=293К; T2=600К λ=2,5 · 104Дж/кг
T=25К
S2-?
Решение:
Введем обозначения: d1-плотность алюминия d2-плотность свинца
S1-площадь поперечного сечения алюминиевого проводника S2-площадь поперечного сечения свинцового проводника С1-удельная теплоемкость алюминия С2-удельная теплоемкость свинца
Количество теплоты, затраченной на нагревание алюминиевого провода рассчитаем по формуле: Q = С1 m T (1)
Масса m1 = d S1 11 (2)
Это количество теплоты полученное в следствие теплового действия
тока, тогда, с другой стороны: Q = |
t J |
2 ρ |
l |
(3) |
||
|
1 |
1 |
||||
|
1 |
|
|
S1 |
|
|
|
|
|
|
|
|
|
Приравняем (1) и (3): C1 m1 |
T = |
t J 2 |
ρ l |
(4) |
||
|
|
1 |
1 |
|||
|
|
|
S1 |
|
|
|
При протекании тока в свинцовом проводнике количество джоулей теплоты пошло на нагревание свинцового проводника и его расплав, т.е.
Q2 |
= |
J 2 |
ρ2 |
t |
= C2 |
d2 S2 (T1 |
+ T2 ) + S2 d2 λ (5) |
|
S2 |
|
|||||
|
|
|
|
|
|
|
Так как сила тока и время протекания тока одинаковы для алюминиевого и свинцового проводников, то можно исключить множители J и t:
Для этого поделим Q1 (3) на Q2 (5), и получим: |
Q1 |
= |
|
|
(C1 |
d1 S1 T ) |
(9) |
||
Q |
d |
2 |
S |
[C |
(T − T ) + λ ] |
||||
|
2 |
|
|
2 |
2 |
2 |
1 |
|
|
Из (6) получим формулу для расчета площади поперечного сечения свинцовой проволоки S2:
S2 = |
S1 |
|
C1 d1 ρ2 |
T |
|
(7) |
|
ρ1 d2 C2 |
|
|
|||
|
|
|
T λ |
|
||
Расчет: S2 = 4 10−6 м2
Ответ: S2 = 4 10−6 м2
Пример № 5
28
При поочередном подключении к источнику ЭДС двух электрических нагревателей с сопротивлением R1=3 Ом и R2=48 Ом в них выделяется одинаковая мощность Р=1,2 кВт. Определить силу тока Jкз при коротком замыкании источника.
Дано: |
Решение: |
|
|
|
|
|
|
|
Ε ; |
|
|
|
|
R1=3 Ом |
Ток короткого замыкания Jкз= |
|
|
|
||
R2=48 Ом |
|
|
r |
|
|
|
|
|
|
|
|
|
|
Р1=Р2=Р=1,2 кВт |
Внутреннее сопротивление источника определяется из источника |
|||||
|
равенства мощностей: Р = J 2 R = |
|
Ε R |
; P1=P2 |
||
|
|
(R + r)2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Jкз-? |
R1 |
R 2 |
R2 |
|
|
|
|
(R + r)2 = |
(R + r)2 → r = R1 |
(1) |
|
||
|
1 |
2 |
|
|
|
|
Величину Е можно определить из выражения для мощности при подключении любого из
нагревателей, например: Р = |
Е2 R |
→ E = P ( R1 + R2 ) (2), тогда |
|||||||
(R |
1 |
||||||||
+ r)2 |
|||||||||
|
|
|
|
|
|
|
1 |
|
|
Jкз = |
|
1 |
+ |
1 |
|
(3); |
|
|
|
Р |
R |
R |
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
|
|
1 |
|
2 |
|
|
|
|
|
Расчет: Jкз = 25А
Ответ: Jкз = 25А
Пример № 6
Поселок потребляющий электрическую мощность Р=1200 кВт, находится на расстоянии l=5 км от электростанции. Передача энергии производится при напряжении U=60 кВ. Допустимая относительная потеря напряжения (и мощности) в проводах k=1% Какой минимальный диаметр d могут иметь медные провода линий электропередачи?
Дано:
Р=1200 кВт l=5·103м U=6·104 B k=1%
d-?
Решение: Падение напряжения на проводах равно: k U (k=0,01), значит, напряжение на выходе линии электропередачи равно: (1-k) U . Из соотношения
P = (1− k ) U J получим силу тока в линии: J = |
|
|
|
Ρ |
|
≈ |
Ρ |
(1) |
||||
|
(1 − k) U |
U |
||||||||||
|
|
|
|
|
|
|
||||||
Значит сопротивление линии: R = |
kU |
2 |
(2) |
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
Считая линию двухпроводной, запишем: R = 2 |
ρ |
l |
= |
8 ρ l |
(3), |
|||||||
S |
π d 2 |
|||||||||||
|
|
|
|
|
|
|
|
|
||||
где ρ - удельное сопротивление меди;
Тогда: d = |
2 |
2 ρ l P |
(4) |
|
U |
π k |
|
29

Расчет: d=2.7 мм Ответ: d=2.7 мм
Пример № 7
Электропоезд метро идет по горизонтальному пути со скоростью V1, а затем со скоростью V2 преодолевает подъем с уклоном k=0,04. Потребляемая сила тока на горизонтальном участке J1=240А, а на подъеме J2=450А.Коэффициент сопротивления движению μ=0,02. Определить
соотношение скорости V1
V2
Дано: |
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
При равномерном движении по горизонтальному пути сила тяги: |
|||||||||||||||||
V1 |
|
|
||||||||||||||||||||
V2 |
|
|
F1 = μ m g , где m-масса электропоезда. |
|
|
|
|
|
|
|
|
|
||||||||||
k=0.02 |
|
|
При равномерном движении по наклонному участку: |
|
|
|||||||||||||||||
J1=240A |
|
|
F2 = m g(μ + k ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
J2=450A |
|
|
Соответственно развиваемая механическая мощность на горизонтальном участке: |
|||||||||||||||||||
|
|
|
|
|
||||||||||||||||||
μ=0,02 |
|
|
N1 = F1 V1 = μ m G V1 (1) , а на подъеме: N2 |
= F2 V2 |
= m g V2 (μ+ k )(2) |
|||||||||||||||||
|
|
|
|
|
Потребляемая электрическая мощность: |
|
|
|
|
|
|
|
|
|
||||||||
|
V1 |
-? |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V2 |
|
|
P1 = U J1 ; |
P2 = U J2 (3) где U- напряжение в сети. |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
N |
1 |
|
N |
2 |
|
V |
|
J |
1 |
|
|
k |
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Считая, что КПД двигателя неизменно, то: |
|
= |
|
;→ |
|
1 |
= |
|
1 |
+ |
|
(4) |
||||||||||
|
|
P |
|
V |
|
J |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
P |
|
|
2 |
|
2 |
|
|
μ |
||||||
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
||||
Расчет: |
V1 |
=1,6; Ответ: |
V1 |
=1,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
V2 |
V2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример № 8
Источник тока с ЭДС Е и внутренним сопротивлением r замкнут на реостат. Построить графики зависимости от сопротивления следующих величин:
силы тока J; напряжения U; мощности Р во внешней цепи; полной мощности Ро и КПД цепи η. При каком сопротивлении достигается максимальная мощность во внешней цепи. Каков при этом КПД цепи?
30
