2. Построение математической модели двигателя постоянного тока и системы тестирования

2.1 Математическая модель дпт

Важное свойство ДПТ с независимым возбуждением от постоянных магнитов состоит в том, что результирующий момент сил от всех проводников якоря, называемый электромагнитным моментом двигателя M, пропорционален току якоряI_я, потребляемому двигателем от источника питания вычисляется по формуле 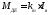2.1:

(2.1)

где k_m - коэффициент пропорциональности, называемый постоянной момента двигателя. Его размерность [Нм/А].

По законам электромагнитной индукции в проводнике, движущемся в магнитном поле, возникает электродвижущая сила. Суммарная ЭДС катушек якоря E через коллектор и щетки прикладывается к внешним выводам двигателя. В двигательном режиме работы эта ЭДС направлена против внешнего напряжения Uя, подведенного к якорю от источника питания. Поэтому ЭДС двигателя часто называется противоЭДС. Она прямо пропорциональна угловой скорости вращения вала двигателя ω_дв[рад/с] (формула 2.2):

(2.2)

где k_ω - коэффициент пропорциональности, называемый постоянной ЭДС двигателя. Его размерность [Вс/рад].

Природа электромагнитных явлений в ДПТ такова, что если используется система единиц СИ, то значения коэффициентов kω и km численно равны.

Рассмотрим уравнения, описывающие электрические процессы в ДПТ. В электрической якорной цепи двигателя протекает ток I_я под действием напряжения постоянного тока U_a  источника питания и противоЭДС двигателя [15].

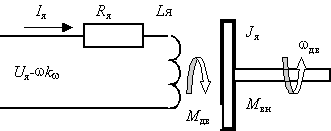
Рисунок 2.1 - Якорная цепь двигателя

Эта цепь характеризуется параметрами: активным сопротивлением Rя [Ом] и индуктивностью L_я[Гн] якорной обмотки. Вращающийся ротор, обладающий моментом инерции J_a[Нмс²/рад], приводится в движение одновременным действием электромагнитного момента двигателя M_дв и момента внешних сил M_вн, приложенного к валу двигателя.

Исходные дифференциальные уравнения ДПТ составляются на основании законов физики. Для электрической цепи используется второй закон Кирхгофа, согласно которому можно записать уравнение

(2.3)

где член R_яI_я характеризует падение напряжения на активном сопротивлении якорной цепи в соответствии с законом Ома, а членL_я(dI_я/dt) отражает наличие ЭДС самоиндукции, возникающей в обмотке при изменении тока якоря. В уравнении 2.3 не учитывается падение напряжения на щетках, зависящее нелинейно от тока якоря, но имеющее, как правило, относительно небольшое значение по сравнению с напряжениемU_я.

Дифференциальное уравнение, характеризующее процессы в механической части двигателя, составляется на основании второго закона Ньютона:

(2.4)

где M_вн - момент внешних сил, действующий относительно оси вращения вала двигателя. В уравнении 2.4 не учитывается действие сил трения, возникающих при вращении ротора, но оказывающих относительно слабое действие на ускорение вала ДПТ.

Используя вышеприведенные формулы и приводя дифференциальные уравнения к нормальной форме Коши, получим описание ДПТ в форме:

(2.5)

Для исследования процессов с помощью ЭВМ удобно использовать структурное представление математической модели ДПТ. Для этого преобразуем систему линейных дифференциальных уравнений 2.5 по Лапласу при нулевых начальных условиях. В результате получим систему алгебраических уравнений:

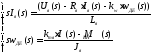(2.6)

в которых s - переменная Лапласа, а величины I_я(s), w_дв(s), U_я(s), M_вн(s) - изображения по Лапласу переменных I_я, w_дв, U_я, M_вн соответственно. После эквивалентных преобразований системы 2.6 эти уравнения могут быть представлены в форме:

(2.7)

где Т_э = L_я/R_я - электромагнитная постоянная времени якорной цепи двигателя.

По уравнениям 2.7 может быть сформирована структурная схема ДПТ для его математического моделирования (рисунок 2.2) [15].

Важным параметром ДПТ, определяющим его динамические свойства, является электромеханическая постоянная времени двигателя, вычисляющаяся по формуле 2.9:

(2.9)

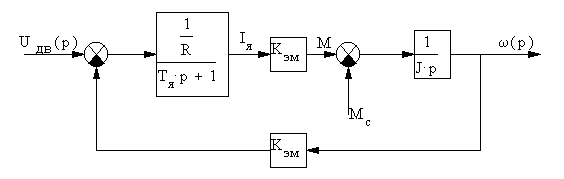
Рисунок 2.2–Структурная схема ДПТ

Зависимость между электромагнитным моментом двигателя и частотой вращения ротора в установившемся режиме при постоянных Uя и Mвн называется механической характеристикой двигателя. Уравнение механической характеристики имеет вид:

(2.10)

При пуске двигателя, когда скорость равна нулю, развивается пусковой момент, определяющийся по формуле 2.11:

(2.11)

Частота вращения вала двигателя при отсутствии сопротивления называется частотой вращения холостого хода, которая находится по формуле 2.12 [15]:

(2.12)