
diagnostika-podshipnikov-kacheniya-s-pomoschyu-nepreryvnogo-veyvlet-preobrazovaniya
.pdf
Акутин М.В., Ваньков Ю.В., Кондратьев А.Е.
ДИАГНОСТИКА ПОДШИПНИКОВ КАЧЕНИЯ С ПОМОЩЬЮ НЕПРЕРЫВНОГО ВЕЙВЛЕТ ПРЕОБРАЗОВАНИЯ
Для повышения достоверности результатов вибродиагностики подшипников качения рассмотрено применение непрерывного вейвлет-преобразования полезного сигнала. Сравнение скейлограмм дефектных и бездефектных подшипников осуществлено с помощью PSNR метрики, построение алгоритма записи полезного сигнала произведено в программной среде LabView.
Актуальность проблемы виброакустической диагностики диктуется острой необходимостью организации оперативного безразборного контроля технического состояния машин и механизмов на всех стадиях их жизненного цикла. Подшипник качения является наиболее распространенным элементом конструкции любого роторного механизма и, в то же время, наиболее уязвимым элементом. Подшипники осуществляют пространственную фиксацию вращающихся роторов и именно подшипники воспринимают большую часть статических и динамических усилий, возникающих в работающем механизме, поэтому состояние подшипников является важнейшим показателем исправности и работоспособности механизма.
Практические задачи диагностики подшипников качения в процессе эксплуатации решаются, как правило, одним из трех основных способов. Первый использует алгоритмы обнаружения дефектов по росту температуры подшипникового узла, второй - по появлению в смазке продуктов износа, а третий - по изменению свойств вибрации (шума). Наиболее полная и детальная диагностика подшипников с обнаружением и идентификацией дефектов на ранней стадии развития выполняется по сигналу вибрации подшипника.
В подшипниках качения встречаются различные типы дефектов. К основным дефектам относятся: усталостные разрушения, выкрашивание, абразивный износ, атмосферная коррозия, фреттинг, бриннелирование, электроповреждения, натиры, задиры. При перегреве обычно происходит полный отказ подшипника, а повреждение сепаратора проявляется в образовании в нем трещин с последующим разрушением.
Важной проблемой идеи виброакустической диагностики является получение устойчивого сигнала для последующей обработки. С этой целью в КГЭУ разработан и изготовлен стенд для виброакустической диагностики подшипников и на базе LabView 7.1 программное обеспечение «DetectFault» (свидетельство о государственной регистрации программы для ЭВМ №2008610104).
Среда разработки лабораторных виртуальных приборов LabView (Laboratory Virtual Instrument Engineering Workbench) представляет собой среду прикладного графического программирования, используемую в качестве стандартного инструмента для проведения измерений, анализа их данных и последующего управления приборами и исследуемыми объектами [1]. LabView может использоваться на компьютерах с операционными системами Windows, MacOS, Linux, Solaris и HP-UX. LabView позволяет разрабатывать практически любые приложения, взаимодействующие с любыми видами аппаратных средств, поддерживаемых операционной системой компьютера. В основе технологии использования LabView лежит комбинированное моделирование систем на ЭВМ, состоящее из аналитического, имитационного и натурного. Несомненные преимущества LabView — простота при разработке программ, называемых виртуальными приборами (ВП) и широкий набор функциональных возможностей языка и среды программирования.
Программа «DetectFault» включает в себя следующие основные части: программу регистрации акустических сигналов; программу формирования эталонных спектров; программу сравнения спектров с эталоном.
Все эти составные части объединены в одной интегрированной оболочке.
Формирование эталонного спектра - это процесс почастотного перехода от совокупности амплитуд исходных спектров на данной частоте (а1, а2, а3, ..., аn) к единственному (обобщенному, эталонному) значению аs. Предполагается, что эталон будет содержать только общие, характерные для всей совокупности спектров, данные и не должен содержать какие-либо (случайные) особенности отдельного спектра.
Эталонный спектр формируется медианным усреднением
as
med a |
|
|
i |
i |
|
|
|
|
.
Сравнение с эталоном анализируемых спектров сводится к регистрации отличий этих спектров от эталона по группе параметров к которым относят: коэффициент корреляции, непараметрическая ранговая оценка Спирмена, статистика знаков (Фишера), ранговая сумма Уилкоксона [2].
Для вычисления выборочного коэффициента корреляции r используется зависимость: |
|||||||
r |
|
ai as i |
ai as i n |
|
|
, |
|
ai |
ai |
|
n as i as i |
2 |
n |
||
|
2 |
|
|||||
|
2 |
|
|
2 |
|
|
|
упрощающая вычисления (при этом суммирование выполняется для значений индекса i, изменяющихся в диапазоне от 1 до n ).
В дополнение к изложенной выше стандартной оценке коррелированности проверяемого и эталонного спектров вычисляется и непараметрическая ранговая оценка Спирмена:
|
|
6 |
|
n |
|
|
r 1 |
|
|
rank ai rank asi 2 , |
|
||
|
|
|
|
|||
|
n (n2 1) i 1 |
|
|
|||
где rank |
ai |
— ранг амплитуды |
ai |
в вариационном ряду амплитуд проверяемого спектра (т.е. номер ме- |
||
ста, которое |
эта амплитуда занимает среди всех амплитуд данного спектра, упорядоченных по возраста- |
|
нию); rank |
a |
si — то же для эталонного спектра. |
|
||
Статистика знаков (Фишера) S вычисляется как количество частот положительной амплитуды разностного спектра (к этой сумме добавляется половина количества частот нулевой амплитуды).
Ранговая сумма Уилкоксона вычисляется по следующему алгоритму:
смесь амплитуд
ai
и |
a |
|
si
(индекс i изменяется от 1 до n) упорядочивается по возрастанию;
суммируются ранги амплитуд ai в полученном вариационном ряду — это и есть ранговая сумма Уилкок-
сона W (при каждом совпадении значений амплитуд ai и asi к этой сумме прибавляется полусумма рангов
этих амплитуд); Для классификации объектов «годный» или «дефектный» по всем выбранным параметрам доверительные
интервалы объединяет подход, характерный для процедур отбраковки аномалий: программа анализа интерпретирует совокупность вычисленных значений некоторой статистики (p1, p2, …, pm) как множество измеренных значений некоторого абстрактного параметра и применяет к этой совокупности значений следующую процедуру:
вычисляется оценка положения p ;

вычисляется оценка разброса S как MAD относительно оценки положения; для заданного уровня значимости строится доверительный интервал
p S t(1 |
|
|
2 |
||
|
,
m
2)
,
где t( , m) — -квантиль распределения Стьюдента с m степенями свободы.
Экспериментальные исследования показали что для повышения чувствительности виброакустического метода необходимо променять альтернативные методы обработки и анализа сигналов одним из таких методов является вейвлет - анализ [3].
Вейвлет - анализ представляет собой особый тип линейного преобразования сигналов и отображаемых этими сигналами физических данных о процессах и физических свойствах объектов. Базис собственных функций, по которому проводится разложение сигналов, обладает многими специальными свойствами и возможностями. Они позволяют сконцентрировать внимание на тех или иных особенностях анализируемых процессов, которые не могут быть выявлены с помощью традиционных преобразований Фурье и Лапласа.
Реальные сигналы, как правило, конечны и принадлежат пространству L2(R). Частотный спектр сигналов обратно пропорционален их длительности. Соответственно, достаточно точный низкочастотный анализ сигналов должен производиться на больших интервалах, а высокочастотный – на малых. Если частотный состав сигнала претерпевает существенные изменения на интервале его задания, то преобразование Фурье дает только усредненные данные частотного состава сигнала с усредненным частотным разрешением. Определенная частотно-временная локализация анализа создается применением оконного преобразования Фурье, при котором сигнал просматривается в пределах оконной функции с последовательными сдвигами во времени, что дает семейства частотных спектров, локализованных во времени в пределах постоянной ширины окна оконной функции, а, следовательно, с постоянным значением частотного разрешения.
В отличие от оконного преобразования Фурье, вейвлет -преобразование, при аналогичных дискретных значениях сдвигов b, дает семейства спектров масштабных коэффициентов а сжатия-растяжения
с(a,b) =
s(t) |а|-1/2ψо[(t-b)/а]dt.
где, s(t) сигнал, ψо вейвлет.
Если считать, что каждый вейвлет имеет определенную "ширину" своего временного окна, которому соответствует определенная "средняя" частота Фурье-образа вейвлета, обратная его масштабному коэффициенту а, то семейства масштабных коэффициентов вейвлет-преобразования можно считать аналогичными семействам частотных спектров оконного преобразования Фурье, но с одним принципиальным отличием. Масштабные коэффициенты действуют во времени, изменяя "ширину" вейвлетов и, соответственно, "среднюю" частоту их Фурье -образов, а, следовательно, каждой частоте соответствует своя длительность временного окна анализа, и наоборот. Многоразмерное временное окно вейвлет -преобразования позволяет одинаково хорошо выявлять и низкочастотные, и высокочастотные характеристики сигналов.
Достоинства и недостатки вейвлетных преобразований:
вейвлетные преобразования обладают практически всеми достоинствами преобразований Фурье; вейвлетные базисы могут быть хорошо локализованными как по частоте, так и по времени. При выделе-
нии в сигналах хорошо локализованных разномасштабных процессов можно рассматривать только те масштабные уровни разложения, которые представляют целевой интерес;
вейвлетные базисы, в отличие от преобразования Фурье, имеют достаточно много разнообразных базовых функций, свойства которых ориентированы на решение различных задач. Базисные вейвлеты могут иметь и конечные, и бесконечные носители, реализуемые функциями различной гладкости;
Недостатком вейвлетных преобразований является их относительная сложность реализации.
Базисными функциями вейвлетов могут быть самые различные функции - модулированные импульсами синусоиды, функции со скачками уровня и т.п., что и обеспечивает хорошее представление сигналов с локальными особенностями, в том числе со скачками, разрывами и перепадами значений с большой крутизной, при подборе соответствующего типа вейвлетов. При анализе произвольных сигналов использование разнотипных вейвлетов позволяет повысить достоверность выделения локальных особенностей сигналов.
Результатом вейвлет -преобразования одномерного числового ряда (сигнала) является двумерный массив амплитуд – значений коэффициентов С(a,b). Распределение этих значений в пространстве (a,b) = (временной масштаб, временная локализация) дает информацию об изменении относительного вклада вейвлетных компонент разного масштаба во времени и называется спектром коэффициентов вейвлет - преобразования, масштабно-временным (частотно-временным) спектром , вейвлет -спектром (wavelet spectrum) и скейлограммой.
Спектр C(a,b) одномерного сигнала представляет собой поверхность в трехмерном пространстве. Способы визуализации спектра могут быть самыми различными.
Сравнение скейлограмм, полученных непрерывным вейвлет преобразованием, проводилось при помощи PSNR-метрики. Пиковое отношение сигнала к шуму обозначается аббревиатурой PSNR (peak signal-to-noise ratio) и является инженерным термином, означающим соотношение между максимумом возможного значения сигнала и мощностью шума, искажающего значения сигнала. От исследуемых сигналов формируются скейлограммы, полученные непрерывным вейвлет преобразованием и сравниваются с эталонной скейлограммой.
Эталонная скейлограмма |
формируется |
медианным усреднением скейлограмм бездефектных подшипников |
||||||||||||||
Cs (a,b) med C(a,b) |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
i |
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
PSNR 20 Log |
|
|
|
Max_value |
|
|
|
|
|
, где |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
s |
|
f2 |
|
|
|
|
|
|
|||||||
|
|
|
min(b |
,b) |
s |
|
|
j |
2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Сi j Ci |
|
|
|
|
|
||||||||
|
|
|
i 0 |
|
j f1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
min(b |
s |
,b) |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Max_value – амплитуда сигнала максимально возможной мощности, допустимая в данном представлении
звукового |
сигнала; Сis j и |
Сi j значения амплитуд скейлограмм эталонного и исследуемого подшипни- |
||
ка, bs и |
b количество сдвигов вейвлет базиса для первого и второго сигнала соответственно; f |
и f |
2 |
|
|
|
1 |
|
|
– параметры, отфильтровывающие из общей скейлограммы частотную полосу для исследования.
Преимущество данного метода заключается в том, что он не чувствителен к фазе сигнала, а также в том, что появляется возможность рассмотрения искажений в отдельных частотных диапазонах.
Для классификации объектов «годный» или «дефектный» по PSNR-метрики применялась та же процедура, что и для сравнения сигналов по спектрам, приведенная выше.
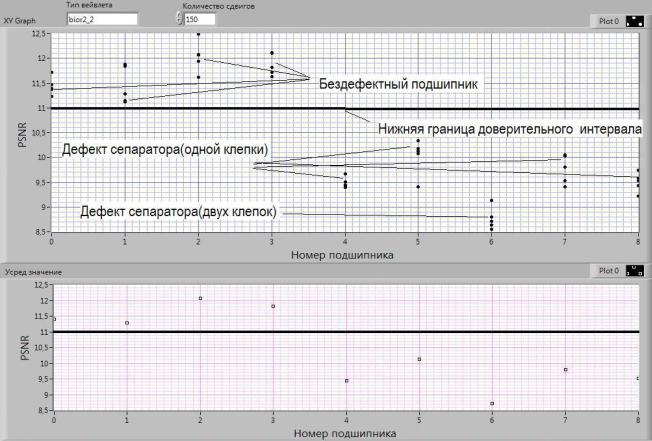
Выбор типа вейвлет базиса проводился в следующей последовательности: находилось значение PSNR метрики для нескольких замеров с одного подшипника, вычислялась оценка разброса данных значений и выбирался тип вейвлета базиса, где это значение минимально. По результатам анализа определено, что наиболее подходящими являются: ортогональные вейвлеты с компактным носителем (вейвлеты Добеши dbN и Койфлета coifN) и биортогональные вейвлеты с компактным носителем (biorNr . Nd и rbioNr . Nd) [4]. Пример применения PSNR метрики для определения дефектов подшипника (подшипники VDYD 6208, частота вращения 1820 об/мин) показан на рис.1.
Рис. 1. Пример сравнения PSNR метрик с помощью вейвлета bior2_2
Применение вейвлет анализа и сравнение скейлограмм PSNR метрикой, полученных при помощи непрерывного вейвлет преобразования обеспечивают хорошую сходимость результатов экспериментов и устойчивое определение дефектов разного рода.
ЛИТЕРАТУРА
1.Суранов А.Я. LabView 7: Справочник по функциям. – М.: ДМК Пресс, 2005. – 512с.
2.Вардер Б.Л. Математическая статистика. – М.: ИИЛ, 1960. – 436 с.
3.Новиков Л.В. Основы вейвлет-анализа сигналов. Учебное пособие. 1999. 152 с.
4.Adhemar Bultheel. Wawelets with application in signal and image processing. 2002. – 181 c.
