
- •Министерство транспорта и связи Украины Государственная администрация связи Одесская национальная академия связи им. А. С. Попова Кафедра сетей связи
- •Содержание
- •Построение моделей телекоммуникационной сети
- •Синтез сети абонентского доступа
- •Синтез сети межузловой связи
- •Нахождение кратчайших путей
- •Построение маршрутных матриц
- •Оценка пропускной способности сети между парой пунктов
- •Список литературы и программного обеспечения
Министерство транспорта и связи Украины Государственная администрация связи Одесская национальная академия связи им. А. С. Попова Кафедра сетей связи
КОМПЛЕКСНОЕ ЗАДАНИЕ
на тему:
ЭЛЕМЕНТЫ СИНТЕЗА И АНАЛИЗА ТЕЛЕКОММУНИКАЦИОННЫХ СЕТЕЙ
Студента 3-го курса группы
|
Студент |
|
|
|
Руководитель |
|
|
|
Проверила |
|
|
Одесса – 2011
Содержание
Исходные данные 3
Построение моделей телекоммуникационной сети 4
Синтез сети абонентского доступа 8
Синтез сети межузловой связи 10
Нахождение кратчайших путей 14
Построение маршрутных матриц 20
Оценка пропускной способности сети между парой пунктов 31
Вывод 33
Список литературы и программного обеспечения 34
Исходные данные Таблица 1.1 – Исходные данные
Из
1
1
1
1
1
2
2
3
3
4
5
5
6
6
6
7
8
8
9
В
2
4
5
7
8
3
4
6
7
6
6
8
7
8
9
10
9
10
10
Вес
50
12
30
55
75
10
15
90
99
10
70
80
19
73
40
10
33
7
3
Источник: 2.
Сток: 4.
Построение моделей телекоммуникационной сети
Задача синтеза носит технико-экономических характер — задачи выбора отпимальной топологии сети, оптимального колличества и места расположе- ния узлов коммутации.
Задача анализа — задача нахождения оптимальных путей передачи ин- формационных сообщений, определения совокупности путей заданной тран- зитности, оценки пропскной способности сети, вероятности установления со- единения между пунктами.
Модельное представление позволяет выявить и отразить наиболее суще- ственные, с точки зрения стоящей проблемы, элементы объекта и связи меж- ду ними, не отвлекаясь на детали.
Существует несколько форм модельного представления. Граф — некоторая совокупность вершин и ребер (дуг).
Граф, в котором задано направление дуг, называется ориентированным, в противном случае — неориентированным.
Между двумя вершинами, соединенными дугой (ребром) существует от- ношение смежности (для ориентированного графа вершины i и j смежны лишь если дуга начинается в i и заканчивается в j.
Между вершиной и соединенными с ней дугами (ребрами) существует от- ношение инцидентности.
Матрица смежности — это матрица A = [[aij ]] размером (n× n), элементы
которой могут принимать следующие значения:
aij = 1, если в графе существует ребро (дуга) между i и j,
aij = 0, если ребра (дуги) между i и j в графе не существует.
Сетевая модель — это взвешенный граф, веса которого обозначают по- пускную способность или длины линий.
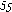
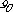

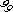
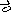
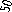
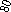
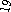


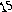
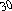
Рисунок
2.1
–
Граф
заданной
сети



Таблица 2.1 – Матрица смежности
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
|
2 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
3 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
4 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
5 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
|
6 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
|
7 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
8 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
9 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
|
10 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
Таблица 2.2 – Матрица инцидентности
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
(1; 2) |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
(1; 4) |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
(1; 5) |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
|
(1; 7) |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
(1; 8) |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
|
(2; 3) |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
(2; 4) |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
(3; 6) |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
(3; 7) |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
(4; 6) |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
|
(5; 6) |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
|
(5; 8) |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
|
(6; 7) |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
(6; 8) |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
|
(6; 9) |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
(7; 0101010) |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
|
(8; 9) |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
|
(8; 10) |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
|
(9; 10) |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
Таблица 2.3 – Матрица весов
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
0 |
50 |
0 |
12 |
30 |
0 |
55 |
75 |
0 |
0 |
|
2 |
50 |
0 |
10 |
15 |
0 |
0 |
0 |
0 |
0 |
0 |
|
3 |
0 |
10 |
0 |
0 |
0 |
90 |
99 |
0 |
0 |
0 |
|
4 |
12 |
15 |
0 |
0 |
0 |
10 |
0 |
0 |
0 |
0 |
|
5 |
30 |
0 |
0 |
0 |
0 |
70 |
0 |
80 |
0 |
0 |
|
6 |
0 |
0 |
90 |
10 |
70 |
0 |
19 |
73 |
40 |
0 |
|
7 |
55 |
0 |
99 |
0 |
0 |
19 |
0 |
0 |
0 |
10 |
|
8 |
75 |
0 |
0 |
0 |
80 |
73 |
0 |
0 |
33 |
7 |
|
9 |
0 |
0 |
0 |
0 |
0 |
40 |
0 |
33 |
0 |
3 |
|
10 |
0 |
0 |
0 |
0 |
0 |
0 |
10 |
7 |
3 |
0 |
Таблица 2.4 – Структура смежности
|
|
Смежные вершины |
|
1: |
2,4,5,7,8 |
|
2: |
1,3,4 |
|
3: |
2,6,7 |
|
4: |
1,2,6 |
|
5: |
1,6,8 |
|
6: |
3,4,5,7,8,9 |
|
7: |
1,3,6,10 |
|
8: |
1,5,6,9,10 |
|
9: |
6,8,10 |
|
10: |
7,8,9 |
В виде массива
. .
R = . .
.
.
|
1, 1, 1, 1, 1, |
2, 2, |
3, 3, 4, 5, |
5, 6, 6, 6, 7, 8, 8, 9 |
|
2, 4, 5, 7, 8, |
3, 4, |
6, 7, 6, 6, |
8, 7, 8, 9, 10, 9, 10, 10 |
. .
. .
