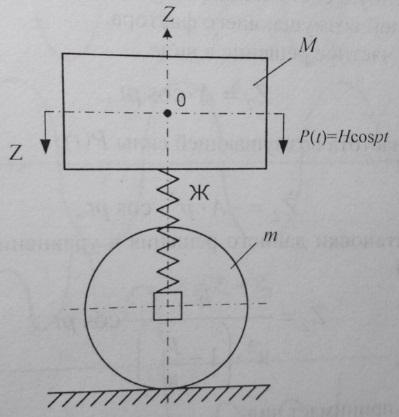
6 Свободные вертикальные колебания экипажа с одноярусным рессорным подвешиванием

М – масса подрессоренных частей экипажа, Z – текущая координата вертикальных перемещений центра тяжести подрессоренных частей, Ж – жесткость упругого рессорного подвешивания (кН/м), m – масса неподрессоренных частей экипажа.

Пусть под воздействием единичного возмущения подрессоренная масса получит некоторую динамическую переменную Z₁, что вызовет появление 2-х вертикальных сил: силы инерции (M*Z₁) и упругие силы (Ж*Z₁)

Под действием упругих сил система будет стремиться в исходное состояние.

Под действием сил инерции подрессоренная масса будет проскакивать положение равновесия, совершая периодические колебательные движения.

Уравнение динамического равновесия системы: или , где – круговая частота, 1/с.

1. Свободные колебания подрессоренной массы М носят синусоидальный характер с круговой частотой К. Эти колебания являются незатухающими, если в системе отсутствуют силы сопротивления (гасители колебаний).

2. Частота свободных незатухающих колебаний величина постоянная, зависящая только от инерционных и упругих переменных системы и не зависят от других условий.

3. Амплитуда свободных колебаний определяется параметрами системы и начальными условиями.

7 Вынужденные вертикальные колебания экипажа с одноярусным рессорным подвешиванием

Колебания происходят в результате действия периодически повторяющейся во времени силы P(t)/

Уравнения колебаний

Полное решение уравнения такого вида будет состоять из суммы общего решения однородного уравнения Z₁ и частного Z₂.

Частное решение Z₂ характеризует вынужденную составляющую колебаний

, где p – круговая частота возмущающей силы P(t).

, где Z₁ – свободные колебания, а Z₂ – вынужденные.

Под действием внешней периодически повторяющейся силы Р надрессорное строение совершает сложные колебательные движения, являющиеся результатом действия друг на друга свободных и вынуждающих колебани. При этом свободные колебания имеют частоту k=const, частота вынужденных колебаний определяется частотой возмущающей силы p≠const.

8 Резонанс колебаний

При рассмотрении колебаний наибольший интерес представляют вынужд. колеб; амплитуда которых (Z₂) изменяется вместе с частотой внешних сил. , при р=k

Амплитуда увеличивается в течение каждого периода колебания на величину ΔZp. Этот процесс нарастания амплитуды называется резонансом колебаний. Если не будут приняты меры к ограничению амплит. колебан. в режиме резонанса могут создаться неблагоприятные условия для работы , вплоть до ее разрушения. Колебания, происходящие с одной из частот свободн. колебан. могут привезти к аварийной ситуации. Эти колебания называются главными колебаниями, а частоты свободных колебаний рассматриваемой сис-мы называются главными частотами.

9 Свободные вертикальные колебания систем с двумя степенями свободы

Z1, Z2 – координаты вертикальных перемещений центров тяжести масс кузова и подресс. частей тележки.

Уравнение колебаний кузова:

– уравн. колебан. подрессорен. части.

K1,K2,K3-состовляющие порциальные частоты вертикальных колеб.

Решения уравнений:

– частоты сложного процесса свободных колебаний

Как и в экипаже с 1-ярусным подвешиванием. частоты свобод. чолеб. зависят только от инерции и упругих параметров сис-мы. В процессе колебаний подресор. массы совершают вертикальные перемещения с амплитудой А и В одновременно, т.е. происходит наложение колебаний друг на друга.