16)Геометрический смысл опр.Интеграла

Пусть на отрезке задана непрерывная неотрицательная функция . Криволинейной трапецией называется фигура, ограниченная сверху графиком функции y = f(x), снизу - осью Ох, слева и справа - прямыми x = a и x = b

Определенный интеграл от неотрицательной функции с геометрической точки зрения численно равен площади криволинейной трапеции, ограниченной сверху графиком функции , слева и справа - отрезками прямых и , снизу - отрезком оси Ох.

17) Формула Ньютона — Лейбница или основная теорема анализа даёт соотношение между двумя операциями: взятием определённого интеграла и вычислением первообразной.

Если функция F(x) – какая-нибудь первообразная от непрерывной на отрезке [a,b] функции f(x), то(1)

Доказательство. В силу того, что f(x) непрерывна на [a,b], она имеет первообразную F(x) во всех точках промежутка. Так как две первообразные отличаются на постоянное слагаемое, то существует C, такое, что

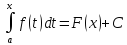(2)

Равенство верно при x принадлеж. [a,b]. Подставим в (2) два значения:

X=a и x=b. При x=a получим иF(a)+C=0, т.е. С=-F(a),

При x=b , что и требовалось доказать.

Тогда формула Ньютона-Лейбница

18)Замена переменной в определенном интеграле

Пусть дан интеграл , гдеf(x)-непрерывная на отрезке [a,b] функция. Введем новую переменную x=φ (t). Если φ (α)=a, φ (β)=b, значения φ (t) не выходят за пределы [a,b], когда t изменяется в [α,β]. Если φ (t), φ ’(t) непрерывны на отрезке [a,b], тогда f[φ (t)] φ ’(t) непрерывна на отрезке [α, β] и =φ ’(t)dt.

В отличие от неопределенного интеграла замена переменных в определенном интеграле предполагает изменение не только подынтегрального выражения, но и пределов интегрирования.

19)Интегрирование по частям в определенном интеграле

Пусть функции υ=υ(x), ν=v(x) дифференцируемы в [a,b]. Тогда .

Доказательство: 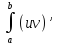dx=.

Отсюда легко получается нужное равенство.

Пример: . Обозначимx=u, sinxdx=dv. Отсюда получим du=dx, v=-cosx,

+ =π.

20)Геометрическое приложение определенного интеграла

  Если на отрезке     функция, то площадь криволинейной трапеции, ограниченной кривой, осьюи прямыми(рис. 9), равна

Если     на отрезке, то площадь соответствующей криволинейной трапеции

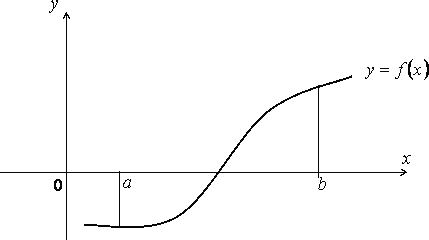
В общем случае, когда функция     меняет знак на отрезке(рис. 10), площадь, ограниченная кривой, осьюи прямымиможет быть найдена как сумма площадей фигур, лежащих выше и ниже оси. Иначе

21,22,23 . Несобственный интеграл; первого и второго порядков.

Пусть функция определена для всех, где- некоторое число, и интегрируема на любом отрезке, где. Если существует конечный предел

Тогда, если существует конечный предел . ,то его называют несобственным интегралом первого рода отf(x) в промежутке [a;∞) и обозначают

(1)

Если этот предел существует и конечен, то говорят, что несобственный интеграл (1) сходится. Если не существует - расходится.

Формула Ньютона-Лейбница:

Геометрический смысл.

Это площадь криволинейной трапеции, заключенной между y=f(x)x=aи осью абсцисс.

Несобств. инт второго рода-несобств интеграл от разрывных фунуций.

24. Диф уравнение. Задача Коши

Д.У. наз уравнение, связывающее независимую переменную х, ф-циюy=y(x) и её производные или дифференциалы.

 F(x₁,x₂,x₃,..,y,y′,y′′,...y⁽ⁿ⁾) = 0

Если ур-е имеет одну независимую переменную, то оно наз обыкновенным Д.У., если же 2 или более переменных, то ур-е наз. Д.У. в частных производных.

Порядком Д.У. наз наивысший порядок производной в него входящей.

Общим решениемд.у. наз такая дифференцируемая ф-ция у=у(х,С), кот при подстановке обращает его в тождество

Задачей Кошиназ. Нахождение любого частного решения д.у. вида у=у(х,С₀), удовлетворяющего начальным условиям y(x₀)=y₀