1)Определение функции двух переменных

Если каждой паре ( x;y) значений двух независимых друг от друга переменных величин х и у из некоторого множества D соответствует единственное значение величины, то говорят, что z есть функция двух независимых переменных x и y, определенная на множестве D.

Обозначается: z=f(x;y) или z=z(x;y).

Например, S=ab, S=S(a;b)- функции двух переменных; V=abc, V=V(a,b.c) – функция трех переменных;

2)Область определения ф-ии двух переменных

Область определения функции z=f(x,y) называется совокупность пар чисел (x,y), которым соответствуют действительные значения функции. D={(x,y)}

Множество Z={f(x,y)} – множество значений функции.

3)График функции двух переменных. Линии уровня. Поверхности уровня.

Графиком функции z= f(x,y) называется поверхность, представляющая собой геометрическое место точек функции, когда точка (x,y) принимает все значения из области определения.

Линией уровня функции z= f(x,y) называется геометрическое место точек (x,y) плоскости, в которой функция принимает одно и то же значение С. Линию уровня можно построить, спроектировав на плоскость XOY множество точек пространства. Уравнение линии уровня имеет вид f(x,y)=С.

Поверхностью уровня u=с функции u= f(x,y,z) называется поверхность f(x,y,z)=с, в точках которой функция u= f(x,y,z) сохраняет значение, равное с.

4)Предел и непрерывность ф-ии нескольких переменных.

Введем понятие D-окрестности точки М0 (Х0 , у0) на плоскости ОХу как круга радиуса D с центром в данной точке. Аналогично можно определить D-окрестность в трехмерном пространстве как шар радиуса D с центром в точке М0 (Х0 , у0 , Z0). Для N-мерного пространства будем называть D-окрестностью точки М0 множество точек М С координатами , удовлетворяющими условию

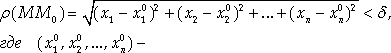
Координаты точки М0. Иногда это множество называют «шаром» в N-мерном пространстве.

Число А называется Пределом функции нескольких переменных

В точке М0, если

Такое, что | F(M) – A| < ε для любой точки М из δ-окрестности М0.

Обозначения:

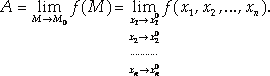
Необходимо учитывать, что при этом точка М может приближаться к М0, условно говоря, по любой траектории внутри D-окрестности точки М0. Поэтому следует отличать предел функции нескольких переменных в общем смысле от так называемых Повторных пределов, получаемых последовательными предельными переходами по каждому аргу

Функция Называется Непрерывной в точке М0 Если

Если ввести обозначения

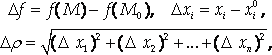
То это условие можно переписать в форме

Внутренняя точка М0 Области определения функции Z = F (M) называется Точкой разрыва функции, если в этой точке не выполняется условие

Замечание. Множество точек разрыва может образовывать на плоскости или в пространстве Линии Или Поверхности разрыва.

5)Определение частных производных

Частные производные функции y=f(M)в том случае, если они существуют не в одной точке, а на некотором множестве A’, являются функциями, определенными на этом множестве. Поэтому удобно ввести следующие обозначения:

F’x1=g1(M), f’x2=g2(M)….

Полученные функции g1, g2….gn, определенные в A’, могут быть непрерывными и иметь частные производные в различных точках A’.Назовем частные производные от функций g1,g2…gn. частными производными высшего порядка от функции f(M) и примем для каждого j (j=1,2,3…n)

(fx1)’xj=f’’x1xj , (f’x2)’xj=f’’x2xj,…, (f’xn)’xj=f’’xnxj или (f’xi)’xj=f’’xixj, где I и j= 1,2,3…n.

Эти производные разбиваются на две группы: вторые частные производные от f по переменным xi

f’’x²i= (f’xi)’xj, i=1,2,…n, j=1,2,…n.

и смешанные частные производные от f по переменным xi и xj (i≠j)

f’’xixj=(f’xi)’xj, i=1,2…n, j=1,2…n.

Число вторых частных производных функции f(M)равно n, а число смешанных частных производных – разности n²-n=n(n-1). При этом величина n² определяет общее число всех старших производных и совпадает с числом элементов квадратной матрицы порядка n. Элементы такой матрицы имеют индексы I и j, которые находятся во взаимно однозначном соответствии с координатными индексами xi, xj, определяющими порядок частной производной.