8.6.1. Скорость точки

Найдем значение скорости точки . Если за промежуток времениточка совершит вдоль дуги траектории перемещениеΔS(рис. 1.2), где одновременно ΔS– приращение координатыS, то численно средней скоростью точки за этот промежуток времени будети в пределе, найдем, что

или.

(16)

Таким образом, числовое значение скорости точки в данный момент времени равно первой производной от расстояния (криволинейной координаты) S этой точки по времени.

Значение скорости V можно также находить как отношение элементарного перемещенияdS точки к соответствующему промежутку времениdt. Так как всегдаdt>0, то знак скорости совпадает со знакомdS. Следовательно, когдаV>0, скорость направлена в сторону положительного отсчета расстоянияS, а когдаV<0, - в противоположную сторону. Таким образом, величинаVодновременно определяет и модуль скорости, и сторону, куда она направлена.

8.6.2. Ускорение точки

Установлено, что ускорение лежит в соприкасающейся плоскости, т. е. в плоско-

сти Mτn. Следовательно, проекция векторана бинормаль равна нулю (). Найдем проекциина две другие оси. Проектируя обе части равенствана осиМτиМnи обозначая символамиипроекции векторана эти оси получим:

.

(17)

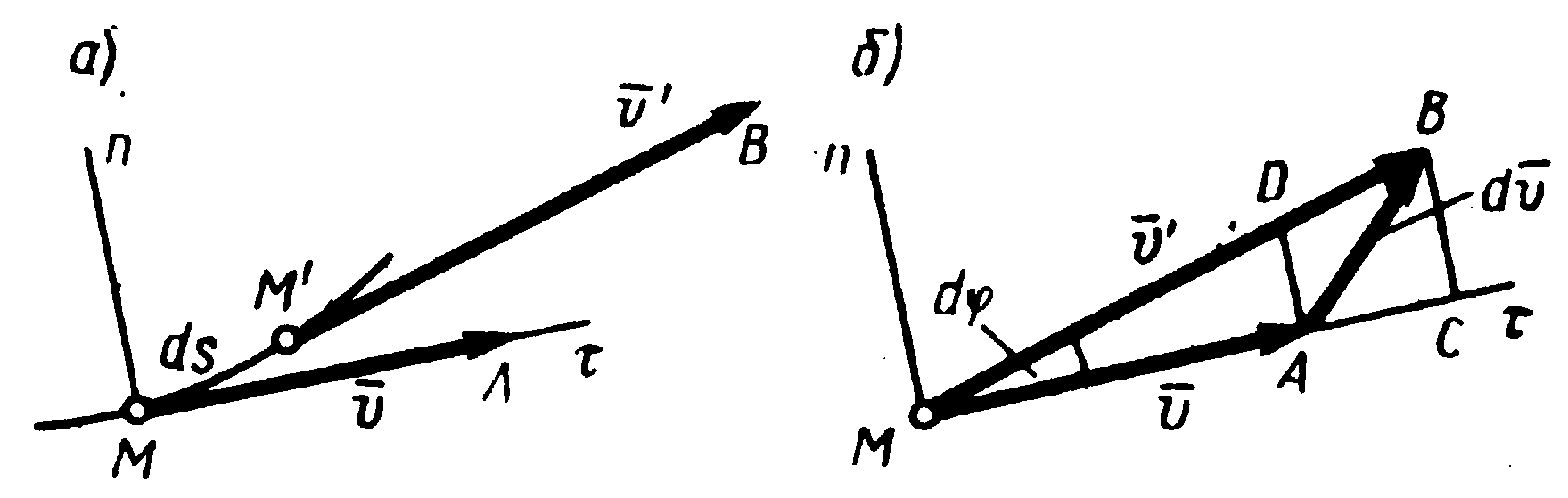
Рисунок 1.8

Вектор представляет собой разность между скоростями в двух соседних точкахМи(рис. 123,Т), т.е.. Отложим векторыиот общего начала (рис. 1.8), тогда, а фигуруАСВDпри бесконечно малом углеможно рассматривать как прямоугольник. Отсюда, гдеdV – элементарное приращение числового значения скорости. Далее, поскольку предел отношения дуги к хорде равен единице, можноАDрассматривать как элементарную дугу радиусаМА, размер которой определяется произведением радиуса на центральный угол. Тогда. Подставляя найденные значенияив формулы проекций, получим:

.

(18)

Угол между касательными к кривой в двух ее точках называется углом смежности, тогда- элементарный угол смежности. ОтношениекdS=, определяет кривизну кривой в точкеМ, а кривизнаkявляется величиной, обратной радиусу кривизны в этой точке, т.е.

.

(19)

Введем эту величину в равенство и преобразуем его, учтя, что, к виду

.

В результате окончательно получим:

.

(20)

Таким образом, проекция ускорения точки на касательную равна первой производной от числового значения скорости или второй производной от расстояния (криволинейной координаты) S по времени, а проекция ускорения на главную нормаль равна квадрату скорости, деленному на радиус кривизны траектории в данной точке кривой; проекция ускорения на бинормаль равна нулю.

Это одна из важных теорем кинематики. Величины иназываюткасательныминормальнымускорениями точки.

При движении точки Мв одной плоскости касательнаяМτ поворачивается вокруг бинормали Mbс угловой скоростью. Тогдадает еще одну формулу для вычисления:

.

Это значит, что нормальное ускорение равно произведению скорости точки на угловую скорость поворота касательной к траектории.

Кроме числового значения полного ускорения и его составляющих иважно знать их направление. Отложим вдоль касательнойМτи главной нормалиMnвекторыи(рис.1.9). При этом составляющаявсегда направлена в сторону вогнутости кривой, так как всегда>0, а составляющаяможет быть направлена или в положительном, или в отрицательном направлении осиМτв зависимости от знака.

Рисунок 1.9

Вектор изображается диагональю параллелограмма, построенного наи. Так как эти составляющие взаимно перпендикулярны, то модуль вектораи угол µ его отклонения от нормалиMnопределяется формулами:

,

,

(21)

где - ; приµ>0 векторотклонен от нормалиMnв сторону осиМτ,а приµ<0 – в противоположную сторону.

Таким образом, если движение точки задано естественным способом, то, зная траекторию (а, следовательно, и ее радиус кривизны в любой точке) и закон движения, т.е. зависимость , можно определить модуль и направление векторов скорости и ускорения в любой момент времени.