8.3. Вектор скорости точки

Одной из кинематических характеристик движения точки является векторная величина, называемая скоростью точки.

Скорость точки - это векторная величина, характеризующая быстроту и направление движения точки в данной системе отсчета.

Введем сначала понятие о средней скорости точки за какой-нибудь промежуток времени. Пусть движущаяся точка находится в момент временив положении(рис. 1.3), определяемом радиус-вектором, а в моментприходит в положение, определяемое вектором. Тогда перемещение точки за промежуток времениопределяется вектором, который будем называтьвектором перемещения точки.Этот вектор направлен по хорде, если точка движется криволинейно (рис. 1.3,а), и вдоль самой траектории, когда движение является прямолинейным (рис. 1.3,б).

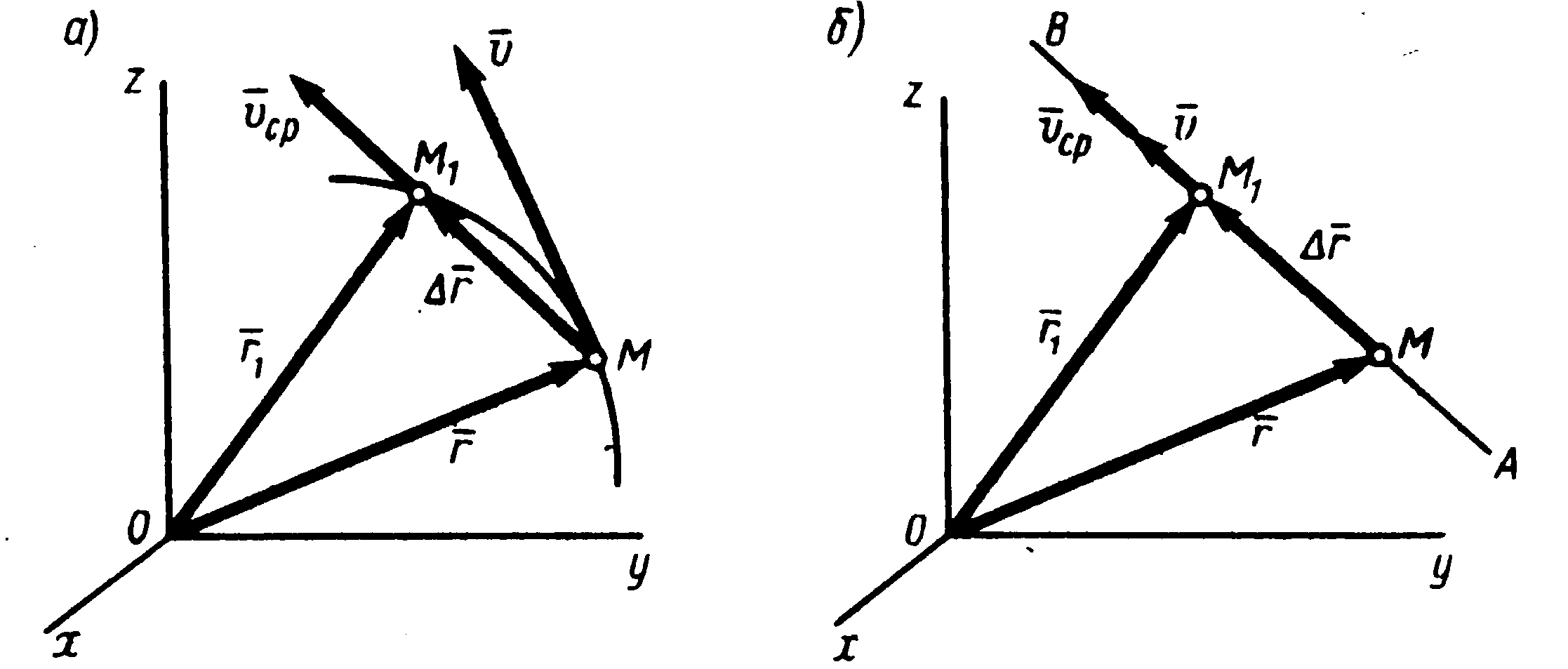
Рисунок 1.3

Из треугольника , видно, что, следовательно,

.

Отношение вектора перемещения точки к соответствующему промежутку времени дает векторную величину, называемую средней по модулю и направлению скоростью точки за промежуток времени :

.

(7)

Направлен вектор так же, как и вектор, т.е. при криволинейном движении вдоль хорды, в сторону движения точки, а при прямолинейном движении – вдоль самой траектории.

Очевидно, что чем меньше промежуток времени , тем величинабудет точнее характеризовать движение точки.

Поэтому скоростью точки в данный момент времениназывается векторная величина, к которой стремится скоростьпри стремлении промежутка временик нулю.

.

Предел отношения припредставляет собой первую производную от векторапо аргументу и обозначается, тогда

.

(8)

Итак, вектор скорости точки в данный момент времени равен первой производной от радиус-вектора точки по времени. Так как предельным направлением секущейявляется касательная, то вектор скорости в данный момент времени направлен по касательной к траектории точки в сторону движения.

Размерность скорости , т.е.. Единицы измерения.

8.4. Вектор ускорения точки

Ускорением точки называется векторная величина, характеризующая изменение с течением времени модуля и направления скорости.

Пусть в некоторый момент времени движущаяся точка находится в положениии имеет скорость(рис.1.4), а в момент времениприходит в точкуи имеет

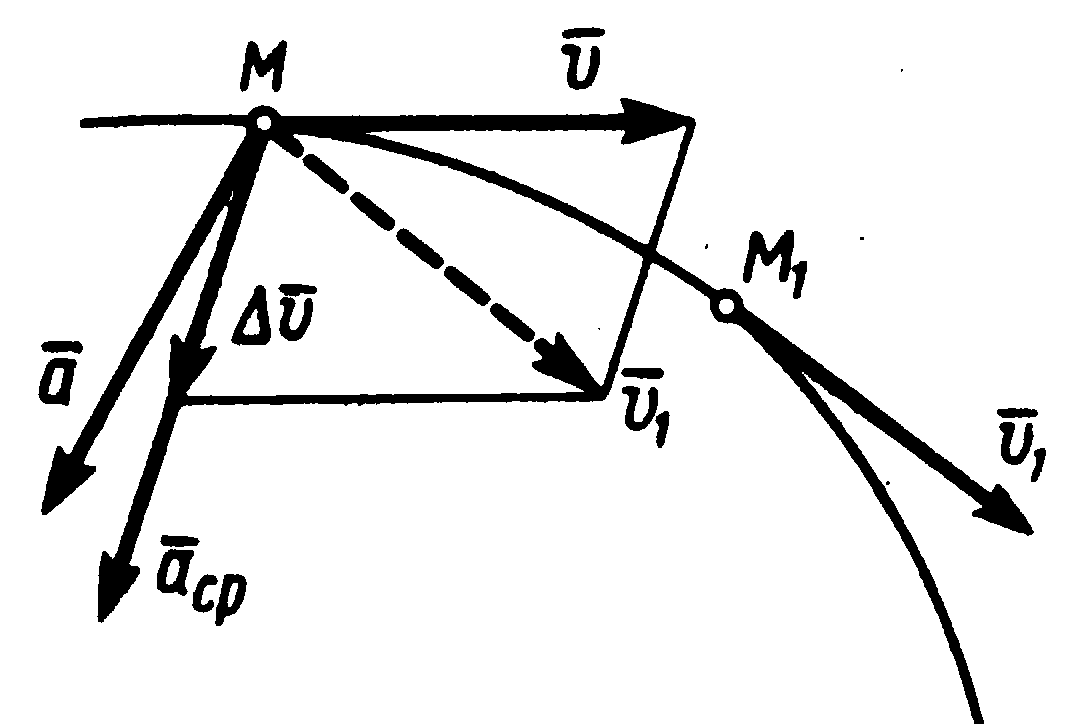
Рисунок 1.4

скорость . Тогда за промежуток временискорость изменится на. Для построения вектораотложим от точкивектор, равный, и построим параллелограмм, в котором диагональю будет, а одной из сторон. Тогда, очевидно,

вторая сторона и будет изображением вектора . Заметим, что векторвсегда направлен в сторону вогнутости траектории.

Отношение копределяет вектор среднего ускорения точки за промежуток времени.

.

(9)

Вектор среднего ускорения имеет то же направление, что и вектор , т.е. направлен в сторону вогнутости траектории. Тогда

или с учетом равенства (8),

.

(10)

Следовательно, вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиус-вектора точки по времени.

Размерность , т.е.. Единица измерения.

Вектор направлен, также как и вектор, лежит в плоскости этой кривой и направлен в сторону её вогнутости.