13.4. Сложение вращений вокруг пересекающихся осей

Пусть относительное движение тела представляет собой вращение с угловой ско-

ростью вокруг осиукрепленной на кривошипе2(рис. 6.5.а), а переносным является вращение кривошипа с угловой скоростьювокруг оси, которая с осьюпересекается в точкеО.

Рисунок 6.5

Очевидно, что в этом случае скорость точки О, как лежащей одновременно на обеих осях, будет равна нулю и результирующее движение тела является движением вокруг неподвижной точкиО. Тогда тело имеет в данный момент времени угловую скорость, направленную по мгновенной оси вращения, проходящей через точкуО. Схематически такой случай сложения вращений вокруг пересекающихся осей показан на рис. 6.5,б.

Чтобы определить , найдем скорость точкиМтелаи, определяя скорости точки как скорости вращающегося телаи полгая, запишем

так. Отсюда находим

,

(84)

т.е. при вращении тела вокруг двух осей, пересекающихся в точке О, результирующее движение будет мгновенным вращением вокруг оси Ос с угловой скоростью ,равной геометрической сумме . Мгновенная осьОс, вдоль которой направлен вектор, направлена по диагонали параллелограмма, построенного на векторахи(рис. 6.5,б).

С течением времени ось Осменяет свое положение, описывая коническую поверхность, вершина которой находится в точкеО.

13.5. Сложение поступательного и вращательного движений. Винтовое движение

Рассмотрим тело, вращающееся с угловой скоростью вокруг оси, жестко скрепленной с другим телом, имеющим поступательное движение со скоростью(рис. 6.6). В зависимости от значения углаαмежду векторамииздесь возможны три случая.

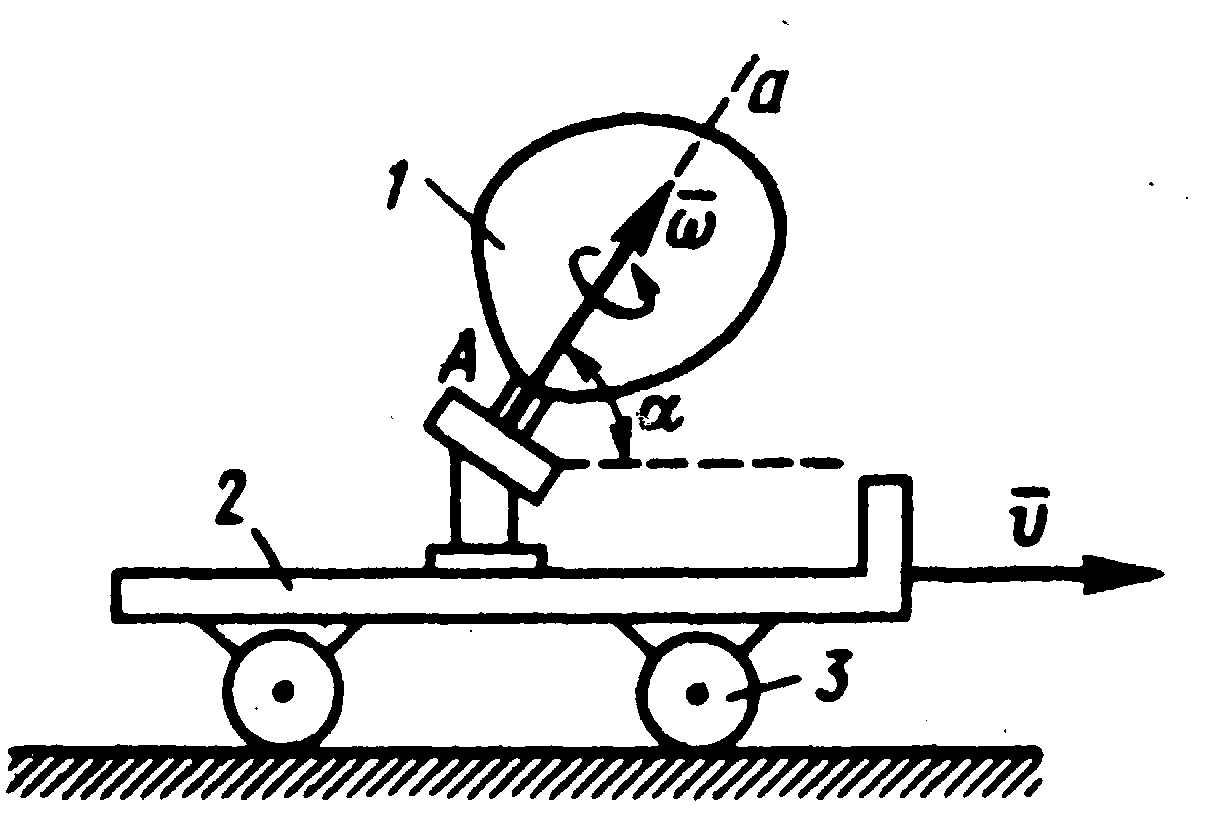
Рисунок 6.6

1. Скорость поступательного движения перпендикулярна оси вращения ().Пусть сложное движение тела слагается из вращательного движения вокруг осиАас угловой скоростьюи поступательного движения со скоростью, перпендикулярной(рис. 6.7). Легко видеть, что это плоскопараллельное движение. Тогда движение слагается из поступательного со скоростью(если точкуАсчитать полюсом) и вращательного вокруг осиАа, проходящей через полюс.

Рисунок 6.7

Вектор можно заменить парой угловых скоростей, беря их соответственно, а. При этом расстояниеАРопределится из равенства, откуда (учитывая, что)

.

(85)

Векторы при сложении дают нуль, и мы получаем, что движение тела в этом случае можно рассматривать как мгновенное вращение вокруг осис угловой скоростью, то есть точкаРявляется мгновенным центром скоростей. Здесь мы еще раз убеждаемся, что поворот тела вокруг осейАаипроисходит с одной и той же угловой скоростью, т.е. вращательная часть движения не зависит от выбора полюса.

2. Винтовое движение().

Ось Ааназывают осью винта (рис. 6.8). Когда векторыинаправлены в разные стороны, то при принятом нами правиле изображениявинт будет левым, если в одну сторону, - правым.

Рисунок 6.8

Расстояние, проходимое за время одного оборота любой точкой, лежащей на оси винта, называется шагом hвинта. Если величиныипостоянны, то шаг винта также будет постоянным. Обозначая время одного оборота черезТ, получаем в этом случаеи, откуда.

При постоянном шаге любая точка Мтела, не лежащая на оси вала, описываетвинтовую линию.

Скорость произвольной точки Мслагается из переносной скорости поступательного движения, и перпендикулярной ей относительной скорости, получаемой во вращательном движении и равной, следовательно

.

3. Скорость поступательного движения образует произвольный угол с осью вращения. Сложное движение, совершаемое телом в этом случае, представляет собой общий

случай движения свободного тела. Разложим вектор (рис. 6.9,а) на составляющие, направленную вдоль(), и, перпендикулярную (). Скоростьможно заменить парой угловых скоростейи, после чего векторыиможно отбросить. РасстояниеАСнайдем по формуле (78)

.

Тогда у тела остается вращение с угловой скоростью и поступательное движе-

Рисунок 6.9

ние со скоростью . Следовательно, распределение скоростей точек тела в данный момент времени будет таким же, как и при винтовом движении вокруг осиСсс угловой скоростью=и поступательной скоростью.

Проделанными операциями (рис. 6.9,б) мы перешли от полюса Ак полюсуС. Результат подтверждает, что в общем случае движения твердого тела угловая скорость при переносе полюса не изменяется, а меняется только поступательная скорость.

Так как при движении свободного твердого тела величины,иα будут все время изменяться, то будет непрерывно изменяться и положение осиСскоторую называют мгновенной винтовой осью. Таким образом, движение свободного тела можно еще рассматривать как слагающееся из серии мгновенных винтовых движений вокруг непрерывно изменяющихся винтовых осей.