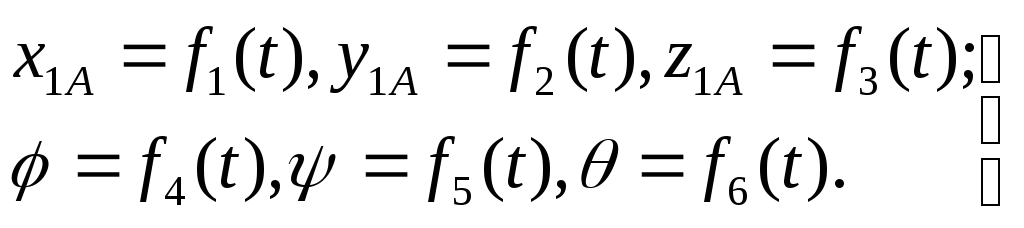11.3 Общий случай движения свободного твердого тела

Рассмотрим наиболее общий случай движения твердого тела, когда оно является свободным и может перемещаться как угодно по отношению к системе отсчета (рис. 4.8).

Рисунок 4.8

Установим вид уравнений, определяющих закон рассматриваемого движения. Выберем произвольную точку Атела в качестве полюса и проведем через неё оси, которые при движении тела будут перемешаться вместе с полюсом поступательно. Тогда положение тела в системе отсчетабудет известно, если будем знать положение полюсаА, т.е. его координаты, и положение тела по отношению к осям, определяемое, как и в случае рассмотрения движения тела, имеющего одну неподвижную точку, т.е. определяемую углами Эйлераφ;ψ;θ( рис.4.1). Следовательно, уравнения движения свободного твердого тела, позволяющие найти его положение по отношению к системе отсчетав любой момент времени, имеют вид

(64)

Первые три из уравнений определяют поступательную часть движения вместе с полюсом А. Последние три уравнения определяют сферическое движение тела вокруг точкиА, которое, как было установлено, представляет собой последовательность элементарных поворотов вокруг мгновенных осей вращения. Отсюда сделаем вывод, что в общем случае движение свободного твердого тела можно рассматривать как слагающееся из поступательного движения, при котором все точки тела движутся как произвольно выбранный полюсАсо скоростью, и из серии элементарных поворотов с угловой скоростьювокруг мгновенных осей вращения, проходящих через полюсА (рис. 4.9).

Соответственно этому основными характеристиками движения являются: скорость и ускорениеполюсаА, а также угловая скоростьи угловое ускорениевращения тела вокруг полюса. Если в качестве полюса принять другую точку тела, например, какую-нибудь

Рисунок 4.9

точку В(рис. 4.8) , то величиныив общем случае не будут равныи, а величиныиостанутся неизменными (как и для плоскопараллельного движения тела, эти величины от выбора полюса не зависят).

Скорость любой точки Мв рассматриваемом движении слагается из скоростиполюсаАи скорости, которую точкаМполучает при сферическом движении тела вокруг полюсаА. Скорость

.

(65)

Таким образом,

или.

(66)

Аналогично для ускорения любой точки Мнайдем

(67)

или

.

Глава 12. Сложное движение точки

12.1. Относительное, переносное и абсолютное движения.

12.2. Теорема о сложении скоростей.

12.3. Теорема о сложении ускорений (теорема Кориолиса).

12.1 Относительное, переносное и абсолютное движения

Сложное движение точки – это такое движение, при котором точка одновременно участвуют в двух или нескольких движения.

Рассмотрим точку М, движущуюся по отношению к подвижной системе отсчетаOxyz, которая в свою очередь как-то движется относительно другой системы отсчета, которая называется основной или условно подвижной (рис. 5.1). Каждая из этих систем отсчета связана, конечно, с определенным телом, на чертеже не показанным, Введем следующие определения.

Рисунок 5.1

1. Движение точки по отношению к подвижной системе отсчета (Oxyz)называется относительным движением.Траектория, описываемая точкой в относительном движении, называется относительной траекторией. Кинематические характеристики этого движения называются соответственноотносительной скоростьюиотносительным ускорением .

2. Движение, совершаемое подвижной системой отсчета Oxyz и всеми неизменно связанными с нею точками пространства по отношению к неподвижной системе, называетсяпереносным движением.Переносной скоростью точкиМ() называется скорость того пункта пространства, неизменно связанного с подвижной системойOxyz, через который в рассматриваемый момент времени проходит точкаМ. Аналогично определяется и переносное ускорение точкиМ().

3. Движение, совершаемое точкой Мпо отношению к неподвижной системе отсчета, называетсяабсолютнымилисложным. Траектория этого движения называется абсолютной траекторией. Кинематические характеристики этого движения будут называться соответственно абсолютной скоростью) и абсолютным ускорением ().

Определим соотношение рассмотренных кинематических параметров движения – скорости и ускорения.